Разбор задачи с IOI2012

Всем привет! В сентябре прошла международная олимпиада по программированию, IOI 2012. И мы, сборная России, на неё весьма успешно съездили, как вы могли видеть.

Я — Макс Ахмедов. Мне предложили поделиться с общественностью, что из себя представляют подобные соревнования и какие задачи нам приходится решать. Я расскажу о последней задаче второго тура «Jousting Tournament». Английский вариант условия можно найти здесь. К слову, это наиболее простая из трёх задач в тот день :-)

Легенда

В задаче идёт речь о церемонии обручения герцога Лодовико Сфорца, наместника Милана, и герцогини Беатриче д’Эсте, произошедшей в 1491. Организовывать празднества и управлять культурной программой герцог пригласил своего хорошего друга Леонардо да Винчи, который ему предложил, в частности, устроить шикарный рыцарский турнир.

И вот, к началу празднеств оказалось, что вовремя прибыли все рыцари, кроме одного, который опаздывает, но не настолько сильно, чтобы помешать проведению турнира. По случайному совпадению, этот рыцарь был фаворитом толпы, и все сражения с его участием пользовались большой популярностью. Леонардо знает расписание боёв турнира и то, как будут выбираться рыцари для участия в них, и он хочет слегка повлиять на ход турнира таким образом, чтобы рыцарь-фаворит поучаствовал в как можно большем количестве сражений. Так хитрый пиарщик Леонардо собирается увеличить значимость события.

Такая вот захватывающая история.

Формальное условие

Рыцарский турнир происходит следующим образом. В ряд стоит некоторое количество рыцарей. Перед каждым очередным сражением выходит судья и вызывает рыцарей, стоящих на позициях, образующих непрерывной отрезок, на поединок, в результате которого определяется победитель. Победитель возвращается на своё место, а проигравшие рыцари выбывают. После этого ряд рыцарей сдвигается, занимая пустые места. Более формально: в ряд стоят N рыцарей, судья называет два числа l и r, после этого рыцари, занимающие в порядке нумерации слева направо места с l-ого по r-ое, сражаются и из них в ряду остаётся только победитель. После этого происходят последующие сражения по такому же принципу до тех пор, пока не останется один рыцарь, который объявляется победителем турнира.

На данный момент все N — 1 рыцарей, кроме опаздывающего, уже заняли свои места в ряду. Леонардо имеет возможность поставить прибывшего фаворита на любое место в ряду, в том числе в начало или в конец. Порядок сражений и позиции рыцарей, в них участвующих, уже определены. Леонардо знает для каждого рыцаря значение его абстрактной “силы”, выражаемое целым числом от 0 до N — 1. В рамках этой задачи считается, что в сражении, в котором участвует определённые рыцари, в любом случае побеждает тот из них, который имеет наибольшее значение силы. Так сложилось, что на турнире все рыцари различны по силе, то есть в любом сражении победитель определяется однозначно исходя их знания их значений. Леонардо хочет добиться того, чтобы по итогам турнира количество сражений, в которых победил любимец толпы, было как можно большим, а из всех позиций, приводящих к такому исходу, он хочет выбрать самую левую. Обратите внимание: необязательно, чтобы наш рыцарь становился победителем всего турнира! Достаточно максимизировать количество сражений, из которых он вышел победителем.

Разберёмся на примере. Пусть в турнире участвуют 5 рыцарей. Пунктуальные рыцари, стоящие в ряд, имеют значения силы [1, 0, 2, 4], если смотреть слева направо. Как можно понять, опаздывающий рыцарь имеет значение силы 3. Пусть, например, турнир состоит из трёх раундов, которые характеризуются позициями (2, 4), (1, 2) и (1, 2). Поясним, что это значит.

• В первом сражаются рыцари, стоящие на местах со второго слева по четвёртое слева.
• Во втором из оставшихся рыцарей сразятся те двое, что стоят на первом слева и втором слева местах.
• В последнем раунде встретятся оставшиеся два рыцаря, занимающие первое слева и второе слева места; после этого снова сразятся рыцари на первом и втором месте.

Такой турнир можно более наглядно отобразить в виде дерева:

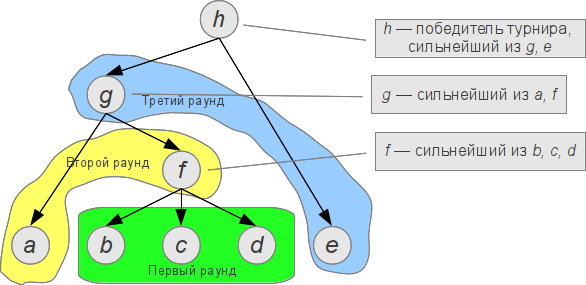
Далее, к слову, мы ещё вернёмся к подобным деревьям.

Поймём, как будет выглядеть картина турнира, если, например, Леонардо поставит фаворита слева от всех остальных рыцарей. Изначально значения силы рыцарей выглядят слева направо как [3, 1, 0, 2, 4].

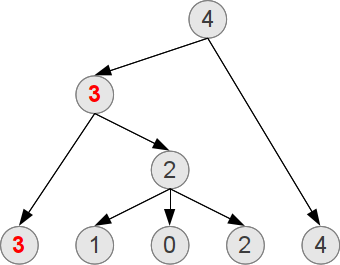
• В первом раунде сразятся рыцари, имеющие силу 1, 0 и 2. Победителем выйдет рыцарь силой 2, он вернётся на своё место, и ряд будет выглядеть как [3, 2, 4].
• Во втором раунде сразится наш фаворит силой 3 и рыцарь силой 2. Любимец толпы выйдет победителем, он вернётся, и ряд будет выглядеть как [3, 4].
• В последнем раунде наш фаворит проиграет рыцарю силой 4, который станет победителем турнира.

Таким образом, наш рыцарь выиграет всего лишь один поединок, до того как выбыть. Лучшим решением было бы поставить его на позицию между рыцарями рангами 1 и 0, образовав ряд [1, 3, 0, 2, 4].

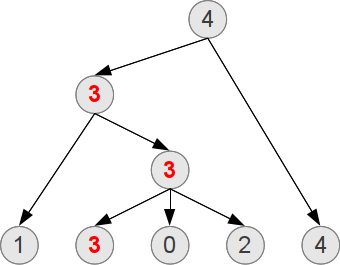
• В первом раунде он поучаствует в сражении с рыцарями силами 0 и 2, из которого выйдет победителем. Ряд рыцарей теперь имеет вид [1, 3, 4].
• Во втором раунде он же сразится с рыцарем силой 1, которого победит.
• В третьем раунде он так же проигрывает победителю турнира силой 4.

В итоге фаворит выигрывает два поединка.

Большее количество сражений он выиграть не может, так как он уже выиграл все раунды, кроме одного, а победить во всех он не может, потому что есть рыцарь (имеющий ранг 4) сильнее его, который гарантированно станет победителем турнира. Значит, позиция между первыми двумя рыцарями – это та самая, требуемая Леонардо, которая является ответом к задаче.

Количество баллов, которое получит программа, зависит от эффективности решения. Если оно работает достаточно быстро, чтобы получать за одну секунду правильный ответ в ситуациях, где количество рыцарей не превышает 500, то решение получит 17 баллов из 100. Если оно успевает посчитать правильный ответ при количестве рыцарей, достигающем 5000, то оно будет оценено в 49 баллов. Для получения полного балла решение должно успевать обрабатывать турниры, включающие до ста тысяч рыцарей. В нашей сборной все четыре человека написали решения, получающие 100 баллов — задача оказалась самой простой на туре.

Решение в лоб

Простейшим решением к задаче будет явно проверить каждую из N возможных позиций для опаздывающего рыцаря и найти из них наиболее выгодную. Единственным техническим моментом в решении будет симулирование турнира при данном изначальном расположении рыцарей. Можно делать это совершенно наивно: например, поддерживать ряд рыцарей в списке слева направо и в каждом очередном раунде выделять сражающихся рыцарей, находить из них самого сильного, ставить его обратно, и сдвигать рыцарей, заполняя пустые места.

Такое решение должно проходить первую группу тестов, в которых количество рыцарей не превосходит пятисот. Давайте оценим, сколько оно будет работать, посчитав порядок количества операций, выполняемых программой. В каждом раунде нам необходимо в худшем случае сдвигать почти всех рыцарей левее, заполняя пустые места, то есть один раунд программа в худшем случае обрабатывает за количество операций, пропорциональное длине ряда, который в среднем состоит из, грубо говоря, N / 2 рыцарей. Раундов в турнире в худшем же случае может быть аж N — 1, а нам еще нужно просимулировать целых N возможных турниров – для всех возможных позиций опоздавшего рыцаря. Получается зависимость N^3 / 2 для количества простых операций, выполняемых программой от количества рыцарей N.

К слову, современные компьютеры успевают выполнить порядка 400-500 миллионов простых операций за секунду. Мы оценили сложность нашего решения для N = 500 как около 62 миллионов простых операций, поэтому можно рассчитывать на то, что оно с запасом уложится в ограничение по времени. И действительно, написав это решение, можно получить заслуженные семнадцать баллов – это полезно хотя бы потому, что такое решение может стать хорошим подспорьем при дальнейших отладке и тестировании задачи, благо реализуется совсем просто.

We need to go deeper

Для того чтобы решение работало не более секунды на тестах с 5000 рыцарей, кубическая сложность алгоритма уже никак не подходит – нужно снижать оценку сложности хотя бы до пропорциональной квадрату N. В таких случаях часто употребляют O-большое терминологию: речь идет об алгоритме сложностью O(N^2).

Нам нужно убрать один их трех множителей N в оценке сложности выше. Как избавляться от внешнего – перебора позиции для опоздавшего рыцаря – пока не очень понятно. Значит, давайте увеличивать эффективность симуляции турнира. От количества раундов нам, казалось бы, никуда не уйти – стало быть, надо сделать более эффективным выполнение одного сражения. У нас есть очень неэффективный кусок в сдвигании всех рыцарей для заполнения пустых мест: так как массив лежит в памяти неделимым фрагментом и мы хотим быстро переходить к рыцарю по его позиции, от этого никуда не уйти. Нам нужно как-то изменить структуру их хранения.

Одним из решений было бы использование вместо массива рыцарей какой-либо структуры, позволяющей вырезать отрезки за более короткое время. Но этот путь очень сомнительный, потому что большинство таких структур работает не быстрее, чем за время O(log N), а сложность работы O(N^2 log N) – очень опасна: 300 миллионов операций совершенно не гарантируют, что решение войдет во временные ограничения.

Налицо факт, что мы делаем слишком много лишних операций – зачем-то поддерживаем положения рыцарей в явном виде. Если вспомнить о такой штуке, как дерево турнира, то становится ясно, как ее использовать для быстрого проведения всех сражений. Если мы должны провести раунд, соответствующий какой-то вершине, то нам достаточно провести раунды, соответствующие дочерним вершинам, а потом выбрать из победителей этих раундов самого сильного. Это делается, например, во время обхода дерева турнира в глубину. Таким образом, при наличии дерева турнира мы можем провести все сражения за линейное время O(N). Снаружи у нас по-прежнему стоит перебор позиции, куда мы ставим нашего фаворита, тоже имеющий сложность O(N). Значит, собственно нахождение ответа при данном дереве мы умеем выполнять за O(N^2).

Осталось только научиться это дерево строить. Нам достаточно его построить один раз хоть за квадратичное время, чтобы потом использовать. Это можно делать по аналогии с тем, как мы в наивном решении проводили раунды: будем вместо значений силы рыцарей хранить в ряду вершины в дереве турнира, соответствующие рыцарям-победителям на этих местах. С каждым раундом будем выделять подотрезок, на котором стоят рыцари-вершины, участвующие в этом раунде, и ставить вместо этого подотрезка новую, родительскую для всех, вершину.

Таким образом, у нас вышло решение, требующее O(N^2) памяти на построение дерева турнира и O(N^2) на нахождение по нему ответа. Такое решение при N <= 5000 должно с запасом заходить по времени и получать 49 баллов.

Прокачиваем решение до полного балла

Давайте дальше улучшать решение. Построение дерева можно оптимизировать по времени, если вместо массива хранить вершины дерева турнира в какой-нибудь структуре данных, умеющей быстро вырезать подотрезок (быстрее, чем за O(N), как это можно сделать в массиве). Примером такой удобной структуры данных является декартово дерево по неявному ключу, о котором когда-то речь шла на хабре в том числе, и о котором можно почитать, например, здесь. В итоге, реализация построения дерева турнира останется почти прежней, за тем исключением, что поменяется представление рыцарей-вершин в ряду и способ работы с ними. Тем самым, первая часть решения оптимизирована до O(N log N).

Чтобы оптимизировать вторую часть, нужно понять, чтоперемещение нашего одного-единственного фаворита на результаты турнира влияет, в принципе, совсем не сильно. Например, то, где изначально стоит опоздавший, никоим образом не изменит победителя всего турнира – это в любом случае будет рыцарь с самой большой силой.

Давайте дальше рассуждать – вот кто вообще оказывается в определённой вершине дерева турнира как победитель? Достаточно очевидно, что это рыцарь, являющийся самым сильным в поддереве, соответствующем этой вершине. Это – очень полезное соображение, оно нам позволяет понять, например, когда наш фаворит может теоретически оказаться как победитель в какой-нибудь вершине: для этого необходимо и достаточно, чтобы в этом поддереве не было рыцаря сильнее его. А что такое поддерево какой-то вершины? Это отрезок ряда, в котором уже стоят пунктуальные рыцари – самого сильного рыцаря на нём мы можем найти, например, с помощью такой структуры данных, как дерево отрезков.

Значит, для каждой вершины дерева турнира мы можем определить, может ли наш фаворит в ней оказаться. А если он может в ней оказаться, то нам выгоднее всего поставить его на такую позицию, чтобы путь до неё в этом дереве был как можно длиннее: каждая вершина на пути – это какое-то сражение, в котором фаворит побывал, а нам ровно это количество сражений и надо максимизировать по условию задачи. Значит, осталось только из всех доступных нашему фавориту вершин выбрать ту из них, которая содержит максимально глубокий лист (то есть вершину дерева, не имеющую «детей» – эта вершина соответствует какой-то позиции для рыцаря), и выбрать этот лист в качестве ответа.

Тем самым вторая часть решения тоже оптимизировалась до O(N log N). Для N <= 100000 решение с такой сложностью, как правило, заходит в ограничение по времени – эта задача не является исключением. И действительно, реализовав такое (за незначительными отклонениями) решение, мы вчетвером получили полный балл.

Вот такие пирожки

Чем-то из такой оперы на наших олимпиадах мы и занимаемся — это типичный пример многоходовой, серьёзной задачи с международной олимпиады с различными путями решения и множеством логических кирпичиков. Надеюсь, стало чуть-чуть более ясно, чего мы такое программируем, и за что потом получаем медальки :-) До встречи!

Автор: Zlobober