Введение
Представляем вторую статью в серии, задуманной, чтобы помочь быстро разобраться в технологии глубокого обучения; мы будем двигаться от базовых принципов к нетривиальным особенностям с целью получить достойную производительность на двух наборах данных: MNIST (классификация рукописных цифр) и CIFAR-10 (классификация небольших изображений по десяти классам: самолет, автомобиль, птица, кошка, олень, собака, лягушка, лошадь, корабль и грузовик).


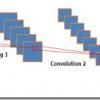
На прошлом уроке мы ввели базовые понятия глубокого обучения и показали, как можно быстро смоделировать модели нейронных сетей с помощью фреймворка Keras. Напоследок многослойный перцептрон (MLP), содержащий два слоя, применили к MNIST, достигнув уровня точности 98.2%, причем это значение достаточно просто улучшить. Но все же полносвязный перцептрон обычно не выбирают для задач, связанных с распознаванием изображений — в этом случае намного чаще пользуются преимуществами сверточных нейронных сетей (Convolutional Neural Networks, CNN). Пройдя этот курс, вы будете понимать принцип работы и научитесь строить CNN в Keras, достигая хорошего уровня точности на CIFAR-10.
Эта статья предполагает знакомство с предыдущей статьей цикла.
Обработка изображений
Упомянутый выше многослойный перцептрон представляет собой самую мощную и возможных нейронных сетей прямого распространения. Он состоит из нескольких слоем, где каждый слой организован таким образом, что каждый нейрон в одном слое получает свою копию всех выходных данных предыдущего слоя. Эта модель идеально подходит для определенных типов задач, например, обучение на ограниченном количество более или менее неструктурированных параметров.
Тем не менее, посмотрим, что происходит с количеством параметров (весов) в такой модели, когда ей на вход поступают необработанные данные. Например, CIFAR-10 содержит 32 x 32 x 3 цветных изображений, и если мы будем считать каждый канал каждого пикселя независимым входным параметром для MLP, каждый нейрон в первом скрытом слое добавляет к модели около 3000 новых параметров! И с ростом размера изображений ситуация быстро выходит из-под контроля, причем происходит это намного раньше, чем изображения достигают того размера, с которыми обычно работают пользователи реальных приложений.
Одно из популярных решений — понижать разрешение изображений до той степени, когда MLP становится применим. Тем не менее, когда мы просто понижаем разрешение, мы рискуем потерять большое количество информации, и было бы здорово, если бы можно было осуществлять полезную первичную обработку информации еще до применения понижения качества, не вызывая при этом взрывного роста количества параметров модели.
Свертка функций
Оказывается, существует весьма эффективный способ решения этой задачи, который обращает в нашу пользу саму структуру изображения: предполагается, что пиксели, находящиеся близко друг к другу, теснее “взаимодействуют” при формировании интересующего нас признака, чем пиксели, расположенные в противоположных углах. Кроме того, если в процессе классификации изображения небольшая черта считается очень важной, не будет иметь значения, на каком участке изображения эта черта обнаружена.
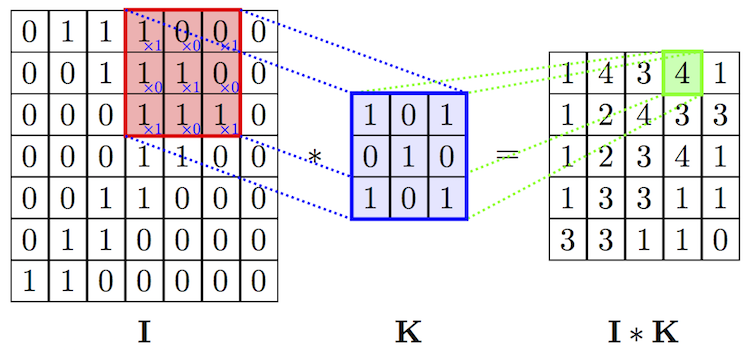
Введем понятие оператора свертки. Имея двумерное изображение I и небольшую матрицу K размерности 

На самом деле, точное определение предполагает, что матрица ядра будет транспонирована, но для задач машинного обучения не важно, выполнялась эта операция или нет.
На рисунках ниже схематически изображена вышеуказанная формула, а также представлен результат применения операции свертки (с двумя разными ядрами) к изображению с целью выделить контуры объекта.

Сверточные и субдискретизирующие слои
Оператор свертки составляет основу сверточного слоя (convolutional layer) в CNN. Слой состоит из определенного количества ядер 



Обратите внимание, что так как все, что мы здесь делаем — это сложение и масштабирование входных пикселей, ядра можно получить из имеющейся обучающей выборки методом градиентного спуска, аналогично вычислению весов в многослойном перцептроне (MLP). На самом деле MLP мог бы в совершенстве справиться с функциями сверточного слоя, но времени на обучение (как и обучающих данных) потребовалось бы намного больше.
Заметим также, что оператор свертки вовсе не ограничен двухмерными данными: большинство фреймворков глубокого обучения (включая Keras) предоставляют слои для одномерной или трехмерной свертки прямо “из коробки”.
Стоит также отметить, что хотя сверточный слой сокращает количество параметров по сравнению с полносвязным слоем, он использует больше гиперпараметров — параметров, выбираемых до начала обучения.
В частности, выбираются следующие гиперпараметры:
- Глубина (depth) — сколько ядер и коэффициентов смещения будет задействовано в одном слое;
- Высота (height) и ширина (width) каждого ядра;
- Шаг (stride) — на сколько смещается ядро на каждом шаге при вычислении следующего пикселя результирующего изображения. Обычно его принимают равным 1, и чем больше его значение, тем меньше размер выходного изображения;
- Отступ (padding): заметим, что свертка любым ядром размерности более, чем 1х1 уменьшит размер выходного изображения. Так как в общем случае желательно сохранять размер исходного изображения, рисунок дополняется нулями по краям.
Как читатель уже догадался, операции свертки — не единственные операции в CNN (хотя существуют многообещающие исследования на тему “чисто-сверхточных” сетей); они чаще применяются для выделения наиболее полезных признаков перед субдискретизацией (downsampling) и последующей обработкой с помощью MLP.
Популярный способ субдискретизации изображения — слой подвыборки (также называемый слоем субдискретизации, по-английски downsampling или pooling layer), который получает на вход маленькие отдельные фрагменты изображения (обычно 2х2) и объединяет каждый фрагмент в одно значение. Существует несколько возможных способов агрегации, наиболее часто из четырех пикселей выбирается максимальный. Этот способ схематически изображен ниже.
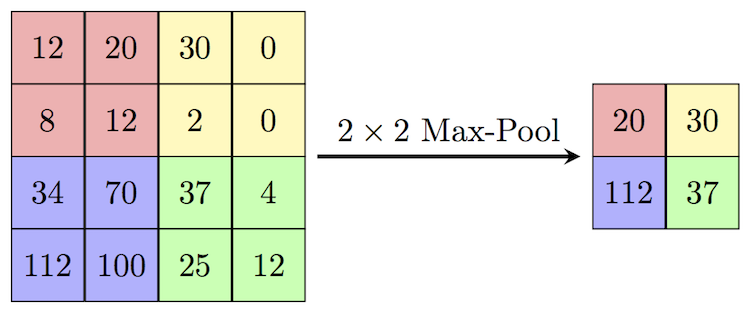
Итого: обычная CNN
Теперь, когда у нас есть все строительные блоки, давайте рассмотрим, как выглядит обычная CNN целиком!
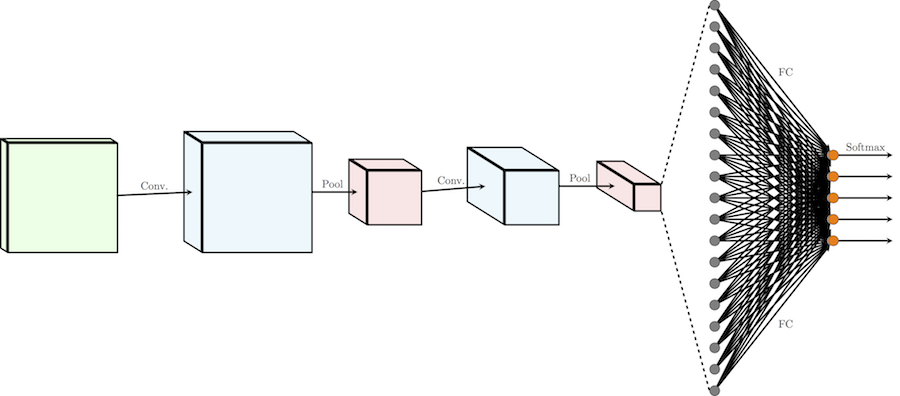
Обычную архитектуру CNN для распределения изображений по k классам можно разделить на две части: цепочка чередующихся слоев свертки/подвыборки 
Один проход 
Softmax и перекрестная энтропия более подробно рассмотрены на предыдущем уроке. Напомним, что функция softmax превращает вектор действительных чисел в вектор вероятностей (неотрицательные действительные числа, не превышающие 1). В нашем контексте выходные значения являются вероятностями попадания изображения в определённый класс. Минимизация потерь перекрестной энтропии обеспечивает уверенность в определении принадлежности изображения определенному классу, не принимая во внимание вероятность остальных классов, таким образом, для вероятностных задач softmax предпочтительней, чем, например, метод квадратичной ошибки.
Отступление: переобучение, регуляризация и dropout
Впервые (и, надеюсь, только однажды) я обращу ваше внимание на тему, на первый взгляд, не относящуюся к предмету. Она касается очень важного подводного камня глубокого обучения — проблемы переобучения (overfitting). Хотя эта тема будет основной в следующей статье цикла, отрицательный эффект переобучения заметно проявляется на сетях, подобных той, что мы собираемся построить, а значит, необходимо найти способ защититься от этого явления прежде, чем мы пойдем дальше. К счастью, существует очень простой метод, который мы и применим.
Переобучение — это излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению. Другими словами, наша модель могла выучить обучающее множество (вместе с шумом, который в нем присутствует), но она не смогла распознать скрытые процессы, которые это множество породили. В качестве примера рассмотрим задачу аппроксимации синусоиды с аддитивным шумом.
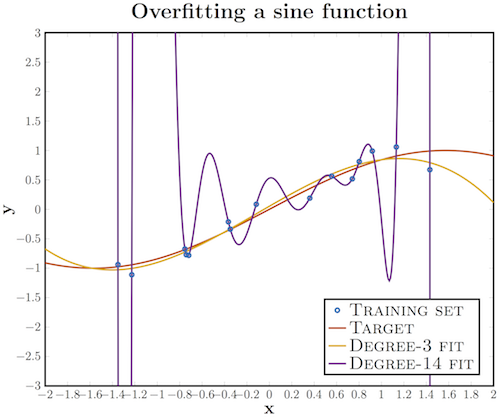
У нас есть обучающее множество (синие кружки), полученное из исходной кривой синуса, с некоторым количеством шума. Если мы приложим к этим данным график многочлена третьей степени, мы получим хорошую аппроксимацию исходной кривой. Кто-то возразит, что многочлен 14-й степени подошел бы лучше; действительно, так как у нас есть 15 точек, такая аппроксимация идеально описала бы обучающую выборку. Тем не менее, в этом случае введение дополнительных параметров в модель приводит к катастрофическим результатам: из-за того, что наша аппроксимация учитывает шумы, она не совпадает с исходной кривой нигде, кроме обучающих точек.
У глубоких сверточных нейронных сетей масса разнообразных параметров, особенно это касается полносвязных слоев. Переобучение может проявить себя в следующей форме: если у нас недостаточно обучающих примеров, маленькая группа нейронов может стать ответственной за большинство вычислений, а остальные нейроны станут избыточны; или наоборот, некоторые нейроны могут нанести ущерб производительности, при этом другие нейроны из их слоя не будут заниматься ничем, кроме исправления их ошибок.
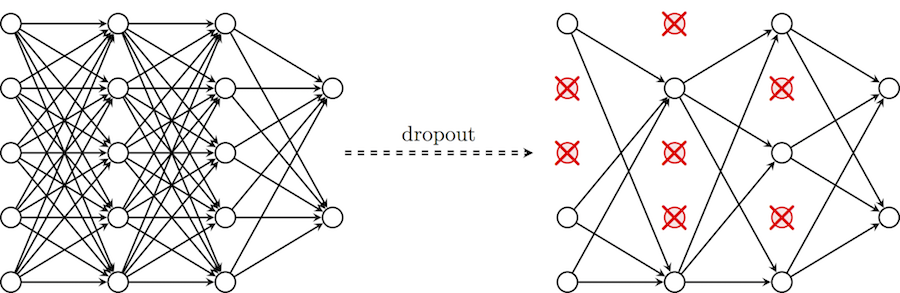
Чтобы помочь нашей сети не утратить способности к обобщению в этих обстоятельствах, мы вводим приемы регуляризации: вместо сокращения количества параметров, мы накладываем ограничения на параметры модели во время обучения, не позволяя нейронам изучать шум обучающих данных. Здесь я опишу прием dropout, который сначала может показаться “черной магией”, но на деле помогает исключить ситуации, описанные выше. В частности, dropout с параметром p за одну итерацию обучения проходит по всем нейронам определенного слоя и с вероятностью p полностью исключает их из сети на время итерации. Это заставит сеть обрабатывать ошибки и не полагаться на существование определенного нейрона (или группы нейронов), а полагаться на “единое мнение” (consensus) нейронов внутри одного слоя. Это довольно простой метод, который эффективно борется с проблемой переобучения сам, без необходимости вводить другие регуляризаторы. Схема ниже иллюстрирует данный метод.
Применение глубокой CNN к CIFAR-10
В качестве практической части построим глубокую сверточную нейронную сеть и применим ее к классификации изображений из набора CIFAR-10.
Импорты те же, что и в прошлый раз, за исключением того что мы используем большее разнообразие слоев:
from keras.datasets import cifar10 # subroutines for fetching the CIFAR-10 dataset
from keras.models import Model # basic class for specifying and training a neural network
from keras.layers import Input, Convolution2D, MaxPooling2D, Dense, Dropout, Flatten
from keras.utils import np_utils # utilities for one-hot encoding of ground truth values
import numpy as npUsing Theano backend.Как уже говорилось, обычно CNN использует больше гиперпараметров, чем MLP. В этом руководстве мы все еще будем использовать заранее известные “хорошие” значения, но не будем забывать, что в последующей лекции я расскажу, как их правильно выбирать.
Зададим следующие гиперпараметры:
- batch_size — количество обучающих образцов, обрабатываемых одновременно за одну итерацию алгоритма градиентного спуска;
- num_epochs — количество итераций обучающего алгоритма по всему обучающему множеству;
- kernel_size — размер ядра в сверточных слоях;
- pool_size — размер подвыборки в слоях подвыборки;
- сonv_depth — количество ядер в сверточных слоях;
- drop_prob (dropout probability) — мы будем применять dropout после каждого слоя подвыборки, а также после полносвязного слоя;
- hidden_size — количество нейронов в полносвязном слое MLP.
NB: я задал 200 итераций, что может занять слишком много времени, если в вашем распоряжении нет графического процессора (в этом случае узким местом будут сверточные слои). Если вы собираетесь обучать сеть на CPU, стоит сократить количество итераций и/или ядер.
batch_size = 32 # in each iteration, we consider 32 training examples at once
num_epochs = 200 # we iterate 200 times over the entire training set
kernel_size = 3 # we will use 3x3 kernels throughout
pool_size = 2 # we will use 2x2 pooling throughout
conv_depth_1 = 32 # we will initially have 32 kernels per conv. layer...
conv_depth_2 = 64 # ...switching to 64 after the first pooling layer
drop_prob_1 = 0.25 # dropout after pooling with probability 0.25
drop_prob_2 = 0.5 # dropout in the FC layer with probability 0.5
hidden_size = 512 # the FC layer will have 512 neuronsЗагрузка и первичная обработка CIFAR-10 осуществляется ровно так же, как и загрузка и обработка MNIST, где Keras выполняет все автоматически. Единственное отличие состоит в том, что теперь мы не рассматриваем каждый пиксель как независимое входное значение, и поэтому мы не переносим изображение в одномерное пространство. Мы снова преобразуем интенсивность пикселей так, чтобы она попадала в отрезок [0,1] и используем прямое кодирование для выходных значений.
Тем не менее, в этот раз этот этап будет выполнен для более общего случая, что позволит проще приспосабливаться к новым наборам данных: размер будет не жестко задан, а вычислен из размера набора данных, количество классов будет определено по количеству уникальных меток в обучающем множестве, а нормализация будет выполнена путем деления всех элементов на максимальное значение обучающего множества.
NB: мы также разделим тестовое множество на максимальное значение обучающего множества, потому что нашим алгоритмам не позволено видеть тестовые данные до того как завершится процесс обучения, и поэтому мы не можем вычислять на их основе никакие статистические метрики кроме как применения тех же трансформаций, что происходили с обучающим множеством.
(X_train, y_train), (X_test, y_test) = cifar10.load_data() # fetch CIFAR-10 data
num_train, depth, height, width = X_train.shape # there are 50000 training examples in CIFAR-10
num_test = X_test.shape[0] # there are 10000 test examples in CIFAR-10
num_classes = np.unique(y_train).shape[0] # there are 10 image classes
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= np.max(X_train) # Normalise data to [0, 1] range
X_test /= np.max(X_train) # Normalise data to [0, 1] range
Y_train = np_utils.to_categorical(y_train, num_classes) # One-hot encode the labels
Y_test = np_utils.to_categorical(y_test, num_classes) # One-hot encode the labels
Настало время моделирования! Наша сеть будет состоять из четырех слоев Convolution_2D и слоев MaxPooling2D после второй и четвертой сверток. После первого слоя подвыборки мы удваиваем количество ядер (вместе с описанным выше принципом принесения высоты и ширины в жертву глубине). После этого выходное изображение слоя подвыборки трансформируется в одномерный вектор (слоем Flatten) и проходит два полносвязных слоя (Dense). На всех слоях, кроме выходного полносвязного слоя, используется функция активации ReLU, последний же слой использует softmax.
Для регуляризации нашей модели после каждого слоя подвыборки и первого полносвязного слоя применяется слой Dropout. Здесь Keras также выделяется на фоне остальных фреймворков: в нем есть внутренний флаг, который автоматически включает и выключает dropout, в зависимости от того, находится модель в фазе обучения или тестирования.
В остальном спецификация нашей модели совпадает с нашими предыдущими настройками для MNIST:
- Мы используем перекрестную энтропию в качестве функции потерь;
- Мы используем оптимизатор Адама для градиентного спуска;
- Мы измеряем точность модели (так как исходные данные распределены по классам равномерно)*;
- Мы оставляем 10% данных для последующей валидации.
*Чтобы понять, почему точность не подойдет для случаев, когда распределение данных по классам неравномерно, рассмотрим предельный случай, когда 90% тестовых данных принадлежит классу x (например, в задаче диагностики у пациентов редкого заболевания). В этом случае классификатор, который просто выводит x, достигает значительной точности 90%, хотя на деле не выполняет ни обучения, ни обобщения.
inp = Input(shape=(depth, height, width)) # N.B. depth goes first in Keras!
# Conv [32] -> Conv [32] -> Pool (with dropout on the pooling layer)
conv_1 = Convolution2D(conv_depth_1, kernel_size, kernel_size, border_mode='same', activation='relu')(inp)
conv_2 = Convolution2D(conv_depth_1, kernel_size, kernel_size, border_mode='same', activation='relu')(conv_1)
pool_1 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_2)
drop_1 = Dropout(drop_prob_1)(pool_1)
# Conv [64] -> Conv [64] -> Pool (with dropout on the pooling layer)
conv_3 = Convolution2D(conv_depth_2, kernel_size, kernel_size, border_mode='same', activation='relu')(drop_1)
conv_4 = Convolution2D(conv_depth_2, kernel_size, kernel_size, border_mode='same', activation='relu')(conv_3)
pool_2 = MaxPooling2D(pool_size=(pool_size, pool_size))(conv_4)
drop_2 = Dropout(drop_prob_1)(pool_2)
# Now flatten to 1D, apply FC -> ReLU (with dropout) -> softmax
flat = Flatten()(drop_2)
hidden = Dense(hidden_size, activation='relu')(flat)
drop_3 = Dropout(drop_prob_2)(hidden)
out = Dense(num_classes, activation='softmax')(drop_3)
model = Model(input=inp, output=out) # To define a model, just specify its input and output layers
model.compile(loss='categorical_crossentropy', # using the cross-entropy loss function
optimizer='adam', # using the Adam optimiser
metrics=['accuracy']) # reporting the accuracy
model.fit(X_train, Y_train, # Train the model using the training set...
batch_size=batch_size, nb_epoch=num_epochs,
verbose=1, validation_split=0.1) # ...holding out 10% of the data for validation
model.evaluate(X_test, Y_test, verbose=1) # Evaluate the trained model on the test set!Train on 45000 samples, validate on 5000 samples
Epoch 1/200
45000/45000 [==============================] - 9s - loss: 1.5435 - acc: 0.4359 - val_loss: 1.2057 - val_acc: 0.5672
Epoch 2/200
45000/45000 [==============================] - 9s - loss: 1.1544 - acc: 0.5886 - val_loss: 0.9679 - val_acc: 0.6566
Epoch 3/200
45000/45000 [==============================] - 8s - loss: 1.0114 - acc: 0.6418 - val_loss: 0.8807 - val_acc: 0.6870
Epoch 4/200
45000/45000 [==============================] - 8s - loss: 0.9183 - acc: 0.6766 - val_loss: 0.7945 - val_acc: 0.7224
Epoch 5/200
45000/45000 [==============================] - 9s - loss: 0.8507 - acc: 0.6994 - val_loss: 0.7531 - val_acc: 0.7400
Epoch 6/200
45000/45000 [==============================] - 9s - loss: 0.8064 - acc: 0.7161 - val_loss: 0.7174 - val_acc: 0.7496
Epoch 7/200
45000/45000 [==============================] - 9s - loss: 0.7561 - acc: 0.7331 - val_loss: 0.7116 - val_acc: 0.7622
Epoch 8/200
45000/45000 [==============================] - 9s - loss: 0.7156 - acc: 0.7476 - val_loss: 0.6773 - val_acc: 0.7670
Epoch 9/200
45000/45000 [==============================] - 9s - loss: 0.6833 - acc: 0.7594 - val_loss: 0.6855 - val_acc: 0.7644
Epoch 10/200
45000/45000 [==============================] - 9s - loss: 0.6580 - acc: 0.7656 - val_loss: 0.6608 - val_acc: 0.7748
Epoch 11/200
45000/45000 [==============================] - 9s - loss: 0.6308 - acc: 0.7750 - val_loss: 0.6854 - val_acc: 0.7730
Epoch 12/200
45000/45000 [==============================] - 9s - loss: 0.6035 - acc: 0.7832 - val_loss: 0.6853 - val_acc: 0.7744
Epoch 13/200
45000/45000 [==============================] - 9s - loss: 0.5871 - acc: 0.7914 - val_loss: 0.6762 - val_acc: 0.7748
Epoch 14/200
45000/45000 [==============================] - 8s - loss: 0.5693 - acc: 0.8000 - val_loss: 0.6868 - val_acc: 0.7740
Epoch 15/200
45000/45000 [==============================] - 9s - loss: 0.5555 - acc: 0.8036 - val_loss: 0.6835 - val_acc: 0.7792
Epoch 16/200
45000/45000 [==============================] - 9s - loss: 0.5370 - acc: 0.8126 - val_loss: 0.6885 - val_acc: 0.7774
Epoch 17/200
45000/45000 [==============================] - 9s - loss: 0.5270 - acc: 0.8134 - val_loss: 0.6604 - val_acc: 0.7866
Epoch 18/200
45000/45000 [==============================] - 9s - loss: 0.5090 - acc: 0.8194 - val_loss: 0.6652 - val_acc: 0.7860
Epoch 19/200
45000/45000 [==============================] - 9s - loss: 0.5066 - acc: 0.8193 - val_loss: 0.6632 - val_acc: 0.7858
Epoch 20/200
45000/45000 [==============================] - 9s - loss: 0.4938 - acc: 0.8248 - val_loss: 0.6844 - val_acc: 0.7872
Epoch 21/200
45000/45000 [==============================] - 9s - loss: 0.4684 - acc: 0.8361 - val_loss: 0.6861 - val_acc: 0.7904
Epoch 22/200
45000/45000 [==============================] - 9s - loss: 0.4696 - acc: 0.8365 - val_loss: 0.6349 - val_acc: 0.7980
Epoch 23/200
45000/45000 [==============================] - 9s - loss: 0.4584 - acc: 0.8387 - val_loss: 0.6592 - val_acc: 0.7926
Epoch 24/200
45000/45000 [==============================] - 9s - loss: 0.4410 - acc: 0.8443 - val_loss: 0.6822 - val_acc: 0.7876
Epoch 25/200
45000/45000 [==============================] - 8s - loss: 0.4404 - acc: 0.8454 - val_loss: 0.7103 - val_acc: 0.7784
Epoch 26/200
45000/45000 [==============================] - 8s - loss: 0.4276 - acc: 0.8512 - val_loss: 0.6783 - val_acc: 0.7858
Epoch 27/200
45000/45000 [==============================] - 8s - loss: 0.4152 - acc: 0.8542 - val_loss: 0.6657 - val_acc: 0.7944
Epoch 28/200
45000/45000 [==============================] - 9s - loss: 0.4107 - acc: 0.8549 - val_loss: 0.6861 - val_acc: 0.7888
Epoch 29/200
45000/45000 [==============================] - 9s - loss: 0.4115 - acc: 0.8548 - val_loss: 0.6634 - val_acc: 0.7996
Epoch 30/200
45000/45000 [==============================] - 9s - loss: 0.4057 - acc: 0.8586 - val_loss: 0.7166 - val_acc: 0.7896
Epoch 31/200
45000/45000 [==============================] - 9s - loss: 0.3992 - acc: 0.8605 - val_loss: 0.6734 - val_acc: 0.7998
Epoch 32/200
45000/45000 [==============================] - 9s - loss: 0.3863 - acc: 0.8637 - val_loss: 0.7263 - val_acc: 0.7844
Epoch 33/200
45000/45000 [==============================] - 9s - loss: 0.3933 - acc: 0.8644 - val_loss: 0.6953 - val_acc: 0.7860
Epoch 34/200
45000/45000 [==============================] - 9s - loss: 0.3838 - acc: 0.8663 - val_loss: 0.7040 - val_acc: 0.7916
Epoch 35/200
45000/45000 [==============================] - 9s - loss: 0.3800 - acc: 0.8674 - val_loss: 0.7233 - val_acc: 0.7970
Epoch 36/200
45000/45000 [==============================] - 9s - loss: 0.3775 - acc: 0.8697 - val_loss: 0.7234 - val_acc: 0.7922
Epoch 37/200
45000/45000 [==============================] - 9s - loss: 0.3681 - acc: 0.8746 - val_loss: 0.6751 - val_acc: 0.7958
Epoch 38/200
45000/45000 [==============================] - 9s - loss: 0.3679 - acc: 0.8732 - val_loss: 0.7014 - val_acc: 0.7976
Epoch 39/200
45000/45000 [==============================] - 9s - loss: 0.3540 - acc: 0.8769 - val_loss: 0.6768 - val_acc: 0.8022
Epoch 40/200
45000/45000 [==============================] - 9s - loss: 0.3531 - acc: 0.8783 - val_loss: 0.7171 - val_acc: 0.7986
Epoch 41/200
45000/45000 [==============================] - 9s - loss: 0.3545 - acc: 0.8786 - val_loss: 0.7164 - val_acc: 0.7930
Epoch 42/200
45000/45000 [==============================] - 9s - loss: 0.3453 - acc: 0.8799 - val_loss: 0.7078 - val_acc: 0.7994
Epoch 43/200
45000/45000 [==============================] - 8s - loss: 0.3488 - acc: 0.8798 - val_loss: 0.7272 - val_acc: 0.7958
Epoch 44/200
45000/45000 [==============================] - 9s - loss: 0.3471 - acc: 0.8797 - val_loss: 0.7110 - val_acc: 0.7916
Epoch 45/200
45000/45000 [==============================] - 9s - loss: 0.3443 - acc: 0.8810 - val_loss: 0.7391 - val_acc: 0.7952
Epoch 46/200
45000/45000 [==============================] - 9s - loss: 0.3342 - acc: 0.8841 - val_loss: 0.7351 - val_acc: 0.7970
Epoch 47/200
45000/45000 [==============================] - 9s - loss: 0.3311 - acc: 0.8842 - val_loss: 0.7302 - val_acc: 0.8008
Epoch 48/200
45000/45000 [==============================] - 9s - loss: 0.3320 - acc: 0.8868 - val_loss: 0.7145 - val_acc: 0.8002
Epoch 49/200
45000/45000 [==============================] - 9s - loss: 0.3264 - acc: 0.8883 - val_loss: 0.7640 - val_acc: 0.7942
Epoch 50/200
45000/45000 [==============================] - 9s - loss: 0.3247 - acc: 0.8880 - val_loss: 0.7289 - val_acc: 0.7948
Epoch 51/200
45000/45000 [==============================] - 9s - loss: 0.3279 - acc: 0.8886 - val_loss: 0.7340 - val_acc: 0.7910
Epoch 52/200
45000/45000 [==============================] - 9s - loss: 0.3224 - acc: 0.8901 - val_loss: 0.7454 - val_acc: 0.7914
Epoch 53/200
45000/45000 [==============================] - 9s - loss: 0.3219 - acc: 0.8916 - val_loss: 0.7328 - val_acc: 0.8016
Epoch 54/200
45000/45000 [==============================] - 9s - loss: 0.3163 - acc: 0.8919 - val_loss: 0.7442 - val_acc: 0.7996
Epoch 55/200
45000/45000 [==============================] - 9s - loss: 0.3071 - acc: 0.8962 - val_loss: 0.7427 - val_acc: 0.7898
Epoch 56/200
45000/45000 [==============================] - 9s - loss: 0.3158 - acc: 0.8944 - val_loss: 0.7685 - val_acc: 0.7920
Epoch 57/200
45000/45000 [==============================] - 8s - loss: 0.3126 - acc: 0.8942 - val_loss: 0.7717 - val_acc: 0.8062
Epoch 58/200
45000/45000 [==============================] - 9s - loss: 0.3156 - acc: 0.8919 - val_loss: 0.6993 - val_acc: 0.7984
Epoch 59/200
45000/45000 [==============================] - 9s - loss: 0.3030 - acc: 0.8970 - val_loss: 0.7359 - val_acc: 0.8016
Epoch 60/200
45000/45000 [==============================] - 9s - loss: 0.3022 - acc: 0.8969 - val_loss: 0.7427 - val_acc: 0.7954
Epoch 61/200
45000/45000 [==============================] - 9s - loss: 0.3072 - acc: 0.8950 - val_loss: 0.7829 - val_acc: 0.7996
Epoch 62/200
45000/45000 [==============================] - 9s - loss: 0.2977 - acc: 0.8996 - val_loss: 0.8096 - val_acc: 0.7958
Epoch 63/200
45000/45000 [==============================] - 9s - loss: 0.3033 - acc: 0.8983 - val_loss: 0.7424 - val_acc: 0.7972
Epoch 64/200
45000/45000 [==============================] - 9s - loss: 0.2985 - acc: 0.9003 - val_loss: 0.7779 - val_acc: 0.7930
Epoch 65/200
45000/45000 [==============================] - 8s - loss: 0.2931 - acc: 0.9004 - val_loss: 0.7302 - val_acc: 0.8010
Epoch 66/200
45000/45000 [==============================] - 8s - loss: 0.2948 - acc: 0.8994 - val_loss: 0.7861 - val_acc: 0.7900
Epoch 67/200
45000/45000 [==============================] - 9s - loss: 0.2911 - acc: 0.9026 - val_loss: 0.7502 - val_acc: 0.7918
Epoch 68/200
45000/45000 [==============================] - 9s - loss: 0.2951 - acc: 0.9001 - val_loss: 0.7911 - val_acc: 0.7820
Epoch 69/200
45000/45000 [==============================] - 9s - loss: 0.2869 - acc: 0.9026 - val_loss: 0.8025 - val_acc: 0.8024
Epoch 70/200
45000/45000 [==============================] - 8s - loss: 0.2933 - acc: 0.9013 - val_loss: 0.7703 - val_acc: 0.7978
Epoch 71/200
45000/45000 [==============================] - 8s - loss: 0.2902 - acc: 0.9007 - val_loss: 0.7685 - val_acc: 0.7962
Epoch 72/200
45000/45000 [==============================] - 9s - loss: 0.2920 - acc: 0.9025 - val_loss: 0.7412 - val_acc: 0.7956
Epoch 73/200
45000/45000 [==============================] - 8s - loss: 0.2861 - acc: 0.9038 - val_loss: 0.7957 - val_acc: 0.8026
Epoch 74/200
45000/45000 [==============================] - 8s - loss: 0.2785 - acc: 0.9069 - val_loss: 0.7522 - val_acc: 0.8002
Epoch 75/200
45000/45000 [==============================] - 9s - loss: 0.2811 - acc: 0.9064 - val_loss: 0.8181 - val_acc: 0.7902
Epoch 76/200
45000/45000 [==============================] - 9s - loss: 0.2841 - acc: 0.9053 - val_loss: 0.7695 - val_acc: 0.7990
Epoch 77/200
45000/45000 [==============================] - 9s - loss: 0.2853 - acc: 0.9061 - val_loss: 0.7608 - val_acc: 0.7972
Epoch 78/200
45000/45000 [==============================] - 9s - loss: 0.2714 - acc: 0.9080 - val_loss: 0.7534 - val_acc: 0.8034
Epoch 79/200
45000/45000 [==============================] - 9s - loss: 0.2797 - acc: 0.9072 - val_loss: 0.7188 - val_acc: 0.7988
Epoch 80/200
45000/45000 [==============================] - 9s - loss: 0.2682 - acc: 0.9110 - val_loss: 0.7751 - val_acc: 0.7954
Epoch 81/200
45000/45000 [==============================] - 9s - loss: 0.2885 - acc: 0.9038 - val_loss: 0.7711 - val_acc: 0.8010
Epoch 82/200
45000/45000 [==============================] - 9s - loss: 0.2705 - acc: 0.9094 - val_loss: 0.7613 - val_acc: 0.8000
Epoch 83/200
45000/45000 [==============================] - 9s - loss: 0.2738 - acc: 0.9095 - val_loss: 0.8300 - val_acc: 0.7944
Epoch 84/200
45000/45000 [==============================] - 9s - loss: 0.2795 - acc: 0.9066 - val_loss: 0.8001 - val_acc: 0.7912
Epoch 85/200
45000/45000 [==============================] - 9s - loss: 0.2721 - acc: 0.9086 - val_loss: 0.7862 - val_acc: 0.8092
Epoch 86/200
45000/45000 [==============================] - 9s - loss: 0.2752 - acc: 0.9087 - val_loss: 0.7331 - val_acc: 0.7942
Epoch 87/200
45000/45000 [==============================] - 9s - loss: 0.2725 - acc: 0.9089 - val_loss: 0.7999 - val_acc: 0.7914
Epoch 88/200
45000/45000 [==============================] - 9s - loss: 0.2644 - acc: 0.9108 - val_loss: 0.7944 - val_acc: 0.7990
Epoch 89/200
45000/45000 [==============================] - 9s - loss: 0.2725 - acc: 0.9106 - val_loss: 0.7622 - val_acc: 0.8006
Epoch 90/200
45000/45000 [==============================] - 9s - loss: 0.2622 - acc: 0.9129 - val_loss: 0.8172 - val_acc: 0.7988
Epoch 91/200
45000/45000 [==============================] - 9s - loss: 0.2772 - acc: 0.9085 - val_loss: 0.8243 - val_acc: 0.8004
Epoch 92/200
45000/45000 [==============================] - 9s - loss: 0.2609 - acc: 0.9136 - val_loss: 0.7723 - val_acc: 0.7992
Epoch 93/200
45000/45000 [==============================] - 9s - loss: 0.2666 - acc: 0.9129 - val_loss: 0.8366 - val_acc: 0.7932
Epoch 94/200
45000/45000 [==============================] - 9s - loss: 0.2593 - acc: 0.9135 - val_loss: 0.8666 - val_acc: 0.7956
Epoch 95/200
45000/45000 [==============================] - 9s - loss: 0.2692 - acc: 0.9100 - val_loss: 0.8901 - val_acc: 0.7954
Epoch 96/200
45000/45000 [==============================] - 8s - loss: 0.2569 - acc: 0.9160 - val_loss: 0.8515 - val_acc: 0.8006
Epoch 97/200
45000/45000 [==============================] - 8s - loss: 0.2636 - acc: 0.9146 - val_loss: 0.8639 - val_acc: 0.7960
Epoch 98/200
45000/45000 [==============================] - 9s - loss: 0.2693 - acc: 0.9113 - val_loss: 0.7891 - val_acc: 0.7916
Epoch 99/200
45000/45000 [==============================] - 9s - loss: 0.2611 - acc: 0.9144 - val_loss: 0.8650 - val_acc: 0.7928
Epoch 100/200
45000/45000 [==============================] - 9s - loss: 0.2589 - acc: 0.9121 - val_loss: 0.8683 - val_acc: 0.7990
Epoch 101/200
45000/45000 [==============================] - 9s - loss: 0.2601 - acc: 0.9142 - val_loss: 0.9116 - val_acc: 0.8030
Epoch 102/200
45000/45000 [==============================] - 9s - loss: 0.2616 - acc: 0.9138 - val_loss: 0.8229 - val_acc: 0.7928
Epoch 103/200
45000/45000 [==============================] - 9s - loss: 0.2603 - acc: 0.9140 - val_loss: 0.8847 - val_acc: 0.7994
Epoch 104/200
45000/45000 [==============================] - 9s - loss: 0.2579 - acc: 0.9150 - val_loss: 0.9079 - val_acc: 0.8004
Epoch 105/200
45000/45000 [==============================] - 8s - loss: 0.2696 - acc: 0.9127 - val_loss: 0.7450 - val_acc: 0.8002
Epoch 106/200
45000/45000 [==============================] - 9s - loss: 0.2555 - acc: 0.9161 - val_loss: 0.8186 - val_acc: 0.7992
Epoch 107/200
45000/45000 [==============================] - 9s - loss: 0.2631 - acc: 0.9160 - val_loss: 0.8686 - val_acc: 0.7920
Epoch 108/200
45000/45000 [==============================] - 9s - loss: 0.2524 - acc: 0.9178 - val_loss: 0.9136 - val_acc: 0.7956
Epoch 109/200
45000/45000 [==============================] - 9s - loss: 0.2569 - acc: 0.9151 - val_loss: 0.8148 - val_acc: 0.7994
Epoch 110/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9150 - val_loss: 0.8826 - val_acc: 0.7984
Epoch 111/200
45000/45000 [==============================] - 9s - loss: 0.2520 - acc: 0.9155 - val_loss: 0.8621 - val_acc: 0.7980
Epoch 112/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9157 - val_loss: 0.8149 - val_acc: 0.8038
Epoch 113/200
45000/45000 [==============================] - 9s - loss: 0.2623 - acc: 0.9151 - val_loss: 0.8361 - val_acc: 0.7972
Epoch 114/200
45000/45000 [==============================] - 9s - loss: 0.2535 - acc: 0.9177 - val_loss: 0.8618 - val_acc: 0.7970
Epoch 115/200
45000/45000 [==============================] - 8s - loss: 0.2570 - acc: 0.9164 - val_loss: 0.7687 - val_acc: 0.8044
Epoch 116/200
45000/45000 [==============================] - 9s - loss: 0.2501 - acc: 0.9183 - val_loss: 0.8270 - val_acc: 0.7934
Epoch 117/200
45000/45000 [==============================] - 8s - loss: 0.2535 - acc: 0.9182 - val_loss: 0.7861 - val_acc: 0.7986
Epoch 118/200
45000/45000 [==============================] - 9s - loss: 0.2507 - acc: 0.9184 - val_loss: 0.8203 - val_acc: 0.7996
Epoch 119/200
45000/45000 [==============================] - 9s - loss: 0.2530 - acc: 0.9173 - val_loss: 0.8294 - val_acc: 0.7904
Epoch 120/200
45000/45000 [==============================] - 9s - loss: 0.2599 - acc: 0.9160 - val_loss: 0.8458 - val_acc: 0.7902
Epoch 121/200
45000/45000 [==============================] - 9s - loss: 0.2483 - acc: 0.9164 - val_loss: 0.7573 - val_acc: 0.7976
Epoch 122/200
45000/45000 [==============================] - 8s - loss: 0.2492 - acc: 0.9190 - val_loss: 0.8435 - val_acc: 0.8012
Epoch 123/200
45000/45000 [==============================] - 9s - loss: 0.2528 - acc: 0.9179 - val_loss: 0.8594 - val_acc: 0.7964
Epoch 124/200
45000/45000 [==============================] - 9s - loss: 0.2581 - acc: 0.9173 - val_loss: 0.9037 - val_acc: 0.7944
Epoch 125/200
45000/45000 [==============================] - 8s - loss: 0.2404 - acc: 0.9212 - val_loss: 0.7893 - val_acc: 0.7976
Epoch 126/200
45000/45000 [==============================] - 8s - loss: 0.2492 - acc: 0.9177 - val_loss: 0.8679 - val_acc: 0.7982
Epoch 127/200
45000/45000 [==============================] - 8s - loss: 0.2483 - acc: 0.9196 - val_loss: 0.8894 - val_acc: 0.7956
Epoch 128/200
45000/45000 [==============================] - 9s - loss: 0.2539 - acc: 0.9176 - val_loss: 0.8413 - val_acc: 0.8006
Epoch 129/200
45000/45000 [==============================] - 8s - loss: 0.2477 - acc: 0.9184 - val_loss: 0.8151 - val_acc: 0.7982
Epoch 130/200
45000/45000 [==============================] - 9s - loss: 0.2586 - acc: 0.9188 - val_loss: 0.8173 - val_acc: 0.7954
Epoch 131/200
45000/45000 [==============================] - 9s - loss: 0.2498 - acc: 0.9189 - val_loss: 0.8539 - val_acc: 0.7996
Epoch 132/200
45000/45000 [==============================] - 9s - loss: 0.2426 - acc: 0.9190 - val_loss: 0.8543 - val_acc: 0.7952
Epoch 133/200
45000/45000 [==============================] - 9s - loss: 0.2460 - acc: 0.9185 - val_loss: 0.8665 - val_acc: 0.8008
Epoch 134/200
45000/45000 [==============================] - 9s - loss: 0.2436 - acc: 0.9216 - val_loss: 0.8933 - val_acc: 0.7950
Epoch 135/200
45000/45000 [==============================] - 8s - loss: 0.2468 - acc: 0.9203 - val_loss: 0.8270 - val_acc: 0.7940
Epoch 136/200
45000/45000 [==============================] - 9s - loss: 0.2479 - acc: 0.9194 - val_loss: 0.8365 - val_acc: 0.8052
Epoch 137/200
45000/45000 [==============================] - 9s - loss: 0.2449 - acc: 0.9206 - val_loss: 0.7964 - val_acc: 0.8018
Epoch 138/200
45000/45000 [==============================] - 9s - loss: 0.2440 - acc: 0.9220 - val_loss: 0.8784 - val_acc: 0.7914
Epoch 139/200
45000/45000 [==============================] - 9s - loss: 0.2485 - acc: 0.9198 - val_loss: 0.8259 - val_acc: 0.7852
Epoch 140/200
45000/45000 [==============================] - 9s - loss: 0.2482 - acc: 0.9204 - val_loss: 0.8954 - val_acc: 0.7960
Epoch 141/200
45000/45000 [==============================] - 9s - loss: 0.2344 - acc: 0.9249 - val_loss: 0.8708 - val_acc: 0.7874
Epoch 142/200
45000/45000 [==============================] - 9s - loss: 0.2476 - acc: 0.9204 - val_loss: 0.9190 - val_acc: 0.7954
Epoch 143/200
45000/45000 [==============================] - 9s - loss: 0.2415 - acc: 0.9223 - val_loss: 0.9607 - val_acc: 0.7960
Epoch 144/200
45000/45000 [==============================] - 9s - loss: 0.2377 - acc: 0.9232 - val_loss: 0.8987 - val_acc: 0.7970
Epoch 145/200
45000/45000 [==============================] - 9s - loss: 0.2481 - acc: 0.9201 - val_loss: 0.8611 - val_acc: 0.8048
Epoch 146/200
45000/45000 [==============================] - 9s - loss: 0.2504 - acc: 0.9197 - val_loss: 0.8411 - val_acc: 0.7938
Epoch 147/200
45000/45000 [==============================] - 9s - loss: 0.2450 - acc: 0.9216 - val_loss: 0.7839 - val_acc: 0.8028
Epoch 148/200
45000/45000 [==============================] - 9s - loss: 0.2327 - acc: 0.9250 - val_loss: 0.8910 - val_acc: 0.8054
Epoch 149/200
45000/45000 [==============================] - 9s - loss: 0.2432 - acc: 0.9219 - val_loss: 0.8568 - val_acc: 0.8000
Epoch 150/200
45000/45000 [==============================] - 9s - loss: 0.2436 - acc: 0.9236 - val_loss: 0.9061 - val_acc: 0.7938
Epoch 151/200
45000/45000 [==============================] - 9s - loss: 0.2434 - acc: 0.9222 - val_loss: 0.8439 - val_acc: 0.7986
Epoch 152/200
45000/45000 [==============================] - 9s - loss: 0.2439 - acc: 0.9225 - val_loss: 0.9002 - val_acc: 0.7994
Epoch 153/200
45000/45000 [==============================] - 8s - loss: 0.2373 - acc: 0.9237 - val_loss: 0.8756 - val_acc: 0.7880
Epoch 154/200
45000/45000 [==============================] - 8s - loss: 0.2359 - acc: 0.9238 - val_loss: 0.8514 - val_acc: 0.7936
Epoch 155/200
45000/45000 [==============================] - 9s - loss: 0.2435 - acc: 0.9222 - val_loss: 0.8377 - val_acc: 0.8080
Epoch 156/200
45000/45000 [==============================] - 9s - loss: 0.2478 - acc: 0.9204 - val_loss: 0.8831 - val_acc: 0.7992
Epoch 157/200
45000/45000 [==============================] - 9s - loss: 0.2337 - acc: 0.9253 - val_loss: 0.8453 - val_acc: 0.7994
Epoch 158/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9257 - val_loss: 0.9027 - val_acc: 0.7882
Epoch 159/200
45000/45000 [==============================] - 9s - loss: 0.2384 - acc: 0.9230 - val_loss: 0.9121 - val_acc: 0.8016
Epoch 160/200
45000/45000 [==============================] - 9s - loss: 0.2481 - acc: 0.9217 - val_loss: 0.9495 - val_acc: 0.7974
Epoch 161/200
45000/45000 [==============================] - 9s - loss: 0.2450 - acc: 0.9224 - val_loss: 0.8510 - val_acc: 0.7884
Epoch 162/200
45000/45000 [==============================] - 9s - loss: 0.2433 - acc: 0.9220 - val_loss: 0.8979 - val_acc: 0.7948
Epoch 163/200
45000/45000 [==============================] - 9s - loss: 0.2339 - acc: 0.9262 - val_loss: 0.8979 - val_acc: 0.7978
Epoch 164/200
45000/45000 [==============================] - 9s - loss: 0.2298 - acc: 0.9257 - val_loss: 0.9036 - val_acc: 0.7990
Epoch 165/200
45000/45000 [==============================] - 9s - loss: 0.2404 - acc: 0.9236 - val_loss: 0.8341 - val_acc: 0.8052
Epoch 166/200
45000/45000 [==============================] - 9s - loss: 0.2402 - acc: 0.9227 - val_loss: 0.8731 - val_acc: 0.7996
Epoch 167/200
45000/45000 [==============================] - 9s - loss: 0.2367 - acc: 0.9250 - val_loss: 0.9218 - val_acc: 0.7992
Epoch 168/200
45000/45000 [==============================] - 9s - loss: 0.2267 - acc: 0.9262 - val_loss: 0.8767 - val_acc: 0.7922
Epoch 169/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9254 - val_loss: 0.8418 - val_acc: 0.8038
Epoch 170/200
45000/45000 [==============================] - 9s - loss: 0.2434 - acc: 0.9232 - val_loss: 0.8362 - val_acc: 0.7920
Epoch 171/200
45000/45000 [==============================] - 9s - loss: 0.2328 - acc: 0.9265 - val_loss: 0.8712 - val_acc: 0.7950
Epoch 172/200
45000/45000 [==============================] - 9s - loss: 0.2346 - acc: 0.9262 - val_loss: 0.9256 - val_acc: 0.7976
Epoch 173/200
45000/45000 [==============================] - 8s - loss: 0.2382 - acc: 0.9242 - val_loss: 0.8875 - val_acc: 0.7982
Epoch 174/200
45000/45000 [==============================] - 9s - loss: 0.2400 - acc: 0.9239 - val_loss: 0.8264 - val_acc: 0.7864
Epoch 175/200
45000/45000 [==============================] - 9s - loss: 0.2334 - acc: 0.9261 - val_loss: 0.9178 - val_acc: 0.8014
Epoch 176/200
45000/45000 [==============================] - 9s - loss: 0.2427 - acc: 0.9219 - val_loss: 0.8458 - val_acc: 0.7920
Epoch 177/200
45000/45000 [==============================] - 9s - loss: 0.2310 - acc: 0.9257 - val_loss: 0.9171 - val_acc: 0.8062
Epoch 178/200
45000/45000 [==============================] - 9s - loss: 0.2310 - acc: 0.9265 - val_loss: 0.8544 - val_acc: 0.7990
Epoch 179/200
45000/45000 [==============================] - 9s - loss: 0.2378 - acc: 0.9240 - val_loss: 0.9259 - val_acc: 0.8000
Epoch 180/200
45000/45000 [==============================] - 9s - loss: 0.2381 - acc: 0.9242 - val_loss: 0.8573 - val_acc: 0.8056
Epoch 181/200
45000/45000 [==============================] - 9s - loss: 0.2231 - acc: 0.9297 - val_loss: 0.8935 - val_acc: 0.8002
Epoch 182/200
45000/45000 [==============================] - 9s - loss: 0.2419 - acc: 0.9248 - val_loss: 1.0145 - val_acc: 0.7900
Epoch 183/200
45000/45000 [==============================] - 9s - loss: 0.2336 - acc: 0.9266 - val_loss: 0.8838 - val_acc: 0.8006
Epoch 184/200
45000/45000 [==============================] - 9s - loss: 0.2429 - acc: 0.9242 - val_loss: 0.8685 - val_acc: 0.7918
Epoch 185/200
45000/45000 [==============================] - 9s - loss: 0.2317 - acc: 0.9260 - val_loss: 0.8297 - val_acc: 0.7942
Epoch 186/200
45000/45000 [==============================] - 9s - loss: 0.2330 - acc: 0.9264 - val_loss: 0.8831 - val_acc: 0.8026
Epoch 187/200
45000/45000 [==============================] - 9s - loss: 0.2353 - acc: 0.9254 - val_loss: 0.8934 - val_acc: 0.7956
Epoch 188/200
45000/45000 [==============================] - 9s - loss: 0.2312 - acc: 0.9247 - val_loss: 0.9275 - val_acc: 0.8042
Epoch 189/200
45000/45000 [==============================] - 9s - loss: 0.2239 - acc: 0.9282 - val_loss: 0.9246 - val_acc: 0.7934
Epoch 190/200
45000/45000 [==============================] - 9s - loss: 0.2349 - acc: 0.9253 - val_loss: 0.8628 - val_acc: 0.8000
Epoch 191/200
45000/45000 [==============================] - 9s - loss: 0.2313 - acc: 0.9266 - val_loss: 0.9020 - val_acc: 0.7978
Epoch 192/200
45000/45000 [==============================] - 9s - loss: 0.2358 - acc: 0.9254 - val_loss: 0.9481 - val_acc: 0.7966
Epoch 193/200
45000/45000 [==============================] - 9s - loss: 0.2298 - acc: 0.9276 - val_loss: 0.8791 - val_acc: 0.8010
Epoch 194/200
45000/45000 [==============================] - 9s - loss: 0.2279 - acc: 0.9265 - val_loss: 0.8890 - val_acc: 0.7976
Epoch 195/200
45000/45000 [==============================] - 9s - loss: 0.2330 - acc: 0.9273 - val_loss: 0.8893 - val_acc: 0.7890
Epoch 196/200
45000/45000 [==============================] - 9s - loss: 0.2416 - acc: 0.9243 - val_loss: 0.9002 - val_acc: 0.7922
Epoch 197/200
45000/45000 [==============================] - 9s - loss: 0.2309 - acc: 0.9273 - val_loss: 0.9232 - val_acc: 0.7990
Epoch 198/200
45000/45000 [==============================] - 9s - loss: 0.2247 - acc: 0.9278 - val_loss: 0.9474 - val_acc: 0.7980
Epoch 199/200
45000/45000 [==============================] - 9s - loss: 0.2335 - acc: 0.9256 - val_loss: 0.9177 - val_acc: 0.8000
Epoch 200/200
45000/45000 [==============================] - 9s - loss: 0.2378 - acc: 0.9254 - val_loss: 0.9205 - val_acc: 0.7966
9984/10000 [============================>.] - ETA: 0s
[0.97292723369598388, 0.7853]
Наша модель достигает точности около 76.6% на тестовом множестве; для такой сложной задачи, где даже человеческий взгляд показывает точность всего около 90%, а также учитывая относительную простоту модели, это вполне достойный результат. Тем не менее, более сложные модели в последних исследованиях достигали точности 96.53%.
Полагаю, что тонкая настройка модели, если в вашем распоряжении нет графического процессора, будет крайне затруднительна. Тем не менее, советую вам попробовать применить эту модель к набору MNIST с прошлого урока; на CNN с dropout’ом у вас почти без усилий должно получиться достигнуть точности 99.3%.
Заключение
Сегодня мы изучили базовые понятия сверточных нейронных сетей, рассмотрели проблему переобучения и выяснили в общих чертах, как ее решают с помощью регуляризации (в частности, методом dropout), а также успешно построили четырехслойную глубокую CNN в Keras, протестировав ее на CIFAR-10 и уложившись в 50 строк кода.
В следующий раз мы рассмотрим сразу несколько тем, изучим приемы и хитрости, связанные с тонкой настройкой моделей, достижения максимальной производительности и контролем за переобучением.
Автор: Wunder Fund