Всем доброго времени суток. В прошлых статьях мы сравнивали два эвристических алгоритма оптимизации на симметричной задаче коммивояжера таких как: ACS (ant colony system — муравьиный алгоритм) и SA (simulating annealing — алгоритм имитации отжига). Как мы убедились у каждого свои плюсы и минусы.
Плюсы SA — относительно высокая скорость алгоритма, простота реализации. Из минусов — алгоритм не является «гибким», также нет так называемой «способности к перестроению фигуры». Тем кто хочет вникнуть в суть алгоритма имитационного отжига отсылаю к данной статье.
Плюсы AS(ACS) — присутствие коллективизма, сходимость алгоритма от итерации к итерации, способность к перестроению фигуры (всегда ищет альтернативные пути, по сути, при правильном подборе параметров не застревает на локальном оптимуме), возможность частичного параллелизма. Из минусов — долгое время алгоритма, сложность при высоком количестве вершин. Тем кто хочет вникнуть в суть муравьиного алгоритма отсылаю к сайту. Также можете посмотреть код, написанный на MatLab в моих предыдущих статьях, там в комментариях можно понять принцип.
Сегодня я хотел бы показать Вам первую версию алгоритма, который вобрал в себя лучшее из разных алгоритмов, и который способен найти с с первой попытки с высокой вероятностью глобальный оптимальный путь до 100 вершин менее чем за 5 секунд на обычном домашнем ПК. Показывать все буду стараться на примерах с графическими иллюстрациями. Код написан на MatLab. Местами в его стихии — векторно, если у кого-нибудь возникнут проблемы при переноса алгоритма на свой язык — пишите в комментариях. Тем кто заинтересовался более серьезно, либо те кто хочет реализовать свою версию — предлагаю посмотреть предыдущие статьи, а также посмотреть полный код алгоритма, который будет приложен снизу статьи. В комментариях старался расписать каждую строчку.
Сразу отмечу, что возможно данный алгоритм уже существует, но я не нашел его в просторах глобальной сети. Итак каким он должен быть в реализации данной статьи:
1 — Максимально простым
2 — Максимально быстрым
3 — Возможность распараллеливания на CPU (в том числе модных на сегодня GPU)
4 — Гибким (возможность модернизирования, изменчивость параметров)
5 — Менее зависим от случайных параметров
6 — Возможность перестроения фигуры
Под чем я подразумеваю перестроение фигуры см. ниже.
Перестроение фигуры TSP на задаче Eil101 (traveling salesman problem):
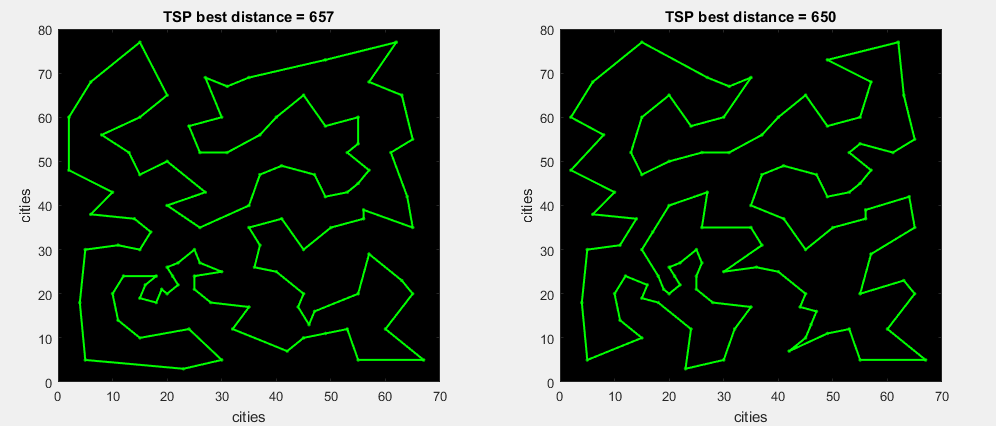
На изображении видно что дистанция обоих маршрутов отличается на 1%, однако у них совсем разные маршруты. То есть совсем разные фигуры. Хороший алгоритм должен создавать как можно больше подобных фигур. У SA это слабо развито.
Метод имитации отжига (как мы убедились в предыдущих статьях) при начальной высокой температуре, а также при медленно падающей температуре — способен достичь хороших результатов, однако это значительно увеличивает время алгоритма, также как и совсем не гарантирует нахождения глобального лучшего пути. Другое дело, если мы разом запустим несколько алгоритмов SA, занесем в массив результаты каждого и выберем лучший.
Один из минусов классического алгоритма SA это то, что в нем слишком много «random-а», сначала случайно выбираем две вершины, потом снова «random», чтобы принять или не принять худшее решение. В данном алгоритме я старался максимально снизить долю случайности.
Поэтому в данном алгоритме мы, вместо того чтобы «рандомить» две вершины, сразу переберем все возможные части инвертации пути. Напомню, что наша цель только глобальный оптимум, только хардкор. Точнее не глобальный, а лучший найденный на сегодняшний день.
Уточнение:
Есть маршрут: [1,2,3,4,5,6,7,8] — путешественник посещает сначала 1-ый город, потом 2-ой и т.д. «Рандомить две вершины» означает случайно выбрать два числа (равномерным распределением), скажем пусть будут 2 и 6, затем инвертировать путь между ними. Путь примет вид: [1,6,5,4,3,2,8].
Полный перебор частей инвертации пути выносим в функцию, которая принимает на вход маршрут (любой, даже самый некорректный), ищет наиболее выгодную часть маршрута для разворота, разворачивает его, дальше снова ищет наиболее выгодную часть маршрута с учетом предыдущих изменений и повторяет цикл до тех пор, пока ни одна замена части маршрута не улучшит дистанцию.
Данный метод известен как алгоритм 2opt. Однако в классическом 2opt алгоритме мы сразу разворачиваем часть маршрута, которое улучшает результат, здесь же мы ищем помимо стандартного 2opt еще и «лучшую замену».
Графическая иллюстрация:
на 1-ой gif анимации алгоритм сразу разворачивает найденную часть маршрута, которая улучшает общую дистанцию (стандартный 2-opt)
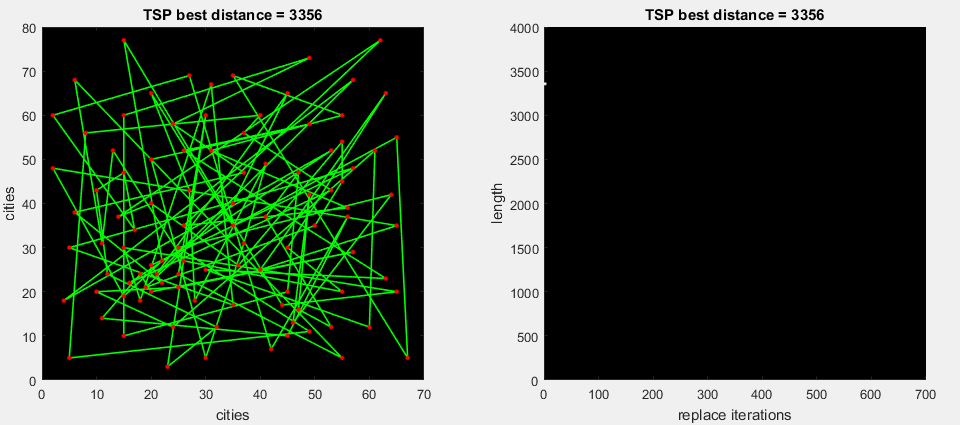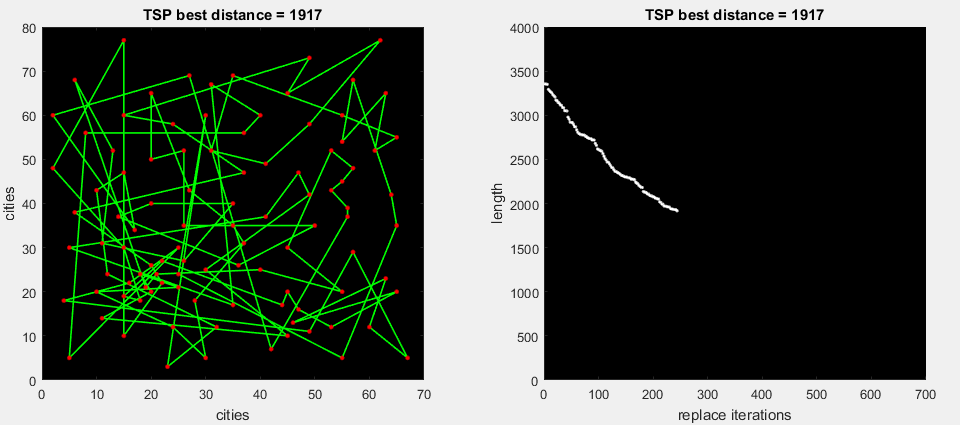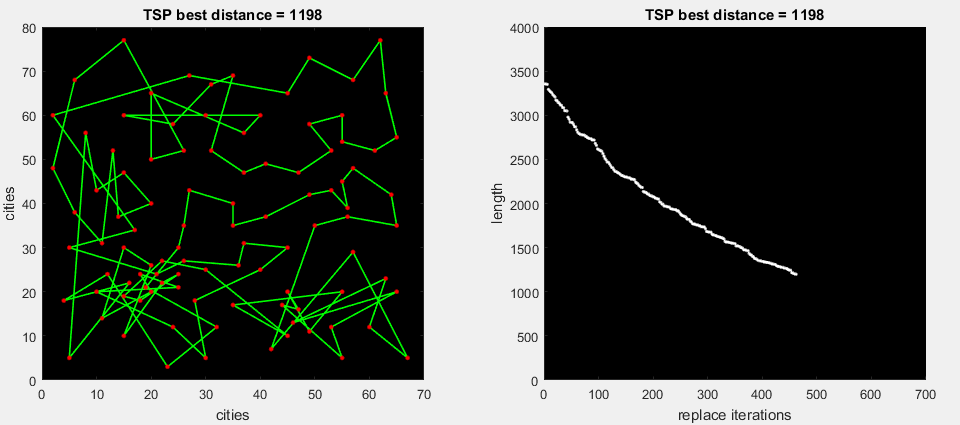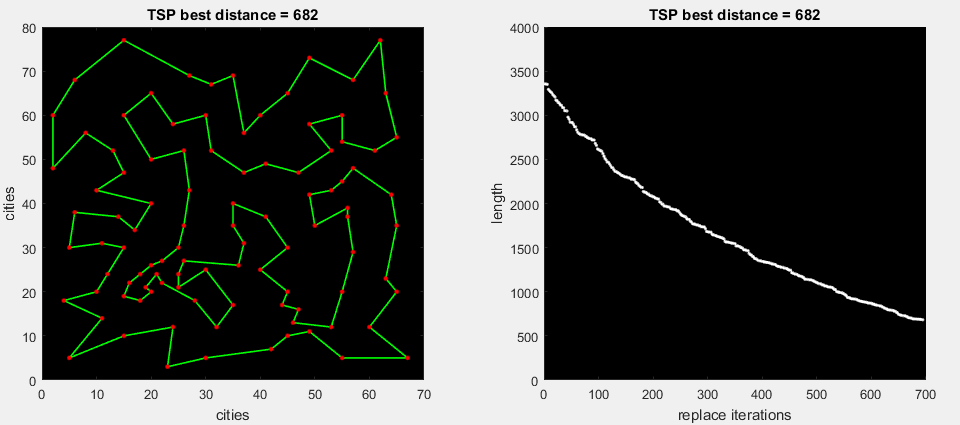
на 2-ой gif анимации алгоритм прогоняет все возможные замены части маршрута, далее разворачивает наиболее максимальную дельту (m. 2-opt)
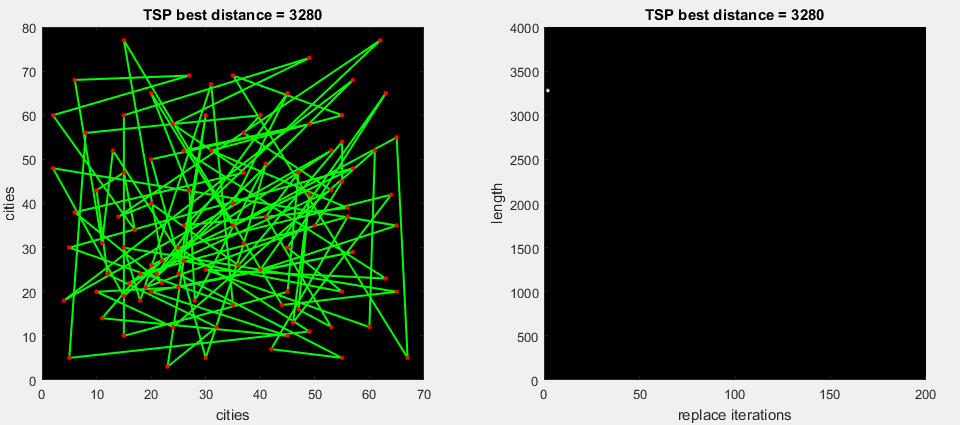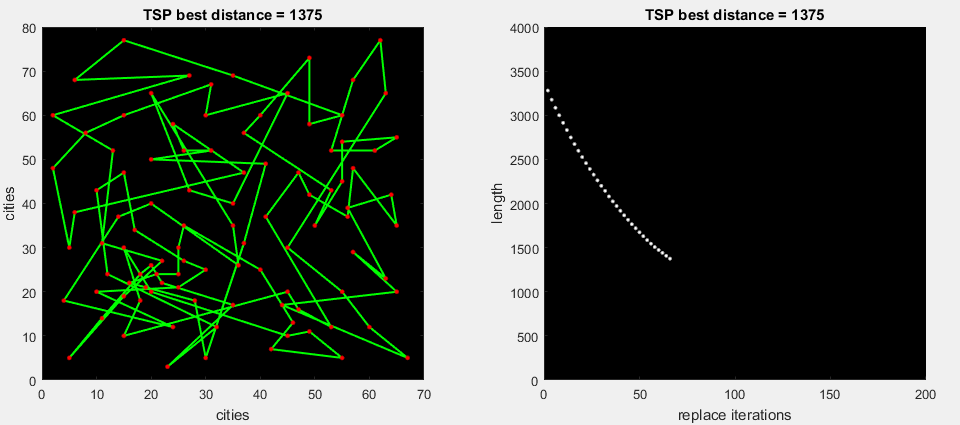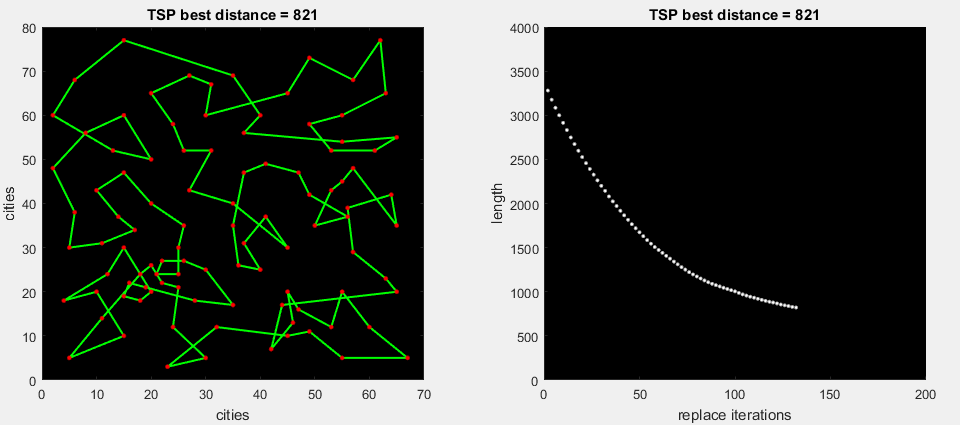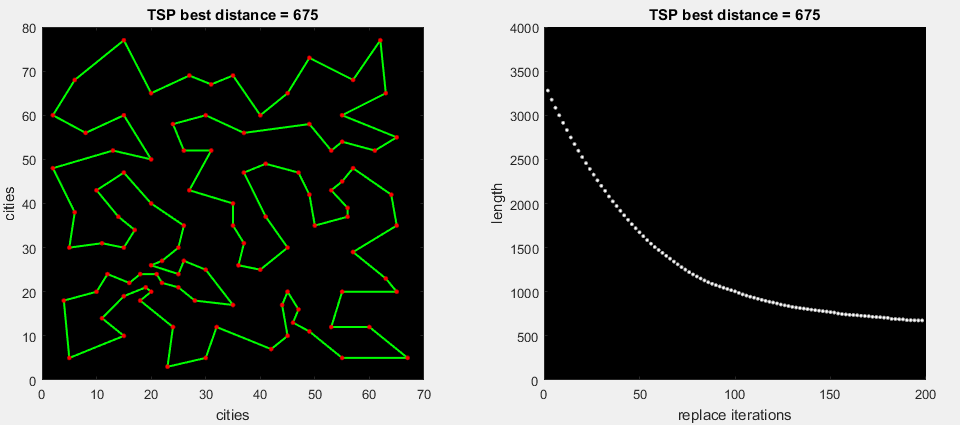
В сегодняшнем алгоритме будем использовать второй вариант, поскольку по серии тестов он показывает куда лучшие результаты. Первый вариант оставим на доработку.
Итак у нас есть две функции которые оптимизируют маршрут неким «модернизированным методом имитации отжига». Осталось только передать параллельным циклом (в MatLabe оператор parfor позволяет задействовать все ядра ПК) в функцию пару тысяч таких маршрутов (которые тоже будут созданы параллельным циклом) и выбрать лучший из них.
% Функция перебора всех пар ребер для задачи коммивояжера
% модернизированная версия метода отжига (лучшая замена)
% dist - матрица дистанций
% route - маршрут
% openclose - считать как закрытую или открытую задачу
%------------------------------------------------------------------------
function [tour, distance] = all_brute_best(dist,route,n)
global_diff = -0.1;
best_dist = inf;
% если перестановки ребер не улучшают результат, выходим из цикла
while global_diff < 0
global_diff = 0;
p1 = route(n);
% Цикл по всем ребрам
for i = 1:n-2
t1 = p1;
p1 = route(i);
t2 = route(i+1);
spd_var = dist(t1,p1);
for j = i+2:n
p2 = t2;
t2 = route(j);
diff = (dist(t1,p2) - dist(p2,t2))...
+ (dist(p1,t2) - spd_var);
% индексы на инвертацию пути с наибольшим эффектом
if global_diff > diff
global_diff = diff;
% "лучшие" индексы для замены ребер
imin = i; jmin = j;
end
end
end
% Инвертируем путь
if global_diff < 0
route(imin:jmin-1) = route(jmin-1:-1:imin);
end
end
%--------------------------------------------------------------------
% считаем общее расстояние
cur_dist = 0;
for i = 1:n-1
cur_dist = cur_dist + dist(route(i),route(i+1));
end
% считаем возврат в первый город
cur_dist = cur_dist + dist(route(1),route(end));
%--------------------------------------------------------------------
% выбираем лучший маршрут
if cur_dist < best_dist
best_route = route;
best_dist = cur_dist;
end
% переборный маршрут - его дистанция
distance = best_dist;
% сам маршрут
tour = best_route;
end
% Функция перебора всех пар ребер для задачи коммивояжера
% модернизированная версия метода отжига (каждая замена)
% dist - матрица дистанций
% route - маршрут
% openclose - считать как закрытую или открытую задачу
%-------------------------------------------------------------------------
function [tour, distance] = all_brute_first(dist,route,n)
global_diff = -0.1;
best_dist = inf;
% если перестановки ребер не улучшают результат, выходим из цикла
while global_diff < 0
global_diff = 0;
p1 = route(n);
% Цикл по всем ребрам
for i = 1:n-2
t1 = p1;
p1 = route(i);
t2 = route(i+1);
spd_var = dist(t1,p1);
for j = i+2:n
p2 = t2;
t2 = route(j);
diff = (dist(t1,p2) - dist(p2,t2))...
+ (dist(p1,t2) - spd_var);
% индексы на инвертацию пути с наибольшим эффектом
if diff < 0
global_diff = diff;
% "лучшие" индексы для замены ребер
imin = i; jmin = j;
break
end
end
% выход с цикла
if diff < 0
break
end
end
% Инвертируем путь
if global_diff < 0
route(imin:jmin-1) = route(jmin-1:-1:imin);
end
end
%--------------------------------------------------------------------
% считаем общее расстояние
cur_dist = 0;
for i = 1:n-1
cur_dist = cur_dist + dist(route(i),route(i+1));
end
% считаем возврат в первый город
cur_dist = cur_dist + dist(route(1),route(end));
%--------------------------------------------------------------------
% выбираем лучший маршрут
if cur_dist < best_dist
best_route = route;
best_dist = cur_dist;
end
% переборный маршрут - его дистанция
distance = best_dist;
% сам маршрут
tour = best_route;
end
Вот тут и начинается самое интересное.
Какие маршруты передавать? Естественно при выходе они должны максимально содержать разные фигуры (см. выше). Также если передавать просто рандомный массив, то глобально лучшего результата мы и не увидим. Итак пусть наш массив маршрутов на вход функции «all_brute_best» будет состоять из разных алгоритмов.
Первое, пришедшее сразу на ум это метод ближайшего соседа. Выйдем с каждого города по разу, и получим массив размерностью nxn маршрутов (n — количество городов). Затем данный массив передадим в функцию оптимизации.
На Matlabe ближайший город будет посещаться следующим образом:
parfor k = 1:n
% временная матрица (выгорает при посещении вершины)
dist_temp = dist;
% маршрут по ближайшим городам
route = zeros(1,n);
% первая стартовая позиция
next_point = start_route(k);
% заполнение маршрута
route(1) = next_point;
% посещаем каждый ближайший город
for e = 2:n
% выгорание матрицы
dist_temp(next_point,:) = nan;
% поиск ближайшего оставшегося города
[~,next_point] = min(dist_temp(:,next_point));
% заполнение маршрута
route(e) = next_point;
end
% првоеряем на уникальность и перестраиваем маршруты с 1-ого города
if check_routes == true
route = check_tour(route);
end
% массив машрутов
arr_route_in(k,:) = route;
end
Вообще, задачи TSP (traveling salesman problem) решались многими. Решались они и самыми «навароченными» алгоритмами. Так на сайте выкладываются лучшие найденные решения на сегодняшний день.
Проверим алгоритм на задаче Eil76, наглядная работа которого представлена ниже. Лучший найденный путь составляет 538.
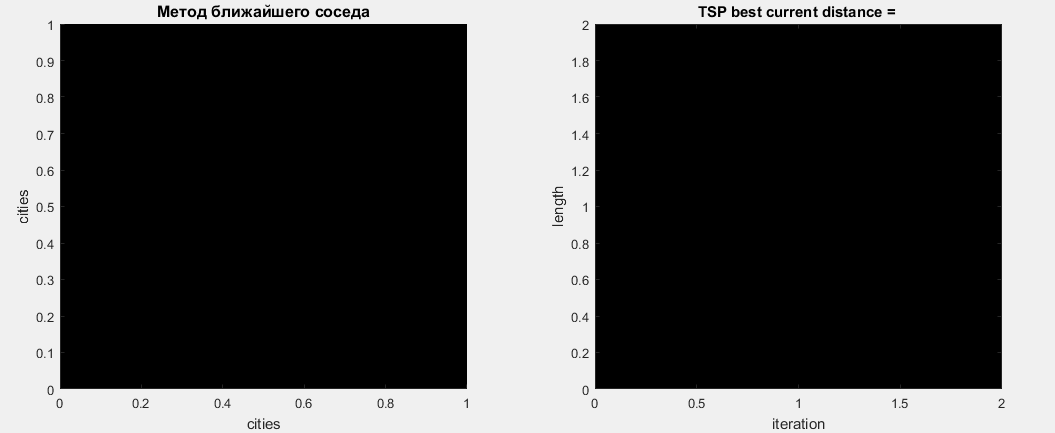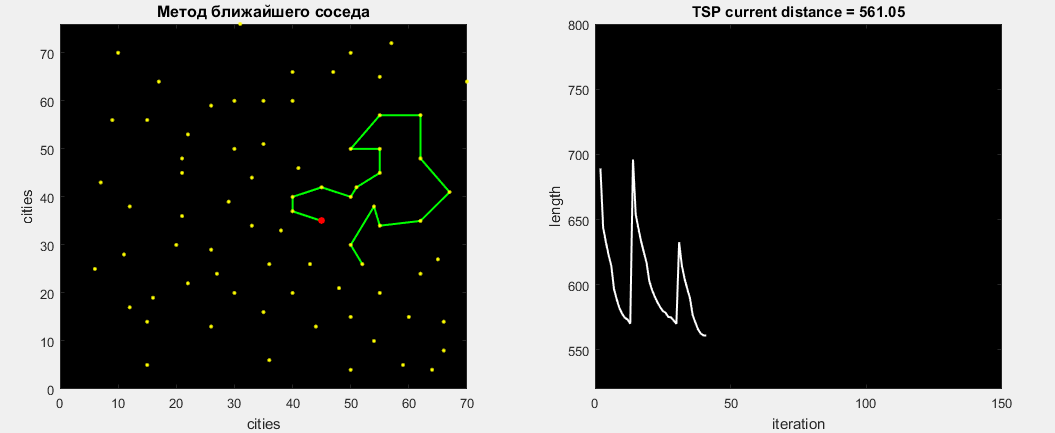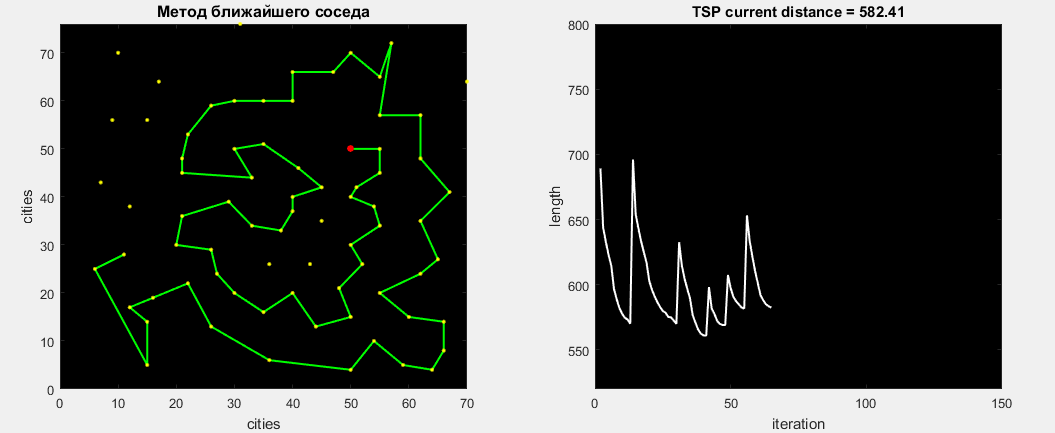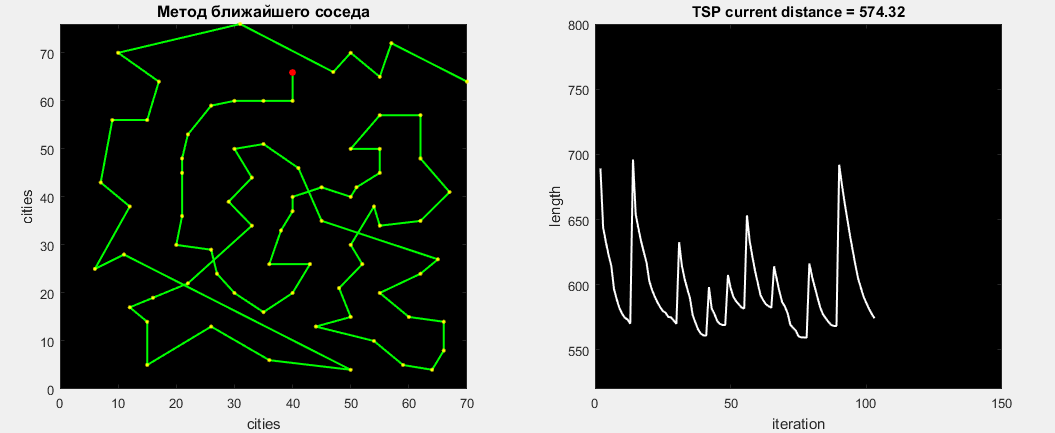
После совершения всех 76 оптимизаций получаем лучший найденный маршрут — 545. Затраченное время 0,15 секунды. Данный алгоритм всегда будет находить расстояние в 545, так как доли случайности в нем нет. Ошибка от глобального составляет 1.3%.
Теперь самое интересное. Как Вы наверно заметили мы только смешали жадный алгоритм, метод brute force (полный перебор) и имитационный отжиг. Теперь пришло время добавить немного муравьиного алгоритма. Сейчас в нашем алгоритме до передачи в функцию оптимизации с вероятностью 100% осуществляется переход в ближайший город. Наша задача, дабы отыскать лучший найденный маршрут, составить как можно больше «фигур» и передать их в функцию. Как мы помним у муравьиного алгоритма (AS) вероятность перехода из вершины i в вершину j определяется по следующей формуле:
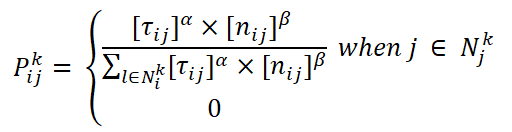
где [τ(i,j)] — уровень феромона на ребре (i,j), [n(i,j)] — вес обратный расстоянию на ребре (i,j), β — регулируемый параметр, чем он выше, тем алгоритм будет склонен выбирать ребро, имеющее меньшее расстояние. Поскольку в данном алгоритме феромонов, нет, то уберем их. Оставим только уровень «жадности» алгоритма. Ведем как в ACS вероятность выбора не посещенной вершины. Либо выбираем только кратчайший город, либо переходим следующим образом:
Вероятность выбора следующего ребра будет обратно пропорциональна его длине. Также введем переменную, отвечающую за выборку еще не посещенных городов. То есть при выборе очередной вершины мы не будем учитывать все оставшиеся, а будем выбирать среди N-ого количества оставшихся вершин. N — параметр задаваемый пользователем. Данную идею взял у генетического алгоритма. В генетическом алгоритме есть понятие «отбора», на этапе котором нужно из всей текущей популяции выбрать определенную долю, которая останется «жить». Вероятность выживания особи должна зависеть от значения функции приспособленности. Здесь же значение функции приспособленности — расстояние ребра, а популяция — доля оставшихся не посещенных городов. Просто из всей популяции мы выбираем только одну «особь», т.е. одну вершину. Формула вероятности принятия следующего ребра примет вид:
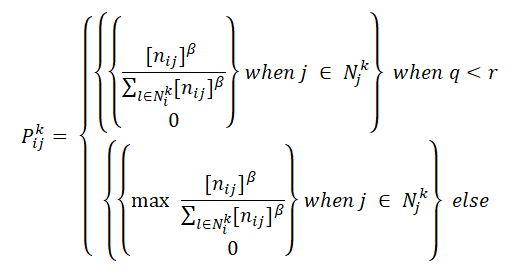
где q — вероятность принятие альтернативного решения (не обязательно кратчайшего ребра)
r — случайное число [0;1]
N — ребра, участвующие в выборе (сортируемые)
Таким образом мы сформируем множество «контролируемых» различных маршрутов на вход функции all_brute. Под словом контролируемых подразумевается контроль случайности маршрута. Чем более параметр q будет стремиться к 1, так же как и N будет стремиться к общему количеству городов, тем более случайным будет поиск.
% (probability several route)
% Функция, возвращаемая массив маршрутов методом рулетки среди топ вершин
% dist - матрица расстояний
% tour_sev - кол-во создаваемых маршрутов
% n - кол-во вершин
% tour_select - кол-во потенциальных вершин
% check_routes - проверка на уникальность и перестроение вершин
% p_change - вероятность перехода на альтернативный путь
%-------------------------------------------------------------------------
function [arr_several_route] = psr(dist,tour_sev,n,tour_select,cr,p_change)
% возвращаемый массив (память)
arr_several_route = zeros(tour_sev,n);
parfor k = 1:tour_sev
% временная матрица (выгорает при посещении вершины)
dist_temp = dist;
% маршрут по ближайшим городам
route = zeros(1,n);
% первая стартовая позиция (в данном случае случайная)
next_point = randi([1,n]);
% заполнение первой вершины маршрута
route(1) = next_point;
% счетчик
count_var = 0;
% цикл по посещениям вершин
for e = 2:n
% выгорание матрицы посещенной вершины
dist_temp(next_point,:) = nan;
% счетчик
count_var = count_var + 1;
% вероятность выбора альтернативной вершины
if rand(1) > p_change
% выбираем безусловно кратчайший путь к k-ому городу
% поиск ближайшего оставшегося города
[~,next_point] = min(dist_temp(:,next_point));
else
% выбираем альтернативную вершину
% массив дистанций перехода к следующей вершине (обратные)
arr_next = 1./(dist_temp(:,next_point));
% сайт хабрахабр транспонирование матрицы в массиве не
% воспринимает, поэтому переменная "habrahabr_vis" лишняя
habrahabr_vis = (1:1:n)';
% приписываем индексы к массиву
arr_next = [arr_next, habrahabr_vis];
% сортируем массив вместе с индексами
arr_next_sort = sortrows(arr_next,1);
% чтобы диапозон rand был корректен
if (n - count_var) < tour_select
tour_select_fun = (n - count_var);
else
tour_select_fun = tour_select;
end
% считаем вероятность перехода среди топ вершин
P = arr_next_sort(1:tour_select_fun,:);
P(:,1) = P(:,1)./sum(P(:,1));
randNumb = rand;
next_point = P(find(cumsum(P) >= randNumb, 1, 'first'),2);
end
% заполнение маршрута
route(e) = next_point;
end
% првоеряем и перестраиваем маршруты с 1-ого города
if cr == true
route = check_tour(route);
end
% заполнение массива маршрутов (возвращаемый результат)
arr_several_route(k,:) = route;
end
Итак, смотрим результаты на различных задачах:
Точные решения:
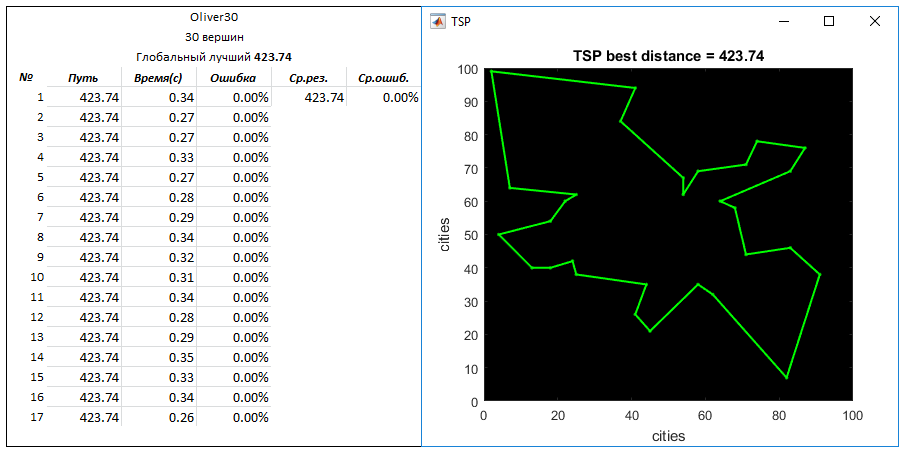
Задача Oliver30 (30 вершин). Глобальный лучший путь — 423.741
Параметры: кол-во создаваемых маршрутов на вход — 500
q = 0.03
N = 10
Задача Eil51 (51 вершина). Глобальный лучший путь — 426
Параметры: кол-во создаваемых маршрутов на вход — 2500
q = 0.03
N = 5
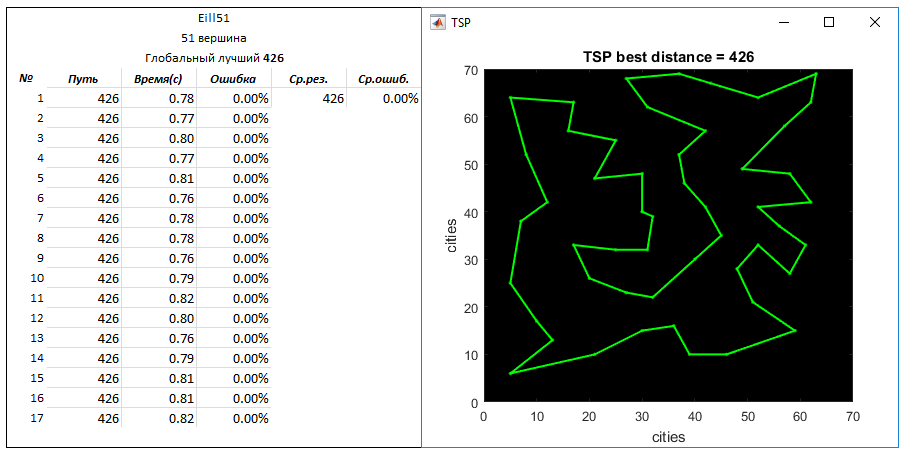
Задача Eil76 (76 вершин). Глобальный лучший путь — 538
Параметры: кол-во создаваемых маршрутов на вход — 4000
q = 0.03
N = 10
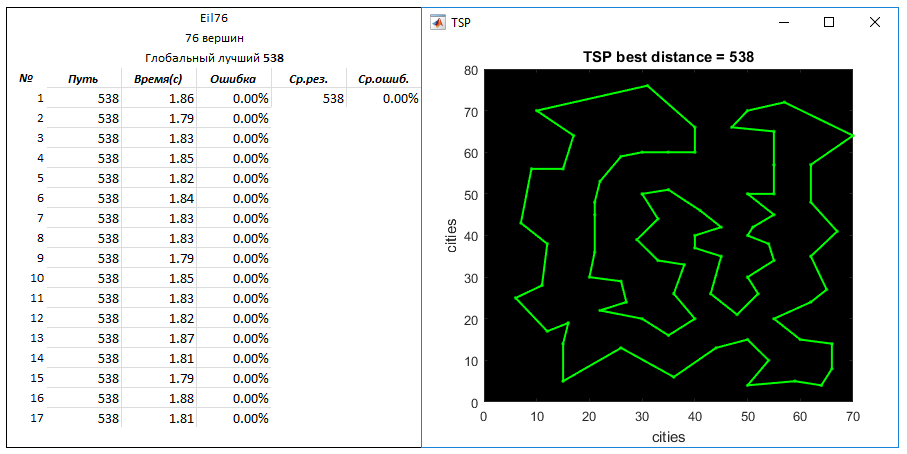
Задача Eil101 (101 вершина). Глобальный лучший путь — 629
Параметры: кол-во создаваемых маршрутов на вход — 2500
q = 0.03
N = 6
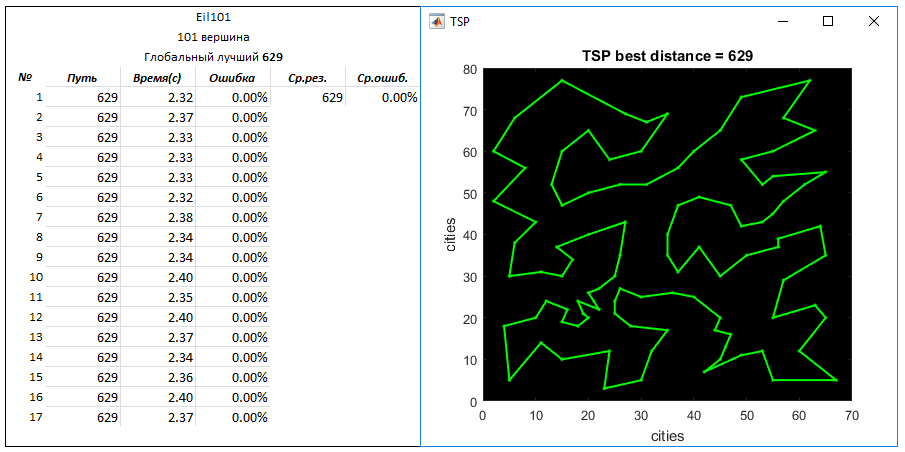
Задача Ch150 (150 вершин). Глобальный лучший путь — 6528
Параметры: кол-во создаваемых маршрутов на вход — 40000
q = 0.05
N = 10
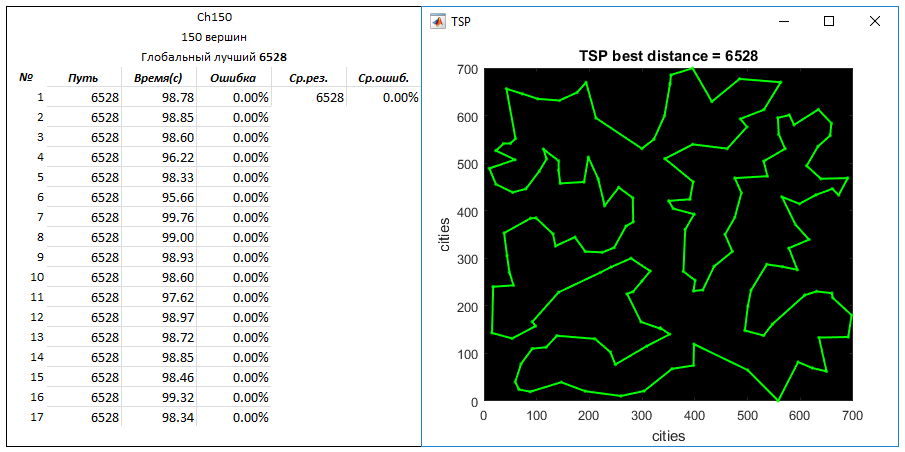
Отличный результат для годов так 2000-2005. Да, данный алгоритм намного эффективней эвристических алгоритмов, таких как метода имитации отжига или генетического алгоритма. Но согласитесь, спектр решения задач генетическим алгоритмом крайне широк, что нельзя сказать о данном алгоритме. Однако, интересно было узнать результат при смешивании различных алгоритмов.
Главная цель данного алгоритма — это создание массива оптимизированных маршрутов, также как и их массива дистанций. В следующей статье мы, с помощью данного массива, совместим генетический и муравьиный алгоритм. Задействуем вычисления на GPU. И замахнемся на нахождение глобального лучшего пути в 500, 1000 и 2000 вершин на домашнем ПК за весьма приемлемое время. Забегая вперед скажу что это вполне реально.
Итак, в данной статье мы нашли лучшие найденные пути на сегодняшний день в различных задачах. Огромная пропасть между лучшим найденным когда-либо и приближенным решением. Если данным алгоритмом находить приближенные решения, то время выполнения алгоритма будет в 10-ки раз ниже.
Ниже основной код алгоритма с комментариями (выше публиковались его функции)
% TSP() (на примере задачи коммивояжера)
%------------------------------------------------------------------------%
if exist('cities','var') == 1
clearvars -except cities
n = length(cities(:,1));
else
clearvars
intvar = inputdlg({'Кол-во вершин'}...
,'TSP',1);
n = str2double(intvar(1));
if isnan(n) || n < 0
msgbox 'Введите корректные значения'
return
else
cities = rand(n,2)*100;
end
end
% начало счетчика времени алгоритма
tic
%-------------------------------Параметры--------------------------------%
% старт с определенного города (номер строки x и y координат)
start_tour = 1;
% проверка на уникальность маршрутов, перестроение маршрутов с первых
% городов (для проверки корректности алгоритма)
check_routes = false;
% использование метода рулетки при выбора определенного города
roulete_method = false;
% метод рулетки (кол-во маршрутов)
if roulete_method == true
crrm = 1000;
end
% метод рулетки для топ "ts" кратчайших путей
top_roulete_method = true;
if top_roulete_method == true
% кол-во создаваемых маршрутов методом "топ рулетки"
ctrrm = 1000;
% выбор топ самых привлекательных городов для перехода
ts = 10;
% вероятность принятия альтернативного решения
p_change = 0.05;
end
%--------------------------------Память----------------------------------%
% матрица расстояний между городами
dist = zeros(n,n);
% лучший маршрут (расстояние)
best_dist = inf;
% массив маршрутов на вход функции brute_edge
arr_route_in = zeros(n,n);
% бета - коэффициент (на доработку)
% b = 1;
%------------------------------------------------------------------------%
% матрица расстояний
for i = 1:n
for j = 1:n
dist(i,j) = sqrt((cities(i,1) - cities(j,1))^2 + ...
(cities(i,2) - cities(j,2))^2);
end
end
% округление матрицы дистанций
dist = round(dist);
% матрица обратных расстояний
returndist = 1./dist;
% генерируем стартовый маршрут (алгоритм ближайшего соседа)
start_route = linspace(1,n,n);
% стартовый маршрут с определенного города
if start_tour > n || start_tour < 1
start_tour = 1;
end
% перестраиваем стартовый маршрут с определнного города "start_tour"
start_route(start_tour) = 1; start_route(1) = start_tour;
% создаем массив маршрутов методом ближайшего соседа
% стартуем с каждого последующего города
% parfor - параллельный цикл
parfor k = 1:n
% временная матрица (выгорает при посещении вершины)
dist_temp = dist;
% маршрут по ближайшим городам
route = zeros(1,n);
% первая стартовая позиция
next_point = start_route(k);
% заполнение маршрута
route(1) = next_point;
% посещаем каждый ближайший город
for e = 2:n
% выгорание матрицы
dist_temp(next_point,:) = nan;
% поиск ближайшего оставшегося города
[~,next_point] = min(dist_temp(:,next_point));
% заполнение маршрута
route(e) = next_point;
end
% првоеряем на уникальность и перестраиваем маршруты с 1-ого города
if check_routes == true
route = check_tour(route);
end
% массив машрутов
arr_route_in(k,:) = route;
end
% создаем массив маршрутов методом топ ближайших соседей (методом рулетки)
% вероятность посещения вершины обратно пропорциональна длине ребра
if top_roulete_method == true
arr_several = psr(dist,ctrrm,n,ts,check_routes,p_change);
arr_route_in = [arr_route_in; arr_several];
end
% создаем массив маршрутов методом рулетки
% вероятность посещения вершины обратно пропорциональна длине ребра
if roulete_method == true
% получаем массив маршрутов, выбором рулетки
[randRoute] = prr(returndist,crrm,n,check_routes);
% совмещаем два массива путей
arr_route_in = [arr_route_in;randRoute];
end
% % перестраиваем маршруты с первого города
% parfor r = 1:size(arr_route_in, 1);
% temp_route = arr_route_in(r,:);
% [~,numb_ix] = find(temp_route == 1);
% if numb_ix ~= 1
% temp_route = [temp_route(numb_ix:end),temp_route(1:numb_ix-1)];
% elseif numb_ix == n
% temp_route = fliplr(temp_route);
% end
% arr_route_in(r,:) = temp_route;
% end
% если есть, удаляем дубликаты маршрутов
arr_route_in = unique(arr_route_in,'rows');
%--------------------------------Память----------------------------------%
% массив дистанций с учетом оптимизаций (выход)
arr_tour_out = zeros(size(arr_route_in,1),n);
% массив результатов с учетом оптимизаций (выход)
arr_result = zeros(size(arr_route_in,1),1);
%------------------------------------------------------------------------%
% параллельное вычисление маршрутов (модернизированная оптимизация)
spdvar = size(arr_route_in, 1);
parfor i = 1:spdvar
% [tour, distance] = all_brute_first(dist,arr_route_in(i,:),n);
[tour, distance] = all_brute_best(dist,arr_route_in(i,:),n);
arr_tour_out(i,:) = tour;
arr_result(i,1) = distance;
end
% конец счетчика времени алгоритма
toc
% лучшая найденная дистанция
[best_length,best_indx] = min(arr_result);
% перестраиваем лучший маршрут с 1-ого города
best_route = arr_tour_out(best_indx,:);
% % среднее значение результатов
% mean(arr_result)
%-------------------------------Графика----------------------------------%
tsp_plot = figure(1);
set(tsp_plot,'name','TSP','numbertitle','off'...
,'color','w','menubar','none')
set(gcf,'position',[2391 410 476 409]);
opt_tour(:,[1,2]) = cities(best_route,[1,2]);
plot([opt_tour(:,1);opt_tour(1,1)],[opt_tour(:,2);opt_tour(1,2)],'-g.', ...
'linewidth',1.5)
set(gca,'color','k')
title(['TSP best distance = ',num2str(round(best_length,2))])
xlabel('cities');
ylabel('cities')
%------------------------------------------------------------------------%
fprintf('%s %dn','Лучшая дистанция равна',round(best_length));
clearvars -except cities arr_result arr_tour_out arr_route_in ...
n best_length opt_tour dist openclose
Спасибо за внимание. До новых встреч.
Автор: Юрий



