Кейси Муратори — один из программистов игры The Witness. В процессе разработки игры он публиковал в своём блоге посты о технических задачах, которые перед ним вставали. Ниже представлен перевод одного из таких постов.
На протяжении всей моей карьеры программиста неизменным оставался один принцип: я всегда уделяю время тому, чтобы спросить себя — почему я делаю что-то именно так, как делаю? Это происходило всегда, от создания простых программных конструкций до высокоуровневых алгоритмов. Даже глубоко укоренившиеся идеи часто бывают ошибочными, и подвергая эти идеи сомнениям, мы можем прийти к удивительным и важным открытиям.
Поэтому когда я работаю над чем-нибудь, я рефлексивно начинаю рассматривать скрывающиеся за этим причины. И высаживание травы тоже не стало исключением.
Код, описанный мной на прошлой неделе, уже встроен в дерево исходников The Witness вместе с множеством других не связанных с ним модификаций системы травы, о которых я расскажу на следующей неделе. Это было разумное решение очевидной проблемы, а времени было в обрез, поэтому я знал, что тогда было не до решения более глубоких вопросов. Но в голове я сделал мысленную заметку о том, что в следующий раз при работе над генерацией паттернов, мне нужно задаться вопросом «почему». Благодаря времени, выделенному на написание этой статьи, я получил такую возможность.
Вопрос «почему» в этом случае достаточно прост: почему мы используем для размещения травы синий шум?
Синий шум — это отличный шумовой паттерн. Как я упоминал в первой статье о траве, у него есть приятные глазу свойства. Но когда я изменил систему травы The Witness для более эффективного создания синего шума, я просто повторил за тем, кто писал код изначально. Но кто сказал, что он принял хорошее решение, выбрав синий шум? Какую именно задачу он хотел решить, и был ли синий шум лучшим решением? В прошлом я использовал синий шум для таких вещей, как трава, но был ли я уверен, что в нынешних условиях он будет оптимальной стратегией расположения?
Когда я писал предыдущие две статьи и код, который применялся для генерирования этих схем, я осознал, что ответами на эти вопросы скорее всего является «нет». Я намекал на это в предыдущей статье, когда говорил, что у нашего подхода есть теоретическая проблема, и теперь я могу чётко сказать, в чём заключается эта проблема, после чего вернусь к попыткам её решения.
Ряды кукурузы
Вот несколько скриншотов паттернов, созданных исходными техниками грубого перебора и сэмплирования соседей, которые я обсуждал ранее:
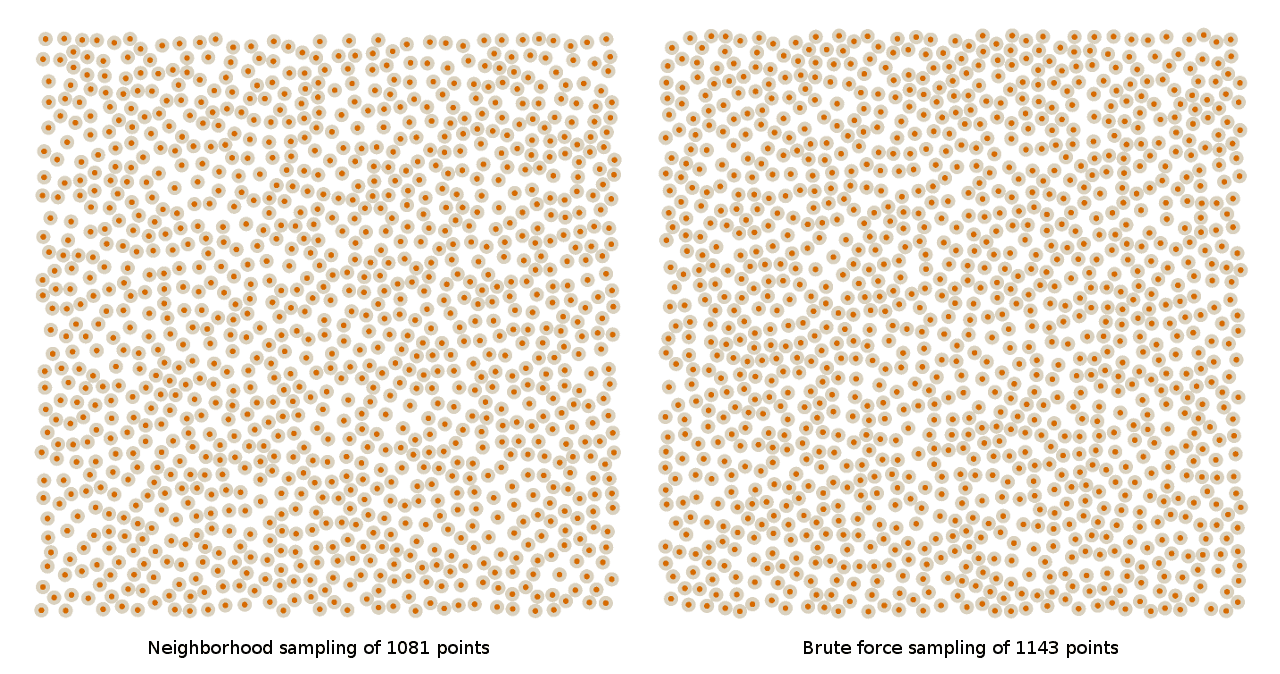
Вот как эти паттерны выглядят с точки зрения обычного игрока:
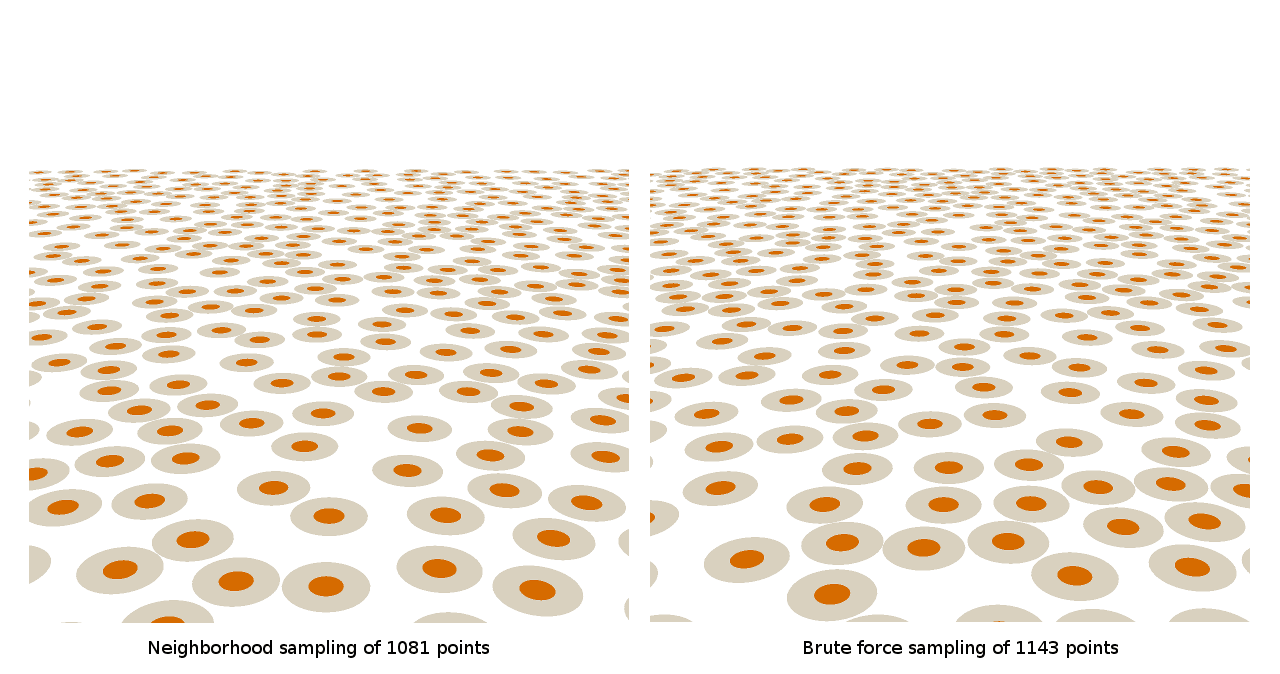
А вот, наконец, как выглядят паттерны, в каждой точке которых расположены биллборды флоры:

Как видите, большой разницы между ними нет, то есть мы проделали хорошую работу и создали алгоритм грубого перебора, который сможет достаточно быстро работать в The Witness. Но если посмотреть на эти скриншоты чуть дольше, то можно увидеть, что немного сложно понять, насколько в целом хорош синий шум. На самом деле, я понятия не имею, насколько плохи или хороши эти паттерны. У нас нет никакой отправной точки, с которой мы могли бы сравнивать подобные изображения. Как можно сказать, насколько хорош паттерн без какой-то известной схемы, создающей более качественные результаты?
Интуитивно мне казалось, что синий шум достаточно эффективно покрывает пространство. На более высоком уровне задача распределения травы может быть сформулирована как «использовать минимальное количество точек для создания визуально приятного покрытия нужной области». Я говорю «минимальное количество точек» потому что, как и в случае любой другой задачи рендеринга в реальном времени, чем меньше нужно точек для адекватного с визуальной точки зрения покрытия пространства, тем меньше затрат придётся на рендеринг травы в каждом кадре. Чем меньше затрат, тем больше остаётся сил графической системы для рендеринга других вещей. А в The Witness есть куча других вещей, которые нужно рендерить в каждом кадре, уж поверьте мне.
Поэтому да, если бы мне не нравилось заполнение в некоторых местах, я всегда мог быть увеличить плотность синего шума, потратив больше мощностей рендеринга, но получая более плотное покрытие:

Но очевидно, что нужно стремиться как можно меньшей плотности, и при этом создавать убедительное покрытие, поэтому я понимал, что нужный уровень должен быть похож на первые скриншоты статьи. Без излишнего количества точек возможно не удастся избежать пустых пятен рядом с игроком, но чуть дальше от него идеальный паттерн сделает траву красивой и насыщенной.
Однако, когда я экспериментировал на прошлой неделе с паттернами, то заметил очень неприятную вещь. В одном и том же паттерне при повороте камеры в определённые точки части паттерна создают почти ровные ряды, и очевидные пустоты заметны даже вдалеке от камеры, где в идеале должно быть достаточно перекрывающей друг друга растительности:

Это заметно при использовании обеих техник, поэтому похоже на свойство синего шума в целом, или по крайней мере всех видов синего шума, сгенерированного способом пятна Пуассона.
По причинам, которые я не буду сейчас раскрывать, мне пришлось потратить какое-то время, сидя на заднем сиденье автомобиля в Небраске, путешествуя по самой скучной автостраде в мире (так можно назвать почти любую дорогу в Небраске). Если посмотреть из окна на кукурузные поля, то можно заметить, что ряды кукурузы имеют одинаковое свойство: со множества углов они выглядят как кукурузные поля, но взглянув под правильным углом, мы увидим, что они внезапно становятся очень повторяющимися. Видны длинные и узкие разрывы между рядами. Это вполне нормально для кукурузного поля, но не совсем хорошо, когда нужно создать иллюзию плотно растущей травы.
Из-за похожести на такое свойство кукурузного поля я назвал эту проблему с синим шумом «проблемой Небраски».
Я не хотел, чтобы проблема Небраски мешала распределению травы. Насколько мне известно, это теоретическая проблема, потому что в самих алгоритмах синего шума нет ничего ошибочного. В этом случае практика абсолютно правильна, неадекватна только теория.
Поскольку я не знал теории шума, которая могла бы справиться с этой проблемой и даже не встречал статей, которые бы упоминали о её существовании, я решил поэкспериментировать с нарушением правил синего шума, чтобы проверить, смогу ли решить проблему Небраски самостоятельно.
Экспериментируем с коэффициентом упаковки
Каждый раз, когда я начинаю исследовать новую задачу, у меня нет о ней чёткого представления. Я понимаю, что проблема существует, но она ещё не определена конкретно, поэтому я случайным образом пробую очевидные вещи.
Первое, что я попробовал — изменил способ выбора точек алгоритмом подбора соседей. В предыдущей статье я не вдавался в подробности того, как этот алгоритм выбирает проверяемые точки. Я просто сделал так, чтобы он брал случайную точку «от r до 2r» в случайном направлении от базовой точки.
Это можно делать разными способами. Самый простой — единообразно выбирать угол и расстояние в интервале от r до 2r и непосредственно использовать их. Но если наносить выбранные таким образом точки, то можно увидеть, что у них есть заметное отклонение к центру окружности:
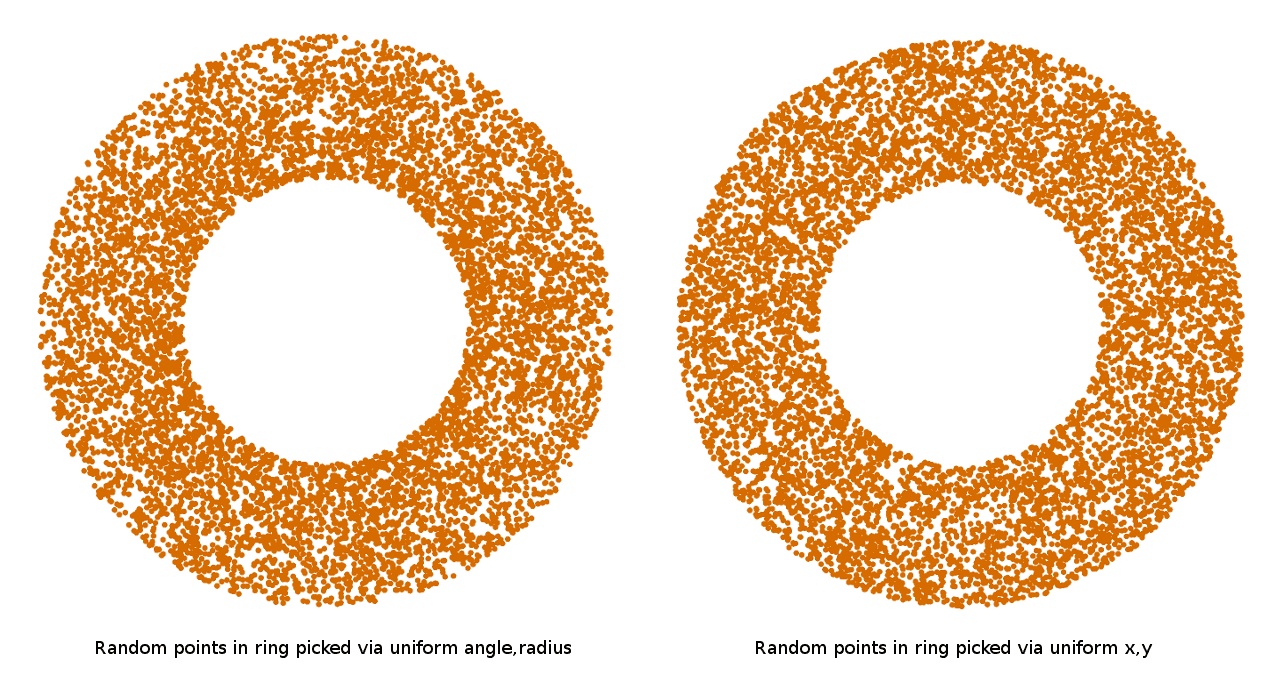
Что здесь происходит? Если задуматься об этом, то становится понятно, что чем больше радиус окружности, тем дальше перемещается точка на окружности при изменении угла. Это значит, что для покрытия периметра больших окружностей с той же евклидовой плотностью случайных точек, нам нужно брать больше случайных углов, чем при покрытии маленьких окружностей. То есть если единообразно брать случайный угол и случайный радиус, то в результате меньшие радиусы всегда будут покрыты плотнее, чем большие. Чтобы действительно подбирать точки с равномерной плотностью внутри окружности, то нужно или подбирать угол и радиус не единообразно, чтобы учитывать меняющееся влияние угла при увеличении радиуса, или, что более просто, можно просто единообразно подбирать точки в квадрате и отбрасывать те, которые не попадают в круг.
Ну хорошо, так зачем же я об этом говорю? При реализации алгоритма подбора соседей я обычно оставляю смещённость при приближении к центру. Так получается быстрее, и оказалось, что визуально это не влияет на готовый паттерн. Но так как моя задача заключалась в изменении паттерна, мне пришлось подумать — что, если принудительно сделать выборку точек ещё более смещённой?
Поэтому я решил ввести концепцию «коэффициента упаковки». Вместо подбора точек в промежутке на расстоянии от r до 2r от базовой точки, я сделал параметр равным 2. Таким образом я могу заставить все выбранные точки быть ближе к базовым точкам, теоретически снижая среднее расстояние паттерна и создавая более плотную упаковку:

К сожалению, эта попытка быстро доказала свою бесплодность, потому что плотная упаковка ещё больше подчеркнула проблему Небраски. Если посмотреть на паттерны, то можно это понять: когда упаковка становится плотнее, увеличивается вероятность того, что две «ветви» алгоритма подбора соседей будут выполняться параллельно друг другу без возможности создания более стохастических паттернов, разбавляющих пустое пространство в промежутках.
Рассматриваем пробелы
Итак, эксперименты с упаковкой оказались непродуктивными и это было логично. Я начал думать, что, возможно, недостаточно позволить точкам более гибко располагаться в пространствах, которые не заполнены плотно. Возможно, если я сделаю второй проход поверх изначального паттерна синего шума с более свободным радиусом размещения, то смогу заполнить места, в которых выровненные ряды создают заметные пробелы:

Оказалось, что это на самом деле работает. По крайней мере, так показалось на первый взгляд. Но когда я посчитал количество точек, я понял, что на самом деле если просто создать паттерн синего шума с тем же количеством точек, что и при заполнении пробелов, то он тоже будет достаточно плотным и не позволит избежать проблемы:

То есть хотя устранение пробелов в изначальном паттерне может принести плоды, я мог сразу увидеть, как заставить этот способ работать эффективно: на самом деле он увеличивал количество точек, а не устранял проблему с распределением уже имеющихся точек.
Высаживаем траву вдоль линий
Потерпев неудачу с несколькими модификациями синего шума, я начал пробовать более смехотворные подходы, у которых вообще не было свойств синего шума, просто чтобы проверить, не найдётся ли что-то интересное. Возвращаясь к первым концепциям, я думал: так, если моя цель заключается в избежании линий обзора с пробелами, то возможно стоит генерировать паттерн на основании этого принципа. Поэтому я написал алгоритм, подбиравший в области случайные линии видимости. Он проходил по каждой из линий и искал длины линий, по которым проходил определённое расстояние, не встречая точек:

К сожалению, так как алгоритм выбирает случайные линии, он вполне может выбрать две линии прямо рядом друг с другом, что снова возвращает нас к проблеме Небраски. В некоторых частях паттерна он работает вполне хорошо, но в тех частях, где линии оказываются приблизительно параллельными, проблема Небраски проявляется в полную силу.
Селективное удаление
Аналогично предыдущему способу я подумал, что, возможно, стоит попробовать обратный подход: начать с плотного покрытия области, сгенерированного белым шумом, а потом удалять только те точки, которые точно не создают длинных непрерывных линий пустого пространства. Каждая точка должна была проверяться с большим количеством направлений, и алгоритм определял, где происходит первое «попадание» вдоль этих линий в прямом и обратном направлении. Если расстояние вдоль всех проверенных линий было маленьким, то я удалял эту точку. Если получающееся расстояние вдоль любой из этих линий будет слишком большим, то я оставлял точку:

К сожалению, это дало результаты, похожие на предыдущую попытку: при настройке параметров одним способом проблема Небраски пропадала, но сэмплирование было слишком плотным. При другой настройке параметров сэмплирование оказывалось слишком разреженным и повсюду появлялись заметные пробелы, даже если я намеренно пытался избежать проблемы Небраски.
В тот момент я уже должен был догадаться. что происходит, но этого не случилось. Стоит учесть, что скорее всего это было в середине среды и я понимал, что ни за что не успею до своего дедлайна среды Witness, поэтому начал немного психовать. Я думаю недостаточно чётко. Что мне делать? Продолжать ли мне напирать или просто позвонить и сказать: «так, у меня есть проблема с алгоритмом, и будь я проклят, если знаю, как её решать. Хорошей вам среды. РОЖДЕСТВО ОТМЕНЯЕТСЯ!».
Я знаю, как важен для вас всех Санта-Клаус. Не каждый день толстый постоянно улыбающийся бородатый дед тайком проникает в дом и оставляет «подарки» для ваших детей, за которыми он «следил» весь год. Вы на самом деле хотели бы стать человеком, отменившим Рождество?
Нет, конечно же нет, и я решил — Рождество нельзя отменить. Рождество не отменяется. РОЖДЕСТВО ПРОСТО СЛЕГКА ОТКЛАДЫВАЕТСЯ.
Релаксация
Так, ну ладно, никаких проблем. Рождество откладывается. Была среда, так что оно, возможно, состоится в четверг. Или в пятницу. Возвращаемся к работе.
Если вы читали статьи по исследованиям графики, то наверно согласитесь с тем, что я скажу: если люди попадают в ситуацию, когда алгоритм очевидно просто не работает, то обязательно нужно выполнить релаксацию. Не можешь расположить точки там, где они нужны? Релаксируй! Если не можешь найти способ поставить точки там, где они необходимы, позволь им разобраться в этом самим.
Поэтому я добавил этап релаксации. И попробовал использовать для релаксации две разные «функции энергии», первая из которых была простой версией «отгоняй от себя другие точки»:

Вторая была версией «разбивай соседние линии»: она искала наборы из трёх и более точек, находящихся примерно на одной линии, и пыталась переместить одну из внутренних точек в направлении стороны, с которой было больше открытого пространства:

Как можно видеть из иллюстраций, ни одна из этих стратегий не выглядела обещающе. Хотя они были совершенно ситуативными и я мог настраивать её для получения более качественных результатов, я не увидел в предварительных результатах ничего, что говорило бы о большом смысле в стратегиях релаксации. Казалось, что как бы я ни пытался перемещать точки, они в результате случайным образом создавали новые кукурузные ряды, даже если я разбивал старые, или же пробелы между ними оказывались слишком большими, что было ещё хуже.
Это был вечер среды, и настало время ужина. Но это была необычная среда, поэтому и ужин тоже должен был стать необычным. На самом деле, это была Безумная Среда, то есть настало время безумного ужина среды.
Ограничения по направлениям
Безумная Среда — это особый день недели (часто они случаются даже не по средам, но я не буду говорить, почему), когда Шон Барретт, Фэбиен Гисен, Джефф Робертс и я собираемся, чтобы совершенно безумно провести время: четыре программиста сидят вокруг столика в ресторане и в течение часа обсуждают подробности конкретной технической проблемы. И если это звучит для вас недостаточно безумно, то конкретно в ту Безумную Среду у нас был особый гость — Томми Рефенес, поэтому я знал, что она будет ещё более Безумной, чем раньше.
Посещение Безумной Среды будет полезным, потому что я смогу обсудить проблему с другими ребятами, и, возможно, у меня появится свежий взгляд. Так и случилось.
После того, как я объяснил им проблему, Фэбиен и Шон пришли к заключению, что в первую очередь лучше всего препятствовать исходному алгоритму подбора соседей создавать линии, таким образом избежав задачи по исправлению паттерна. Если исходный алгоритм случайной генерации не будет создавать ряды, то в результате можно получить паттерны лучше, чем после исправления рядов после процесса, потому что устранение рядов — это глобальная проблема: нужно перемещать точки так, что паттерн при таком изменении может сильно изменяться. Если не создавать рядов изначально, то весь паттерн будет безрядным, то есть глобальная проблема просто исчезает.
Поэтому я попробовал эвристики для предотвращения создания линий, например, сделав так, чтобы каждая новая точка никогда не находилась бы вдоль той же линии, что и предыдущая:
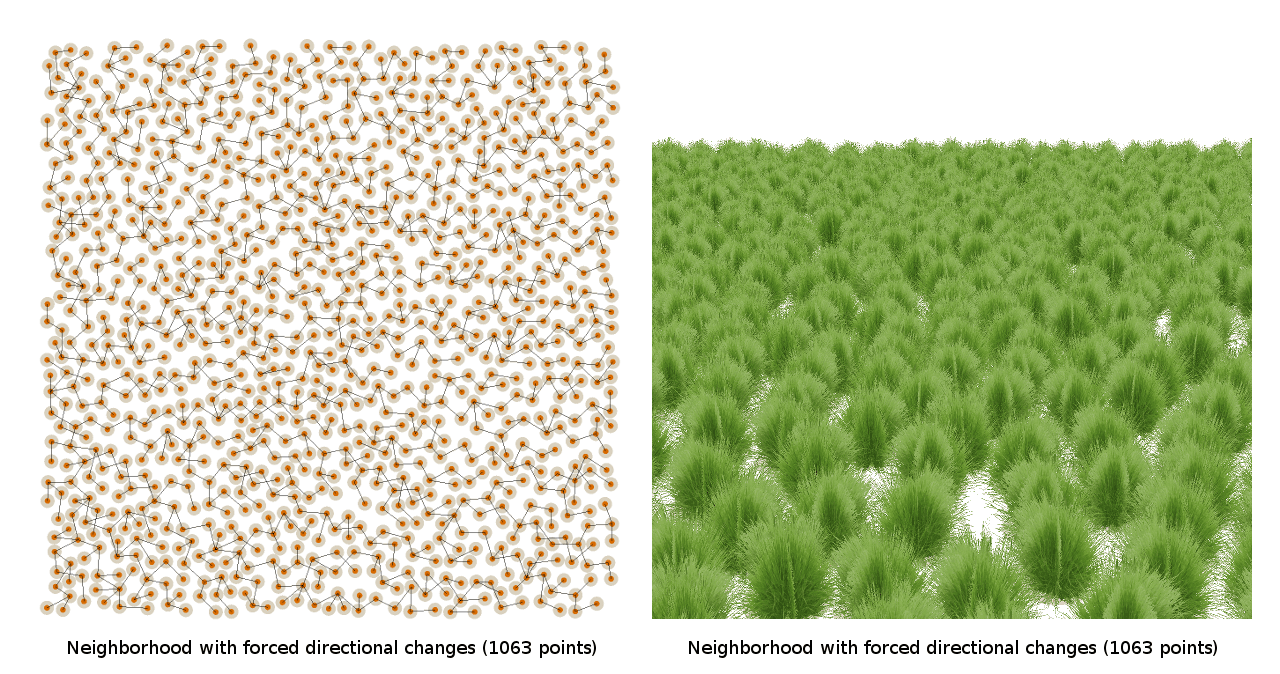
К сожалению, я всё равно получал проблему Небраски. Даже никакая непосредственная ветвь алгоритма подбора соседей не создавала рядов, похоже, соседние ветви сговаривались между собой и всё равно создавали ряды!
Это уже начинало становиться смешным. Как получается, что каждый алгоритм даёт один и тот же артефакт? Что происходит?
Искривлённая шестигранная упаковка
Хотя меня всё ещё не настигло серьёзное озарение, я начал понимать, в чём ошибка. Я сделал шаг назад и задумался о том, что может быть необходимым для создания паттерна без кукурузных рядов, который бы не использовал слишком большого количества точек. Я стал приходить к выводу, что на самом деле мне нужны кривые. Я хотел сделать так, чтобы генерируемые линии всегда придавали точкам изгибы, потому что два кривых ряда точек — это тот паттерн, в котором никогда не будет видно линейных пробелов. Любая случайная расстановка на самом деле может создать взаимное влияние точек, создающее соседние линии, даже на каждой из сторон всего по три точки — этого достаточно, чтобы проявилась проблема Небраски. Поэтому алгоритм, создающий гарантированное отсутствие пробелов, возможно, вообще не случаен, а постоянен.
Это полностью изменило мой подход к проблеме. Всё это время я думал, что для хорошего покрытия обязательна случайность. Но теперь, после тщательного обдумывания задачи, мне казалось, что случайность на самом деле может быть плохой.
Поэтому я начал размышлять о повторяющихся паттернах, которые могут иметь необходимые мне свойства. Они должны были выглядеть не очевидно повторяющимися при взгляде с точки зрения обычного игрока (стоящего в траве). В них не должны присутствовать непрерывные прямые линии точек. Они должны эффективно покрывать пространство.
Я знал, что наиболее плотной упаковкой для кругов обладают шестиугольные упаковки:

Поэтому я решил, что если нам нужно эффективно покрыть пространство, то вероятно, лучше всего начать с шестигранной упаковки, потому что она расположит каждую точку на расстоянии, визуально оптимального для покрытия, в то же время минимизируя количество используемых точек.
Но сами по себе шестигранные упаковки очевидно ужасны, потому что это кукурузные ряды в разных направлениях, то есть совсем не то, что мне нужно. Поэтому я подумал — а что, если изогнуть шестигранную упаковку? Я попробовал интерпретировать шестигранную упаковку в полярных координатах, чтобы получить ряды изогнутой формы:

Также я попробовал различные схемы поворотов, похожие на исходный алгоритм подбора соседей, в которых я ответвлял новые точки в шестигранном паттерне, которые поворачивались случайным или постоянным образом.
К сожалению, шестигранные упаковки тоже не сработали. Они или оставляли пробелы, или создавали скученности, или составляли линии в одном из направлений. Но, к счастью, именно они открыли мне глаза на то, в чём же именно заключается моя цель.
Смотрите — распределение выполняется на плоскости. На плоскости всегда есть два ортогональных базиса. Поэтому использование одной оси кривизны, которую я применял для искривления шестигранной упаковки с помощью полярных координат, ни за что бы не подошло: я искривлял бы одну из осей, вдоль которой могли создаваться линии, но не другую. На самом деле мне нужно было распределение точек с двумя осями кривизны, чтобы в буквальном смысле не оставалось возможностей для создания линий в пространстве с любой периодичностью.
Смещённая концентрическая упаковка пересечений
Ну ладно, две оси кривизны, никаких проблем. Я просто возьму две окружности и расположу точки по моему паттерну, в котором пересекаются концентрические кольца этих окружностей:

Это выглядело красиво. Я чувствовал, что могу уже быть близок к решению. Рассматривая распределение под разными углами, я увидел, что основная проблема заключалась в том, что кривизна всё равно оставалась видимой, потому что она была немного слабой для того, чтобы визуально скрыть пространство между точками. Я думал о том, что можно увеличить кривизну, но потом подумал — а что если, допустим, буду смещать каждое третье концентрическое кольцо окружности? Вместо равномерно распределённых концентрических колец радиус каждого третьего кольца будет немного смещён для внесения шума, а также немного снизить заметную повторяемость паттерна. Напоминаю, что это полностью детерминированное смещение, то есть на самом деле случайности нет:

Бинго. Именно такое покрытие мне и нужно! Плотное видимое покрытие и абсолютная невозможность заметить пробелы за исключением того места, где вы стоите (что, разумеется, никак не исправить никаким паттерном, кроме как увеличением количества точек и в буквальном смысле полным покрытием пространства). Удалось полностью устранить проблемные области обзора, которые появлялись в алгоритме без смещений:

Есть ещё и бонус — можно использовать гораздо меньше точек, чем я брал для синего шума с пробелами, получать визуально более качественное покрытие:

Почему так много неудач?
Как и в случае большинства сложных проблем, когда ты погружаешься в неё, то часто не можешь подобрать правильный взгляд на вещи. Именно поэтому это и называется «погружаться». Как бы то ни было, оглядываясь на предыдущие несколько дней, я вижу фундаментальную ошибку своего подхода.
Я начал с довольно хорошего случайного покрытия — с синего шума, и хотел усовершенствовать его. Но если вспомнить, что такое случайность и как она работает, то можно осознать довольно очевидную истину: случайность никогда не оптимальна. Для любого множества критериев чрезвычайно мала вероятность того, что можно подобрать случайным образом множество оптимальных входных данных. Если взять 100 кубиков и бросить их, то вы не получите 600. Возможно никогда (можно конечно использовать кости D20, но я хочу, чтобы эта метафора была понятна и не играющим в D&D). Также невозможно никаким образом ограничить случайность. Даже если взять все кубики и заменить все единицы, двойки, тройки и четвёрки на шестёрки, то есть на кубике останутся только пятёрки и шестёрки, то вы всё равно почти никогда не выбросите 600. Даже если сделать так и перебросить все пятёрки, то придётся делать это семь раз, пока не получите все шестёрки.
Поэтому если вы хотите сделать что-то оптимальное, то существует вероятность, что придётся пойти дальше случайных алгоритмов. Я продолжал искать схемы, которые могут создавать из случайности оптимальность, но это было очень маловероятно. Поскольку синий шум является довольно хорошим для моих целей паттерном, я пытался найти перелом в случайности, и каждая схема была обречена на провал, потому что просто не существует более хорошей случайной схемы. Чтобы совершить этот скачок, мне пришлось перейти от хаоса к порядку и непосредственно управлять оптимумом.
На самом деле это очень важный урок, который можно извлечь из этого опыта. Сам по себе паттерн не так важен. Важно понять, связана ли твоя задача с оптимизацией, и если это так, то нужно ли по каким-то другим причинам использовать случайность? Если да, то придётся выбирать что-то меньше, чем оптимальное. Если вы этого не сделаете, то чтобы двигаться дальше, придётся отказаться от случайности.
Как это бывает со многими открытиями, если подумать, то это довольно просто и практически объясняет само себя. Но часто приходится столкнуться с реальным опытом, чтобы это осело у тебя в голове и ты мог инстинктивно понимать это и применять в новых условиях, где это будет полезно.
Ниндзя, ловящий червей
Так чему же мы научились, ниндзя программирования? Думаю, тому, что, как говорит пословица, «настойчивый ниндзя всегда ловит червя». Если эта поговорка вам незнакома, то вы скорее всего не так хорошо знаете историческую японскую литературу, как я. И это нормально. Лето уже близко, и вы можете внести в свой летний список чтения кембриджский курс по истории Японии.
Мне кажется, что в моём случае ловли червя ситуация с паттернами стала моей одержимостью. Я не знаю точно, будет ли необходимо применять новый паттерн в играх, и не уверен, стоит ли использовать его в The Witness из-за потенциальных проблем работы с другой растительностью. Но как я объяснял в предыдущем разделе, я многому научился из этого опыта, как это всегда случается, когда я приступаю к технической задаче и отказываюсь сдаваться.
Для меня работа над такими задачами редко связана с действительной необходимостью нахождения решения. Я знал, что для «достаточно хороших» результатов достаточно синего шума. Но если у меня есть ощущение, что существует «более хорошее» решение, скрывающееся за «достаточно хорошим», то я обычно стремлюсь найти его. В этом случае я очень рад, что мне это удалось, потому что он открыл для меня новый способ размышления о паттернах. И я подозреваю, что даже если я и не буду использовать в будущем этот паттерн, моё более глубокое понимание различия повторяющихся и случайных паттернов даст свои дивиденды во множестве других ситуаций.
Автор: PatientZero