
Думаю, что многим из присутствующих здесь известна игра Космические Рейнджеры. Также, я не думаю, что сильно ошибусь, если скажу, что, в значительной мере, своим очарованием эта игра обязана, фактически возрожденным ей, текстовым квестам. Некоторые из этих квестов, такие как «Цитадели» или «Лыжный курорт», вполне могут рассматриваться как самостоятельные игры.
Отношение, у меня лично, к текстовым квестам двоякое. С одной стороны, они очень интересны и невообразимо атмосферны. С другой стороны, некоторые из них, пройти совсем не просто. Квест «Пятнашки», сразу поставил меня в тупик. Я вообще не очень хорошо решаю всякого рода головоломки, поэтому решил написать программу, которая найдет решение за меня.
Итак, по условиям задания, нам необходимо открыть сейф, для чего требуется решить головоломку, до боли напоминающую всем известную игру 15.

Несмотря на сходство, имеется два важных отличия, о которых следует упомянуть:
- Головоломку требуется решить за ограниченное число ходов
- Как можно заметить, цифры на фишках повторяются
Ограничение на количество ходов, как будет показано ниже, поможет нам в решении задачи (замечу, что не требуется искать кратчайшее решение, достаточно найти любое решение не превышающее 59 ходов). Со вторым пунктом все не так просто. На первый взгляд, он должен упростить решение, но это не так.
Широко известен тот факт, что половина возможных позиций в игре «15» не имеет решений. Кроме того, для части позиций, минимальное количество ходов необходимых для решения, может превысить количество ходов, заданное в условиях задания. Таким образом, если мы начнем двигать одну из парных фишек не на свое место, мы, скорее всего, не сможем решить головоломку. Чтобы не путаться с парными фишками, имеет смысл их перенумеровать, уникальным образом, сведя головоломку к классической игре «15».
Поскольку, по условиям задания, имеется 7 пар совпадающих фишек, фактически требуется решить одну из 2^(7 — 1) = 64 головоломок, часть которых не будет иметь решения. Это несомненно усложняет задачу.
Прежде чем приступать к решению задачи, заметим, что требуется хранить состояние 16 клеток, каждая из которых может находиться в 16 состояниях (пустая клетка будет кодироваться нулем). Это позволяет использовать для хранения позиции 8-байтное целое число.
Начнем с решения классической головоломки «15» (с не повторяющимися фишками):
#ifndef SOLVER_H_
#define SOLVER_H_
#include <stdio.h>
#include "common.h"
#include "PerfCnt.h"
class Solver {
public:
Solver(Long startPos, Long endPos, int stepCnt):
startPos(startPos),
endPos(endPos),
stepCnt(stepCnt),
posCnt(0),
perfCnt() {}
bool solve();
private:
Long startPos;
Long endPos;
int stepCnt;
Long posCnt;
PerfCnt perfCnt;
static Long pos[MAX_DEEP];
static Byte step[MAX_DEEP];
void dumpSolve(int deep);
void dumpPos(int delta);
void dumpTotal();
bool checkPos(Long p, int deep);
bool solve(int deep, int delta, int startDelta, int X, int Y);
Long getStep(Long p, int x, int y, int dx, int dy, int& dd);
};
#endif
#include "solver.h"
Long Solver::pos[MAX_DEEP];
Byte Solver::step[MAX_DEEP];
void Solver::dumpPos(int delta) {
printf("Distance: %dnn", delta);
Long mask = 0xFFFF;
for (int shift = 48; shift >= 0; shift -= 16) {
int x = (int)((startPos & (mask << shift)) >> shift);
int y = (int)((endPos & (mask << shift)) >> shift);
printf("%04X %04Xn", x, y);
}
}
void Solver::dumpSolve(int deep) {
printf("n");
for (int i = 0; i < deep; i++) {
printf("%d", step[i]);
}
printf("n");
}
void Solver::dumpTotal() {
printf("nCount: %6I64dn", posCnt);
printf("Time: %7.3fnn", perfCnt.elapsed());
}
bool Solver::checkPos(Long p, int deep) {
int j = MAX_LOOP;
for (int i = deep - 1; i >=0; i--) {
if (pos[i] == p) return true;
if (--j <= 0) break;
}
return false;
}
bool Solver::solve() {
if (stepCnt >= MAX_DEEP) return false;
pos[0] = startPos;
int delta = getDelta(startPos, endPos);
int X = getX(startPos);
int Y = getY(startPos);
dumpPos(delta);
bool r = solve(0, delta, delta, X, Y);
dumpTotal();
return r;
}
Long Solver::getStep(Long p, int x, int y, int dx, int dy, int& dd) {
Long digit = getDigit(p, x + dx, y + dy);
if (digit == 0) return p;
if (dx != 0) {
int delta = getDeltaX(startPos, endPos, digit);
if (delta * dx <= 0) {
dd++;
} else {
dd--;
}
}
if (dy != 0) {
int delta = getDeltaY(startPos, endPos, digit);
if (delta * dy <= 0) {
dd++;
} else {
dd--;
}
}
xorDigit(p, x, y, digit);
xorDigit(p, x + dx, y + dy, digit);
return p;
}
bool Solver::solve(int deep, int delta, int startDelta, int X, int Y) {
if (pos[deep] == endPos) {
dumpSolve(deep);
return true;
}
if (delta > stepCnt - deep) {
return false;
}
if (delta - startDelta > MAX_DELTA_DIFF) {
return false;
}
for (int i = 0; i < 4; i++) {
int dd = 0;
int dx = 0;
int dy = 0;
switch (i) {
case 0:
dy--;
break;
case 1:
dx++;
break;
case 2:
dy++;
break;
case 3:
dx--;
break;
}
if ((X + dx < 1)||(Y + dy < 1)||(X + dx > 4)||(Y + dy > 4)) continue;
if (deep + 1 >= MAX_DEEP) return false;
pos[deep + 1] = getStep(pos[deep], X, Y, dx, dy, dd);
if (checkPos(pos[deep + 1], deep)) continue;
step[deep] = i;
posCnt++;
if (solve(deep + 1, delta + dd, startDelta, X + dx, Y + dy)) return true;
}
return false;
}
Это обыкновенный поиск с возвратом. Мы перебираем все возможные ходы, изменяем позицию и вызываем для новой позиции ту-же функцию рекурсивно. Сделанные ходы кодируем цифрами от 0 до 3, обозначающими направление перемещения пустой клетки (0 — вверх, 1 — вправо, 2 — вниз, 3 — влево):
switch (i) {
case 0:
dy--;
break;
case 1:
dx++;
break;
case 2:
dy++;
break;
case 3:
dx--;
break;
}
Для удобства вывода решения, храним последовательность выполненных ходов в стеке (поскольку количество ходов ограничено условиями задачи, можно использовать обычный статический массив).
Главная сложность такого подхода — лавинообразное нарастание количества просматриваемых позиций, в зависимости от глубины поиска. Требуется как-то отсекать ходы, заведомо не ведущие к правильному решению. В этом помогут следующие соображения:
- Для каждой позиции возможно от 2 до 4 возможных ходов (в зависимости от положения пустой клетки), при этом, не имеет смысла повторять ранее рассмотренные позиции (позиции, также как и ходы, можно хранить в статическом стеке).
- Для каждой позиции можно вычислить манхеттенское расстояние до искомой позиции (суммарное количество ходов, необходимых для возврата всех фишек на свое место, при условии, что другие фишки им не мешают). Далее по тексту, я буду называть его просто расстоянием. В случае, если вычисленное расстояние превышает количество оставшихся ходов, позиция не имеет решения и дальнейший перебор можно прекратить (здесь нам помогает знание о том, что головоломка решается не более чем за N ходов).
Поскольку вычисление расстояния относительно ресурсоемкая операция, его можно вычислить один раз (для первоначальной позиции), в дальнейшем инкрементируя или декрементируя эту величину в зависимости от направления перемещения фишки, которой делается очередной ход.
Реализуем вспомогательные функции:
#ifndef COMMON_H_
#define COMMON_H_
typedef unsigned __int64 Long;
typedef unsigned __int16 Short;
typedef unsigned char Byte;
const int MAX_POSITION = 4;
const int MAX_DIGIT = 15;
const int MAX_DEEP = 100;
const int MAX_LOOP = 10;
const int MAX_TASKS = 100;
const int MAX_DELTA_DIFF = 5;
int getPosition(Long part);
int getX(Long state);
int getY(Long state);
int getX(Long state, Long d);
int getY(Long state, Long d);
int getDeltaX(Long a, Long b, Long d);
int getDeltaY(Long a, Long b, Long d);
int getDelta(Long a, Long b);
Long getDigit(Long p, int x, int y);
void xorDigit(Long& p, int x, int y, Long d);
void setDigit(Long& p, Long m, Long d);
#endif
#include "common.h"
#include <math.h>
Long digit[MAX_DIGIT + 1] = {
0x0000000000000000L,
0x1111111111111111L,
0x2222222222222222L,
0x3333333333333333L,
0x4444444444444444L,
0x5555555555555555L,
0x6666666666666666L,
0x7777777777777777L,
0x8888888888888888L,
0x9999999999999999L,
0xAAAAAAAAAAAAAAAAL,
0xBBBBBBBBBBBBBBBBL,
0xCCCCCCCCCCCCCCCCL,
0xDDDDDDDDDDDDDDDDL,
0xEEEEEEEEEEEEEEEEL,
0xFFFFFFFFFFFFFFFFL
};
int getPosition(Long part) {
for (int i = 4; i > 0; i--) {
if ((part & 0xF) == 0) return i;
part >>= 4;
}
return 0;
}
int getX(Long state) {
for (int i = 4; i >= 1; i--) {
int r = getPosition(state & 0xFFFF);
if (r != 0) return r;
state >>= 16;
}
return 0;
}
int getY(Long state) {
for (int i = 4; i >= 1; i--) {
int r = getPosition(state & 0xFFFF);
if (r != 0) return i;
state >>= 16;
}
return 0;
}
int getX(Long state, Long d) {
state ^= digit[d];
return getX(state);
}
int getY(Long state, Long d) {
state ^= digit[d];
return getY(state);
}
int getDeltaX(Long a, Long b, Long d) {
a ^= digit[d]; b ^= digit[d];
return getX(a) - getX(b);
}
int getDeltaY(Long a, Long b, Long d) {
a ^= digit[d]; b ^= digit[d];
return getY(a) - getY(b);
}
int getDelta(Long a, Long b) {
int r = 0;
for (Long d = 1; d <= MAX_DIGIT; d++) {
r += abs(getDeltaX(a, b, d));
r += abs(getDeltaY(a, b, d));
}
return r;
}
Long getDigit(Long p, int x, int y) {
for (; y <= 4; y++) {
if (y == 4) {
p &= 0xFFFF;
for (; x <= 4; x++) {
if (x == 4) {
return p & 0xF;
}
p >>= 4;
}
break;
}
p >>= 16;
}
return -1;
}
void xorDigit(Long& p, int x, int y, Long d) {
for (; x < 4; x++) {
d <<= 4;
}
for (; y < 4; y++) {
d <<= 16;
}
p ^= d;
}
void setDigit(Long& p, Long m, Long d) {
p ^= p & m;
m &= digit[d];
p ^= m;
}
В целях оптимизации производительности, стараемся максимально использовать битовые операции.
Чтобы убедиться, что все работает, можно решить небольшую головоломку:
1 2 3 4 5 1 3 4
5 6 7 8 9 2 B 7
9 A B C D 6 A 8
D E F E F C
Поскольку я сам подготовил этот пример, я знаю, что для его решения достаточно 11 ходов.
Действительно, при таком ограничении, программа выводит ответ за тысячную долю секунды:
Distance: 11
1234 5134
5678 92B7
9ABC D6A8
DEF0 0EFC
00323003222
Count: 18
Time: 0.001
Мы видим, что рассмотрено 18 позиций. Чтобы оценить нарастание сложности, в зависимости от разности ограничения на количество ходов и расстояния до конечной позиции, я буду увеличивать ограничение на количество ходов, фиксируя количество просмотренных позиций.
Итоговый график выглядит следующим образом:
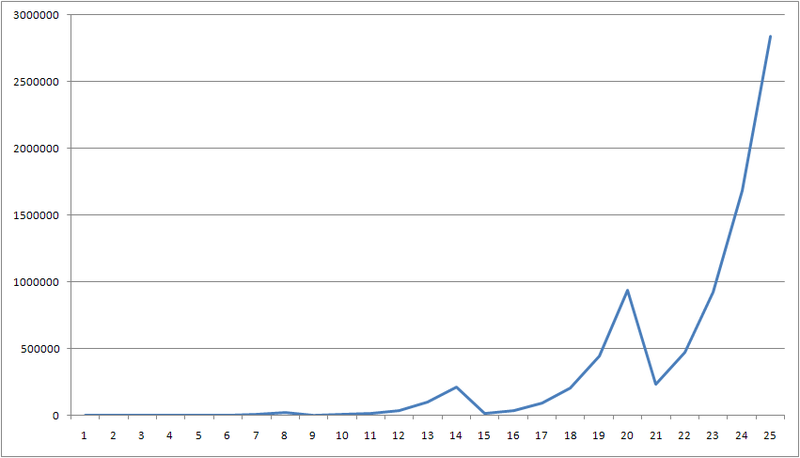
Пилообразность графика объясняется тем, что программа находит новые (более длинные) решения, при увеличении ограничения на количество ходов. Как и предполагалось, количество просматриваемых позиций возрастает очень быстро.
Теперь осталось реализовать перенумерацию парных фишек. В этом, также поможет рекурсия:
#ifndef INITIALIZER_H_
#define INITIALIZER_H_
#include "common.h"
#include "solver.h"
struct Task {
Long startPos;
Long endPos;
int delta;
bool isProcessed;
};
class Initializer {
public:
Initializer(Long startPos, Long endPos, int stepCnt):
startPos(startPos),
endPos(endPos),
stepCnt(stepCnt),
taskCnt(0) {}
bool solve();
private:
Long startPos;
Long endPos;
int stepCnt;
int taskCnt;
static Task tasks[MAX_TASKS];
static int digits[MAX_DIGIT + 1];
bool checkInit(Long s, Long e);
bool addPos(Long s, Long e);
bool init(Long s, Long e);
Long getFreeDigit();
bool checkPos(Long s, Long e);
void normalize(Long& p);
void dumpPos(Long s, Long e, int delta);
};
#endif
#include "initializer.h"
Task Initializer::tasks[MAX_TASKS];
int Initializer::digits[MAX_DIGIT + 1];
bool Initializer::solve() {
if (!init(startPos, endPos)) return false;
while (true) {
int mn = stepCnt;
int ix = -1;
for (int i = 0; i < taskCnt; i++) {
if (tasks[i].isProcessed) continue;
if (stepCnt - tasks[i].delta < mn) {
mn = stepCnt - tasks[i].delta;
ix = i;
}
}
if (ix < 0) break;
tasks[ix].isProcessed = true;
Solver solver(tasks[ix].startPos, tasks[ix].endPos, stepCnt);
if (solver.solve()) return true;
}
return false;
}
bool Initializer::checkInit(Long s, Long e) {
for (int i = 0; i <= MAX_DIGIT; i++) {
digits[i] = 0;
}
for (int i = 0; i <= MAX_DIGIT; i++) {
digits[s & 0xF]++;
s >>= 4;
}
if (digits[0] != 1) return false;
for (int i = 0; i <= MAX_DIGIT; i++) {
digits[e & 0xF]--;
e >>= 4;
}
for (int i = 0; i <= MAX_DIGIT; i++) {
if (digits[i] != 0) return false;
}
return true;
}
void Initializer::dumpPos(Long s, Long e, int delta) {
printf("0x");
Long mask = 0xFFFF;
for (int shift = 48; shift >= 0; shift -= 16) {
int x = (int)((s & (mask << shift)) >> shift);
printf("%04X", x);
}
printf(" 0x");
mask = 0xFFFF;
for (int shift = 48; shift >= 0; shift -= 16) {
int x = (int)((e & (mask << shift)) >> shift);
printf("%04X", x);
}
printf(" %dn", delta);
}
bool Initializer::addPos(Long s, Long e) {
if (!checkPos(s, e)) return true;
if (taskCnt >= MAX_TASKS) return false;
tasks[taskCnt].startPos = s;
tasks[taskCnt].endPos = e;
tasks[taskCnt].delta = getDelta(s, e);
tasks[taskCnt].isProcessed = false;
if (tasks[taskCnt].delta == 0) return false;
if (tasks[taskCnt].delta > stepCnt) return true;
taskCnt++;
return true;
}
Long Initializer::getFreeDigit() {
for (Long i = 1; i <= MAX_DIGIT; i++) {
if (digits[i] == 0) return i;
}
return 0;
}
bool Initializer::init(Long s, Long e) {
for (int i = 0; i <= MAX_DIGIT; i++) {
digits[i] = 0;
}
Long x = s;
for (int i = 0; i <= MAX_DIGIT; i++) {
digits[x & 0xF]++;
x >>= 4;
}
bool f = true;
for (int i = 0; i <= MAX_DIGIT; i++) {
if (digits[i] != 1) f = false;
}
if (f) {
return addPos(s, e);
}
Long d = getFreeDigit();
if (d == 0) return false;
x = s;
Long ms = 0xF;
for (int i = 0; i <= MAX_DIGIT; i++) {
Long t = x & 0xF;
if (digits[t] > 1) {
setDigit(s, ms, d);
Long y = e;
Long me = 0xF;
for (int j = 0; j <= MAX_DIGIT; j++) {
if ((y & 0xF) == t) {
Long k = e;
setDigit(k, me, d);
if (!init(s, k)) return false;
}
me <<= 4;
y >>= 4;
}
break;
}
ms <<= 4;
x >>= 4;
}
return true;
}
void Initializer::normalize(Long& p) {
int x = getX(p);
int y = getY(p);
for (; x < 4; x++) {
Long d = getDigit(p, x + 1, y);
xorDigit(p, x + 1, y, d);
xorDigit(p, x, y, d);
}
for (; y < 4; y++) {
Long d = getDigit(p, x, y + 1);
xorDigit(p, x, y + 1, d);
xorDigit(p, x, y, d);
}
}
bool Initializer::checkPos(Long s, Long e) {
normalize(s); normalize(e);
Long nums[16] = {0};
int ix = 0;
for (int y = 1; y < 4; y++) {
for (int x = 1; x < 4; x++) {
Long d = getDigit(e, x, y);
if (d != 0) {
nums[d] = ++ix;
}
}
}
int cn = 0;
for (int y = 1; y < 4; y++) {
for (int x = 1; x < 4; x++) {
Long d = getDigit(s, x, y);
for (Long i = 1; i <= 15; i++) {
if (nums[i] < nums[d]) {
int Y = getY(s, i);
if (Y < y) continue;
if (Y > y) {
cn++;
break;
}
int X = getX(s, i);
if (X > x) {
cn++;
break;
}
}
}
}
}
return (cn & 1) == 0;
}
Перед добавлением в список, проверяем, имеет ли позиция решение и может ли она быть решена за указанное число ходов (лучше лишний раз проверить, чем выполнять затратный поиск для позиции, заведомо не имеющей решения).
Вот список возможных позиций, отсортированный в порядке убывания расстояния:
0x763258F4E1DCBA90 0x6CBEDA1F29873450 50
0x763258F4E1DCBA90 0x6CBED81F29A73450 48
0x763258F4E1DCBA90 0x6CBEDA9F21873450 48
0x763258F4E1DCBA90 0x6CBED89F21A73450 46
0x763258F4E1DCBA90 0x6C4EDA1F29873B50 44
0x763258F4E1DCBA90 0x65BEDA12F98734C0 44
0x763258F4E1DCBA90 0x6CBE7A1F298D3450 44
0x763258F4E1DCBA90 0x6C4ED81F29A73B50 42
0x763258F4E1DCBA90 0x65BED812F9A734C0 42
0x763258F4E1DCBA90 0x6CBE781F29AD3450 42
0x763258F4E1DCBA90 0x6CB3DA1F2987E450 42
0x763258F4E1DCBA90 0x6C4EDA9F21873B50 42
0x763258F4E1DCBA90 0x65BEDA92F18734C0 42
0x763258F4E1DCBA90 0x6CBE7A9F218D3450 42
0x763258F4E1DCBA90 0x6CB3D81F29A7E450 40
0x763258F4E1DCBA90 0x6C4ED89F21A73B50 40
0x763258F4E1DCBA90 0x65BED892F1A734C0 40
0x763258F4E1DCBA90 0x6CBE789F21AD3450 40
0x763258F4E1DCBA90 0x6CB3DA9F2187E450 40
0x763258F4E1DCBA90 0x654EDA12F9873BC0 38
0x763258F4E1DCBA90 0x6C4E7A1F298D3B50 38
0x763258F4E1DCBA90 0x65BE7A12F98D34C0 38
0x763258F4E1DCBA90 0x6CB3D89F21A7E450 38
0x763258F4E1DCBA90 0x654ED812F9A73BC0 36
0x763258F4E1DCBA90 0x6C4E781F29AD3B50 36
0x763258F4E1DCBA90 0x65BE7812F9AD34C0 36
0x763258F4E1DCBA90 0x6C43DA1F2987EB50 36
0x763258F4E1DCBA90 0x65B3DA12F987E4C0 36
0x763258F4E1DCBA90 0x6CB37A1F298DE450 36
0x763258F4E1DCBA90 0x654EDA92F1873BC0 36
0x763258F4E1DCBA90 0x6C4E7A9F218D3B50 36
0x763258F4E1DCBA90 0x65BE7A92F18D34C0 36
0x763258F4E1DCBA90 0x6C43D81F29A7EB50 34
0x763258F4E1DCBA90 0x65B3D812F9A7E4C0 34
0x763258F4E1DCBA90 0x6CB3781F29ADE450 34
0x763258F4E1DCBA90 0x654ED892F1A73BC0 34
0x763258F4E1DCBA90 0x6C4E789F21AD3B50 34
0x763258F4E1DCBA90 0x65BE7892F1AD34C0 34
0x763258F4E1DCBA90 0x6C43DA9F2187EB50 34
0x763258F4E1DCBA90 0x65B3DA92F187E4C0 34
0x763258F4E1DCBA90 0x6CB37A9F218DE450 34
0x763258F4E1DCBA90 0x654E7A12F98D3BC0 32
0x763258F4E1DCBA90 0x6C43D89F21A7EB50 32
0x763258F4E1DCBA90 0x65B3D892F1A7E4C0 32
0x763258F4E1DCBA90 0x6CB3789F21ADE450 32
0x763258F4E1DCBA90 0x654E7812F9AD3BC0 30
0x763258F4E1DCBA90 0x6543DA12F987EBC0 30
0x763258F4E1DCBA90 0x6C437A1F298DEB50 30
0x763258F4E1DCBA90 0x65B37A12F98DE4C0 30
0x763258F4E1DCBA90 0x654E7A92F18D3BC0 30
0x763258F4E1DCBA90 0x6543D812F9A7EBC0 28
0x763258F4E1DCBA90 0x6C43781F29ADEB50 28
0x763258F4E1DCBA90 0x65B37812F9ADE4C0 28
0x763258F4E1DCBA90 0x654E7892F1AD3BC0 28
0x763258F4E1DCBA90 0x6543DA92F187EBC0 28
0x763258F4E1DCBA90 0x6C437A9F218DEB50 28
0x763258F4E1DCBA90 0x65B37A92F18DE4C0 28
0x763258F4E1DCBA90 0x6543D892F1A7EBC0 26
0x763258F4E1DCBA90 0x6C43789F21ADEB50 26
0x763258F4E1DCBA90 0x65B37892F1ADE4C0 26
0x763258F4E1DCBA90 0x65437A12F98DEBC0 24
0x763258F4E1DCBA90 0x65437812F9ADEBC0 22
0x763258F4E1DCBA90 0x65437A92F18DEBC0 22
0x763258F4E1DCBA90 0x65437892F1ADEBC0 20
Именно в этом порядке я начал проверять позиции, поскольку считал, что быстрее всего поиск будет выполняться для позиций, имеющих максимальное расстояние. Действительно, первые элементы списка были проверены за несколько секунд, но для первой же позиции с расстоянием 42, поиск пришлось остановить после 10 минут ожидания.
В этом месте я слегка приуныл и начал задумываться о введении эвристик для определения порядка перебора возможных ходов, да и вообще, о более внимательном изучении алгоритма A*. Но, уже просто по инерции, решил проверить последний элемент списка:
#include <iostream>
#include <tchar.h>
#include "initializer.h"
int _tmain(int argc, _TCHAR* argv[])
{
Initializer m(0x763258F4E1DCBA90, 0x65437892F1ADEBC0, 59);
m.solve();
return 0;
}
Я даже не сразу понял, что программа нашла решение:
Distance: 20
7632 6543
58F4 7892
E1DC F1AD
BA90 EBC0
00032103210321032330111223010323032112233000121221
Count: 6117348
Time: 2.404
Всего за две с половиной секунды.
Квест пройден.
Исходники, как всегда, на GitHub.
Автор: GlukKazan






