Привет!
Продолжая неделю морского боя, хочу предложить еще один способ построения оптимальной стратегии стрельбы. Он использует представление стратегии в виде дерева, что весьма распространено в теории игр. Представление задачи в виде таблицы решений позаимствовано из теории тестов, которая была популярна в 70-е годы прошлого века и применялась, в частности, для контроля и диагностики неисправностей в электронных схемах. Этот способ позволяет найти оптимальную стратегию, но у него очень большая вычислительная сложность. Увы, игру на поле 10x10 проанализировать не удалось.
Дерево решений
И когда Великобритания, а затем и Германия построили дредноуты, война между ними стала неизбежной. Потому что, кроме вопросов о тактике применения новых кораблей, на которые хоть как-то можно было ответить умозрительно, был один, ответить на который теоретически было решительно невозможно. Он звучал так: «А ЧЬИ ДРЕДНОУТЫ ЛУЧШЕ?!»
(Вольная цитата из спектакля Е. Гришковца «Дредноуты»)
Для начала обзаведемся удобным способом представления стратегии в виде дерева решений. Например, вот как можно расстрелять крейсер и два катера на поле 3x3.
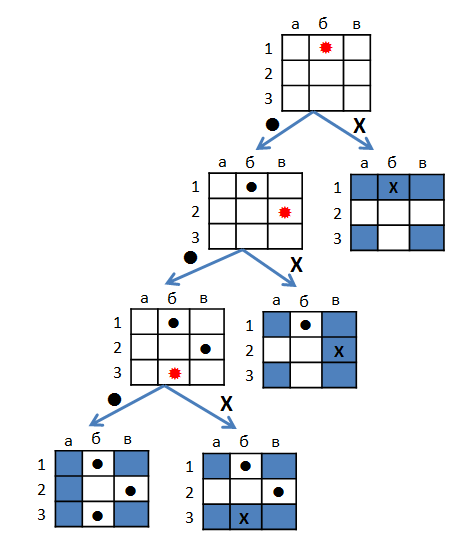
В вершинах дерева нарисовано игровое поле с уже сделанными выстрелами. Текущий выстрел отмечен красным цветом. Ребрам приписан результат выстрела: промах (.) или попадание (x). В листьях показано расположение кораблей. Стратегию можно описать словами так. Сначала стреляем в б1. Если попадаем, становится понятно как расположены корабли, и остается их добить. Если нет, стреляем в в2. Если попадаем, снова все понятно. Если промахиваемся, остается два варианта расположения, и выстрел в б3 вносит окончательную ясность.
Понятно, что так можно описать любую стратегию стрельбы, хватило бы бумаги. Но для того, чтобы найти хорошую стратегию, нужно формализовать, что мы на самом деле хотим. Заметим, что стратегия описывает действия игрока «на все случаи жизни», но конкретная игра со своим расположением кораблей описывается путем в дереве от корня до одного из листьев. Доиграв до конца и выиграв, мы попадем столько раз, сколько было труб на кораблях противника. Можно переформулировать правила так: каждый из игроков стреляет до полного уничтожения эскадры противника, а потом выигрывает тот, у кого было меньше промахов. Значит, хорошая стратегия отличается от плохой количеством промахов. И теперь у нас есть две возможности.
Можно оценивать стратегию по тому, сколько промахов будет сделано в худшем случае. Тогда из двух стратегий лучше та, у которой максимальное число промахов в пути от корня до листа минимально. А можно предположить, что противник выбирает расположение случайно с равной вероятностью, и стараться уменьшить ожидаемое число промахов. Тогда из двух стратегий будет лучше та, у которой сумма промахов во всех путях от корня каждого из листьев листа будет наименьшей. К примеру, наша стратегия позволяет гарантированно уничтожить корабли, сделав не более трех промахов, а ожидаемое число промахов равно (3+2+1+0)/4=1,5.
Кстати, можно попробовать найти стратегию, которая будет лучшей в обоих смыслах. Звучит заманчиво? Увы, обе задачи слишком похожи на NP-трудную задачу о покрытии множества, что обещает нам отсутствие легких алгоритмов решения. Но, запасшись терпением и машинным временем, попытаемся все же что-то сделать.
Таблица решений и алгоритмы построения стратегии
Давайте представим задачу в виде так называемой таблицы решений. Построим прямоугольную таблицу, в которой столбцы соответствуют клеткам игрового поля, а строки — всевозможным вариантам расположения кораблей. Ячейка таблицы на пересечении строки и столбца содержит знак «X» если в данном расположении кораблей в данной клетке игрового поля есть корабль, и "." в противном случае. К примеру, вот таблица, описывающая четыре возможных варианта расположения крейсера и двух катеров на поле 3x3 (каждой строке справа приписана клетка, в которой находится середина крейсера — в нашем примере она однозначно определяет расположение кораблей).
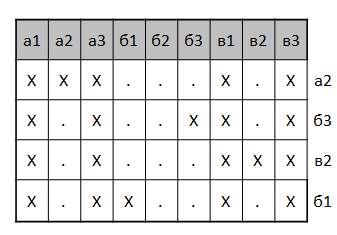
Разглядывая таблицу, можно понять, что нет смысла стрелять в б2, потому что ни в одной конфигурации там нет корабля. Выстрелы в a1, a3, в1, в3 гарантирует попадание, но не дает дополнительно информации о расположении кораблей. Их можно выполнить в начале для устрашения противника. Выстрел в каждую из оставшихся клеток при попадании однозначно определяет строку, а при промахе уменьшает число гипотез на одну. Можно представить этот процесс как вычеркивание из таблицы строк, противоречащих накопленной информации.
Приближенный жадный алгоритм строит дерево, начиная с корня. Алгоритм выбирает столбец таблицы (клетку для выстрела), так чтобы доля строк, имеющих корабль в этой клетке было как можно ближе к 1/2. Выбранная клетка приписывается корню дерева, из корня проводится два ребра, соответствующие промаху/попаданию, к концам ребер подвешиваются две новые вершины. Каждой из новых вершин достается подтаблица, в которой вычеркнуты строки, противоречащие результатам первого выстрела. К каждому из листьев применяется та же процедура до тех пор, пока все полученные таблицы не станут содержать всего одну строку. Соответствующие вершины становятся листьями, и алгоритм завершает работу.
Другой алгоритм использует динамическое программирование. Он анализирует огромный граф подтаблиц, но гарантирует, что найденное решение будет оптимальным. К сожалению, подробный рассказ о нем заслуживает отдельного поста. Я как-нибудь соберусь с силами и напишу, а сейчас предлагаю поверить в его существование и перейти к экспериментальной части.
Эксперимент
Теоретик решает, что может, как нужно, а практик — что нужно, как может.
Число конфигураций (1,85*1015), озвученное уважаемым Mrrl, застало меня в процессе написания кода и изрядно охладило мой пыл. Подумав, я решил довести дело до конца, при этом уменьшив размер поля. Точный алгоритм согласился отработать с задачей стрельбы по эскадре из одного крейсера, двух эсминцев и трех катеров на поле 5x5. Число возможных конфигураций при этом равно всего 1428, но граф подзадач состоит из впечатляющих 10 191 257 вершин и 214 464 800 ребер. Оптимальный алгоритм позволяет уничтожить эскадру, допустив не более семи промахов, а в среднем допускает 4,51 промах. На рисунке ниже показано, как можно определить положение кораблей по пяти промахам (т.е. при реализации самой правой ветки дерева решений).
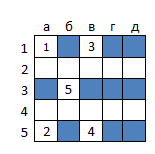
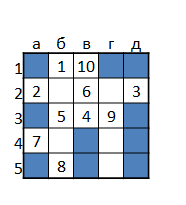
Жадный алгоритм для этой же задачи построил стратегию, допускающую 11 промахов в худшем случае, при ожидаемом числе промахов 5,46. Рисунок ниже показывает стратегию стрельбы при промахах (самую правую ветку дерева решений).
Резюме
Классический жадный алгоритм отработал скверно. Я думаю, он бы неплохо справился с минимизацией длины пути в дереве, а число промахов явно требует другой эмпирики выбора клетки для выстрела. Точный алгоритм одолел задачу с половиной кораблей на четвертинке поля, так что похвалиться особо нечем. Немного греет душу то, что для этой мелкой задачи мы теперь знаем-таки число промахов для оптимальной стратегии (7 в худшем случае, 4,51 в среднем). Буду рад, если это поможет коллегам, строящим приближенные алгоритмы.
Автор: ich76