Графы для самых маленьких: DFS и BFS

Многие объекты окружающей действительности могут быть смоделированы с использованием графов: карта метро, лабиринт, знакомства в соцсетях, возможные ходы в настольной игре — все это графы. Самое простое и частое действие, которое можно сделать с графом — это перебрать его вершины в каком-то порядке. Под катом я бы хотел рассказать про два самых известных алгоритма на графах — об обходах в глубину и в ширину.

Немного теории

Итак, что же такое граф? Это множество объектов, называемых вершинами, и некоторое подмножество их пар, называемых ребрами. Например, вот так:

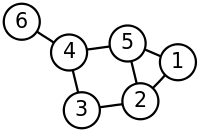
Граф может быть ориентированным или неориентированным — в первом случае предполагается, что ребро (u, v) — это не то же самое, что (v, u).

Очевидно, что добавлением обратных ребер можно превратить неориентированный граф в ориентированный, поэтому мы будем рассматривать только ориентированные графы.

Количество вершин в графе обозначается V, а ребер — E. Если вершин сильно меньше, чем ребер — значит, в графе большое количество вершин не соединены ни с чем и их можно легко выкинуть. Здесь мы будем предполагать, что V = O(E).

Обход графа — это перебор его вершин в определенном порядке.

DFS

Depth First Search, или обход в глубину, является самым интуитивно понятным: в каждый момент времени мы перемещаемся из текущей вершины в любого из ранее непосещенных соседей (и помечаем его посещенным), а если таких нет — идем обратно. Если дополнительно записывать в массив для каждой вершины номер той, из которой мы в нее пришли — можно найти какой-нибудь путь из точки А в точку Б.

Сложность алгоритма

Для каждой вершины и каждого ребра мы выполняем константное количество действий, следовательно, сложность алгоритма — O(V + E) = O(E).

И, конечно же, код

Здесь и далее предполагается, что граф хранится в vector<vector> edges, где для каждой вершины записаны номера всех ее соседей, а также объявлен и изначально заполнен нулями массив пометок вершин vector mark.

void DFS(int v)
{
    if (mark[v] > 0) // если вершина уже посещена, делать тут больше нечего
    {
        return;
    }
    // Совершаем какие-нибудь полезные действия, например, можно вывести номер вершины на экран
    mark[v] = 1; // начали обработку
    for (int i = 0; i < (int)edges[v].size(); ++i) // запускаемся от всех соседей
    {
        DFS(edges[v][i]);
    }
    mark[v] = 2; // завершили обработку
}

BFS

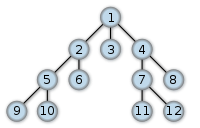DFS всем хорош, но с его помощью нельзя посчитать расстояние от одной вершины до другой — например, в графе выше вполне могло быть ребро от вершины 1 до вершины 5, которое мы не просмотрели (в момент его обработки вершина 5 уже помечена как обработанная).

Часто бывает полезно использовать обход графа, в котором вершины перебираются в порядке возрастания их расстояния от исходной. Но как именно можно это сделать?

Сначала рассмотрим начальную вершину, и добавим всех ее соседей в очередь. Потом для каждого из этих соседей рассмотрим уже всех его соседей и опять добавим их в очередь. Такой алгоритм обойдет все вершины в порядке, показанном на рисунке.

Сложность алгоритма

Для каждой вершины и каждого ребра мы выполняем константное количество действий, следовательно, сложность алгоритма — O(V + E) = O(E).

И, конечно же, код

void BFS(int v)
{
    // Инициализация
    queue<int> q;
    q.push(v);
    mark[v] = 1;
    // Работа самого алгоритма
    while (!q.empty())
    {
        // Берем вершину
        v = q.front();
        q.pop();
        // Смотрим всех ее соседей
        for (int i = 0; i < (int)edges[v].size(); ++i)
        {
            // И добавляем, если нужно
            if (mark[edges[v][i]] == 0)
            {
                markv[edges[v][i]] = mark[v] + 1;
                q.push(edges[v][i]);
            }
        }
    }
}

PS. Нерекурсивный DFS

Есть теорема о том, что любой рекурсивный алгоритм можно переписать в нерекурсивном виде. Вот код DFS:

void DFS(int v)
{
    stack<int> q;
    q.push(v);
    mark[v] = 1;
    while (!q.empty())
    {
        v = q.front();
        q.pop();
        for (int i = 0; i < (int)edges[v].size(); ++i)
        {
            if (mark[edges[v][i]] == 0)
            {
                markv[edges[v][i]] = mark[v] + 1;
                q.push(edges[v][i]);
            }
        }
    }
}

Автор: alexeykuzmin0

Источник