В предыдущем посте рассказывалось об обходе графа в глубину. Сегодня я бы хотел рассказать о не менее важном алгоритме теории графов — об обходе в ширину.
В прошлый раз мы уже научились искать какой-нибудь путь сквозь лабиринт. Всех желающих найти кратчайший путь прошу под кат.
Постановка задачи
Требуется найти путь от одной вершины графа до другой, причем путь должен быть минимальным по количеству ребер.
Описание алгоритма
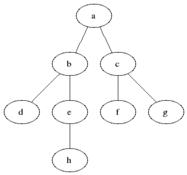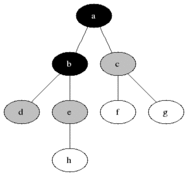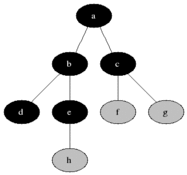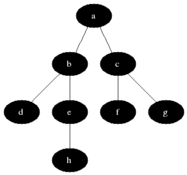Интуитивно хочется рассматривать вершины графа в порядке увеличения расстояния от исходной — так, как показано на рисунке.
Разделим все вершины на три множества:
- Полностью обработанные вершины (изначально множество пусто, на рисунке обозначено черным цветом)
- Вершины, до которых известно расстояние (изначально в множестве только одна вершина — начальная, на рисунке обозначено серым цветом)
- Вершины, про которые ничего не известно (изначально — все вершины, кроме начальной, на рисунке обозначено белым цветом)
Очевидно, что, как только все вершины черные, работа алгоритма завершена. Будем хранить все серые вершины в очереди и поддерживать следующее свойство: расстояния до всех серых вершин в том порядке, в котором они лежат в очереди, монотонно не убывают.
Достанем первую вершину из очереди (обозначим ее v). Для каждого из ее соседей w возможен один из двух вариантов:
- w — черная или серая вершина. В таком случае, мы не получаем никакой новой информации.
- w — белая вершина. Тогда расстояние до нее равно d(w) = d(v) + 1. И, поскольку мы узнали расстояние, w становится серой вершиной
Повторяем до тех пор, пока есть хотя бы одна серая вершина.
Реализация
Предполагается, что граф хранится в массиве vector<vector<int>> edges, причем edges[v] содержит номера всех вершин, к которым есть ребро от v. Также предполагается, что в глобальной переменной start хранится номер начальной вершины.
void BFS()
{
queue<int> q;
// Инициализация: есть информация про начальную вершину
q.push(start);
d[start] = 0;
// Главный цикл - пока есть серые вершины
while (!q.empty())
{
// Берем первую из них
int v = q.front();
q.pop();
// Пробегаемся по всем ее соседям
for (int i = 0; i < (int)edges[v].size(); ++i)
{
// Если сосед белый
if (mark[edges[v][i]] == 0)
{
// То вычисляем расстояние
d[edges[v][i]] = d[v] + 1;
// И он становится серым
mark[edges[v][i]] = 1;
q.push(edges[v][i]);
}
}
}
}
Почему это работает?
Рассмотрим любую вершину v, достижимую из начальной. Пусть p[0] = start, p[1], ..., p[k] = v — кратчайший путь из начальной вершины в вершину v. Тогда полученное в результате работы алгоритма значение d[v] = k.
Доказательство:
- d[v] ≤ k
- База: вершина p[0] = start посещается алгоритмом, причем d[p[0]] = 0
- Предположение: вершина p[i — 1] посещается алгоритмом, причем d[p[i]] ≤ i
- Шаг: при рассмотрении вершины p[i — 1] (а может, и раньше) будет рассмотрено ребро, ведущее в вершину p[i]. Таким образом, d[p[i]] ≤ i
- d[v] ≥ k
Предположим, что d[v] < k. Рассмотрим вершину v; ту вершину, при рассмотрении которой вершина v была покрашена в серый цвет (обозначим ее w); ту вершину, при рассмотрении которой вершина w была покрашена в серый цвет;…; начальную вершину start. Каждые две соседние вершины в этой последовательности соединены ребром по построению алгоритма. Таким образом, мы нашли путь из вершины start до вершины v длиной менее k — противоречие, следовательно, d[v] ≥ k
Сложность алгоритма
Для каждого ребра и каждой вершины алгоритм выполняет константное число действий, следовательно, временная сложность — O(V + E).
Максимальное число вершин, одновременно хранящихся в очереди — V, то есть, максимальный объем используемой памяти — O(V).
Вместо заключения
В этой статье мы нашли кратчайший путь через лабиринт с использованием одного из самых известных алгоритмов теории графов — BFS.
В следующий раз я постараюсь рассмотреть более сложную задачу на базе нашего любимого лабиринта и, на ее примере, рассказать алгоритм Дейкстры.
Автор: alexeykuzmin0
