Друзья, всем привет!
Пару месяцев назад, я уже начал рассказывать про методы помехоустойчивого кодирования. Первая статья была посвящена алгоритму Чейза. Она вот тут. Многих заинтересовало данное направление, поэтому я решил продолжить. На очереди весьма любопытный, перспективный, и что важно простой для понимания пороговый декодер. Давайте начнём!
Как работает
Пороговый декодер предоставляет чрезвычайно простое декодирование, основанное на принципе «голосования по большинству».
Кодер представляет собой регистр-очередь, заполненными битами вектора, который необходимо закодировать. Обработка начинается с нулевой ячейки. Для бита находящегося в нулевой ячейки вычисляются необходимые характеристики, а вышедший из очереди бит перемещается в конец очереди, в тринадцатую ячейку, и может быть использован для вычисления необходимых данных для бита, находящегося в нулевой ячейки. Механизм кодирования будет работать до тех пор, пока в нулевой ячейки не побывают все биты, исходного вектора.
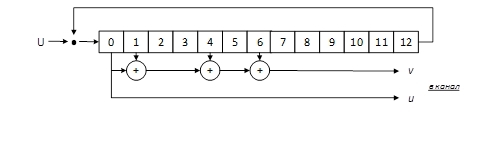
Можно сказать, что представленный кодер, задан с помощью «образующего полинома» g(x)=1+ x+x^4+x^6.
Таким образом, с процессе кодирования будет получены две части зашифрованного сообщения, которые в последствие будут объединены и переданы в канал, как единый вектор. Первая — информационная (u) будет содержать биты, исходного сообщения, переданные на прямую из нулевой ячейки регистра, кодируемого сообщения. Вторая – проверочная (v) будет содержать биты полученные путем сложения бит из ячеек регистра с индексами, соответствующим ненулевым степеням «образующего полинома» g(x).
Пример работы кодера
Пусть нам нужно зашифровать следующее сообщение: 0111011011011. Информационная ветвь (u) будет полностью соответствовать исходному сообщению, т.е. будет равна «1101101101110».
Проверочная ветвь (v) будет состоять из бит полученных за счёт сложения «по модулю два» бит, из 0-ой, 1-ой, 4-ой и 6-ой ячеек регистра.
Пример:
1. В регистре: 1 0 1 1 1 0 1 1 0 1 1 0 1
V = 1 ⊕ 0 ⊕ 1 ⊕ 1 = 1;
2. В регистре: 1 1 0 1 1 1 0 1 1 0 1 1 0
V = 1 ⊕ 1 ⊕ 1 ⊕ 0 = 1;
......
13. В регистре: 0 1 1 1 0 0 1 0 1 1 0 1 1
V = 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0;
После «круга» работы кодера, проверочная часть будет представлять собой вектор: «111000000010».
Следовательно, в канал будет отправлен вектор «10111011011011110000000010».
Стоит отметить что формат вектора [ u | v ] не является единственно верным. И может быть с легкостью заменен на любой другой формат, к примеру: [u1 | v1 | u2 | v2…un | vn].
Работа декодера
Рассмотрим работу порогового декодера. На первом шаге работы декодера, с помощью входящего в его состав кодера, вычисляются проверочные биты, для принятых из канала информационных битов ветви u, складывается «по модулю два» с принятыми проверочными битами из ветви v. В результате в синдромном регистре сформируется синдром, который указывает на наличие ошибок.
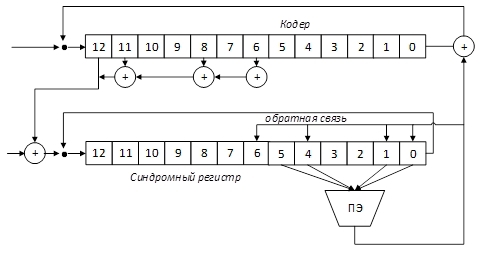
После заполнения синдромного регистра осуществляется декодирование информационного символа из 0-ой ячейки, для чего в пороговом элементе (ПЭ) осуществляется сравнение суммы элементов синдромного регистра, соответствующих декодируемому символу. В случае, если сумма окажется больше порога, выход ПЭ устанавливается равным 1, что приводит к изменению информационного символа и связанных с ним проверок. В противном случае ПЭ будет 0.
Рассмотренный декодер является декодером с обратной связью, так как исправление в информационном регистре ошибка за счёт обратной связи удаляется и из синдромного регистра.
Пусть в исходное сообщение «10111011011011110000000010» будет внесена ошибка «1011111101101 1110000000010».
Синдромный регистр будет содержать следующие значения: «00000011001010» (самый первый бит — ячейка «0» синдромного регистра на картинке)
1. В синдромном регистре: «0000011001010» → «0000011001010»
В пороге: 1, 1 < 2 → изменений нет. В результат идёт значение «1»;
2. В синдромном регистре: «0000110010100» → «0000110010100»
В пороге 1, 1 <2 → изменений нет. В результат идёт значение «1»;
......
6 В синдромном регистре: «1100101000000» → «0000000000000».
В пороге 4, 4 > 2 → изменение есть. В результат идёт значение «0», вносятся изменения в синдром;
В результате после декодирования мы получим сообщение «1 1 0 1 1 0 1 1 0 1 1 1 0». Ошибка была исправлена. И после инверсии позиций всех бит мы получим исходное сообщение «0 1 1 1 0 1 1 0 1 1 0 1 1».
Эпилог
Пороговый декодер является удачным сочетанием простоты реализации, эффективности и скорости работы. Его развитием является многопороговый декодер. Рассказать о котором попробую в ближайшее время.
Спасибо, всем кто прочёл. Буду рад конструктивным замечаниям/комментариям. Старался быть доходчивым :)
Автор: rznELVIS



