Введение
Всем доброго времени суток!
Уверен, что многие из вас уже интересовались методами разделения секретной визуальной информации. Если это так, то вы наверняка знакомы с работой Мони Наора и Ади Шамира, посвященной визуальной криптографии, а также с постом от 19 апреля 2013 года Схема разделения секретной визуальной информации . Я изучил предложенный в этой статье алгоритм и код функции, написанный на MATLAB, и пришел к выводу, что он написан не рационально: его можно записать значительно короче, а также повысить эффективность его работы. Как это сделать, я опишу ниже. Также рассмотрю как организовать.
Оптимизация кода
Недостатком приведенной функции является то, что в программе, многократно повторяется однотипный код, который увеличивает размер функции, усложняет ее выполнение, при том, что инструменты доступные в MATLAB, позволяют записать ее короче.
Я предлагаю оптимизировать код функции getShdwImg следующим образом:
function [S1,S2] =getShdwImgrac2x2(Img)
% получение теневых изображений S1 и S2 из исходного бинарного изображения (Img)
%
% получаем размер исходного изображения
[m,n] = size(Img);
% запасаемся памятью для каждого теневого изображения :)
S1= zeros(2*m,2*n);
S2= zeros(2*m,2*n);
r1=[1 0; 1 0];
r2=[0 1; 0 1];
r3=[0 0; 1 1];
r4=[1 1; 0 0];
r5=[1 0; 0 1];
r6=[0 1; 1 0];
r=cat(3, r1, r2, r3, r4, r5, r6);
% для каждого пикселя исходного изображения - действуем согласно Рис. 1
% Примечание:
for i=1:m-1
for j=1:n-1
k = randi(6);
if(Img(i,j)==1)
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k);
S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k);
else
if (mod(k,2) == 0)
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k);
S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1);
else
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k);
S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1);
end
end
end
end
Рассмотрим подробно, в чем состоят различия данного кода, по сравнению с исходным кодом:
- Объявим набор переменных r1-r6, размерностью 2х2, заполненных таким образом, чтобы получались комбинации состояний пикселя, приведенные на рисунке 1. Функция будет работать с 6 возможными комбинациями, в отличии от исходного кода.
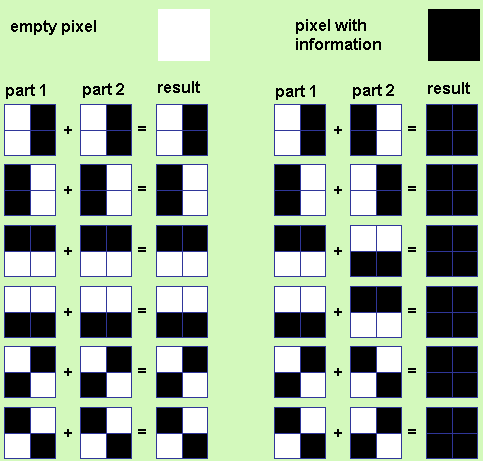
r1=[1 0; 1 0]; r2=[0 1; 0 1]; r3=[0 0; 1 1]; r4=[1 1; 0 0]; r5=[1 0; 0 1]; r6=[0 1; 1 0]; - Введенные переменные объединим в трехмерный массив с помощью команды cat(3, a, b, c…). Первый атрибут команды указывает на размерность массива, в который будут объединены массивы, перечисленные после первого атрибута.
r=cat(3, r1, r2, r3, r4, r5, r6); - Подключим оператор, генерирующий целочисленное значение переменной k случайным образом от 1 до 6.
k = randi(6); - Внутри условного оператора, в случае, когда выполняется условие, запишем переменные S1, S2. Ячейкам, которых будут присваиваться значения из переменной r. Значение будет зависеть от случайно сгенерированного числа k, так как обращаться будем к k слою r(:, :, k).
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); - В случае, если условие не выполнилось, тогда подключаю еще один условный оператор if. Его задача состоит в том, чтобы изменять индекс слоя массива r, который будет присваиваться переменным S1, S2. Так если переменная k – четная, то индексы будут присваиваться следующим образом:
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k-1);Иначе индекс слоя будет определяться по следующей формуле:
S1(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k); S2(2*i-1:2*i, 2*j-1:2*j)=r(:,:,k+1); - Изменять код Matlab-скрипта, демонстрирующего работу алгоритма разделения секретной визуальной информации, в данном случае нет необходимости.
close all % считываем исходное RGB-изображение и преобразуем его в бинарное biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); % пороговая фильтрация по Отсу (Otsu) biImg = im2bw(biImg,level); % выводим результат на экран figure(1) imshow(biImg); title(['Original binary image']); % получаем два теневых изображения [S1,S2] =getShdwImgrac2x2(biImg); % выводим их на экран figure(2) imshow(S1); title(['Shadow image S1']); % figure(3) imshow(S2); title(['Shadow image S2']); % выводим на экран результат их наложения друг на друга % различными способами figure(4) %imshow(and(S1,S2)); imshow(~xor(S1, S2)); % операция “~”(NOT) используется, чтобы получить черный текст на белом фоне, а не наоборот title(['Superimposed image']);

Исходное изображение

Исходное изображение, преобразованное в бинарное

Первое теневое изображение

Второе теневое изображение

Изображение, полученное путем совмещения двух теневых изображений, с применением логического оператора ~xor
А теперь предлагаю Вашему вниманию код функции для схемы разделения секрета Шамира (3,3) для бинарного изображения.
Разработка кода функции для схемы разделения секрета Шамира (3,3) для бинарного изображения
Данная функция предназначена для разделения изображения на три теневых. Исходное изображение можно будет восстановить, только совместив все три теневые изображения. В целом, ее код похож на код, изложенный выше, однако в ней имеется ряд существенных дополнений.
function [S1,S2,S3] =getShdwImgrac3x3opt(Img)
% Данная функция предназначена для получения теневых изображений
% S1, S2, S3 из исходного бинарного изображения (Img)
%
% получу размер исходного изображения
[m,n] = size(Img);
% создаю 3 матрицы в которы будут записываться теневые изображения )
S1= zeros(2*m,2*n);
S2= zeros(2*m,2*n);
S3= zeros(2*m,2*n);
% Набор матриц для замены пикселей исходного изображения
c01=[0 0 1 1; 0 1 0 1; 0 1 1 0];
c02=[1 0 0 1; 1 0 1 0; 0 0 1 1];
c03=[1 1 0 0; 0 1 0 1; 1 0 0 1];
c04=[0 1 1 0; 1 0 1 0; 1 1 0 0];
c0=cat(3, c01, c02, c03, c04);
c05=[1 1 0 0; 1 0 1 0; 1 0 0 1];
c06=[0 1 1 0; 0 1 0 1; 1 1 0 0];
c07=[0 0 1 1; 1 0 1 0; 0 1 1 0];
c08=[1 0 0 1; 0 1 0 1; 0 0 1 1];
c1=cat(3, c05, c06, c07, c08);
% для каждого пикселя исходного изображения создается 3 группы теневых
% пикселей
for i=1:m-1
for j=1:n-1
d=randi(4); % номер матрицы из множеств c
k = randperm(3); % выбор номера
if(Img(i,j)==1)
S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2);
S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2);
S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2);
else
S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2);
S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2);
S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2);
end
end
end
Рассмотрим подробнее отличия функции getShdwImgrac3x3opt от функции getShdwImgrac2x2.
- В переменные m, n записывается размер исходного изображения, после чего создается три нулевые матрицы с размерами 2*m, 2*n.
% получу размер исходного изображения [m,n] = size(Img); % создаю 3 матрицы в которы будут записываться теневые изображения ) S1= zeros(2*m,2*n); S2= zeros(2*m,2*n); S3= zeros(2*m,2*n); - На основе статьи Шамира разработал 4 массива из 4 столбцов и 3 строк для черного и белого пикселей соответственно. Каждые 4 массива объединяются в соответствующий трехмерный массив из 4 слоев.
% Набор матриц для замены пикселей исходного изображения c01=[0 0 1 1; 0 1 0 1; 0 1 1 0]; c02=[1 0 0 1; 1 0 1 0; 0 0 1 1]; c03=[1 1 0 0; 0 1 0 1; 1 0 0 1]; c04=[0 1 1 0; 1 0 1 0; 1 1 0 0]; c0=cat(3, c01, c02, c03, c04); c05=[1 1 0 0; 1 0 1 0; 1 0 0 1]; c06=[0 1 1 0; 0 1 0 1; 1 1 0 0]; c07=[0 0 1 1; 1 0 1 0; 0 1 1 0]; c08=[1 0 0 1; 0 1 0 1; 0 0 1 1]; c1=cat(3, c05, c06, c07, c08); - Теперь для каждого из пикселей исходного изображения создаются массивы из 4 ячеек по определенному алгоритму. Для перебора ячеек исходного изображения применяются два цикла, один переключает значения ячеек по вертикали, а второй по горизонтали.
Внутри цикла применяется целочисленный генератор псевдослучайных чисел, генерирующий номер слоя трехмерного массива, к которому мы обратимся. В другую переменную записываются всевозможные перестановки чисел от 1 до 3.for i=1:m-1 for j=1:n-1 d=randi(4); % номер матрицы из множеств c k = randperm(3); % выбор номера - Путем моделирование установил формулу, по которой необходимо обращаться к нужным ячейкам новых матриц. Каждым четырем ячейкам присваиваются соответствующие значения из матриц, составленных во 2 пункте алгоритма. Для того, чтобы правильно присвоить значение необходимо применить команду reshape(c0(k(1),1:4,d), 2, 2).
Данная команда позволяет трансформировать имеющуюся матрицу в матрицу заданного размера. Так первый параметр – обозначает название матрицы, которая будет трансформироваться, второй и третий параметры – размер матрицы, которую надо получить. В параметрах матрицы с0, переменная k(1) служит для выбора строки. При этом номер строки выбирается путем выполнения случайных перестановок, которые выполняются в пункте 3. Переменная d отвечает за выбор слоя трехмерной матрицы. Генерируется случайным образом в пункте 4.
В зависимости от цвета пикселя исходного изображения присваиваются значения либо из матрицы с0, либо из матрицы с1. Выбор необходимой матрицы осуществляется за счет условного оператора else.
После окончания условного оператора необходимо прописать закрывающие команды end.
if(Img(i,j)==1) S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(1),1:4,d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(2),1:4,d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c0(k(3),1:4,d), 2, 2); else S1(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(1,1:4, d), 2, 2); S2(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(2,1:4, d), 2, 2); S3(2*i-1:2*i, 2*j-1:2*j)=reshape(c1(3,1:4, d), 2, 2); end end end -
В этот раз незначительному изменению также подвергся Matlab-скрипт, вызывающий функцию getShdwImgrac3x3opt.
close all % считывание исходного RGB-изображение и преобразование его в бинарное biImg = imread('e_30.jpg'); biImg = rgb2gray(biImg); level = graythresh(biImg); % пороговая фильтрация по Отсу (Otsu) biImg = im2bw(biImg,level); % вывод на экран исходного изображения преобразованного % в бинарное figure(1) imshow(biImg); title(['Исходное изображение']); % получаем три теневых изображения из функции getShdwImgrac3x3opt [S1,S2,S3] =getShdwImgrac3x3opt(biImg); % вывод на экран первого теневого изображения figure(2) imshow(S1); title(['Первое теневое изображение ']); % вывод на экран второго теневого изображения figure(3) imshow(S2); title(['Второе теневое изображение ']); % вывод на экран третьего теневого изображения figure(4) imshow(S3); title(['Третье теневое изображение']); % выводим на экран результат их наложения друг на друга % различными способами figure(5) S12=xor(S1, S2); S=imshow(~xor(S12, S3));% операция “~”(NOT) используется, чтобы получить исходное изображение, % а не изображение с обратными цветами title(['Восстановленное бинарное изображение']);Главное отличие этого скритпа от его предыдущей версии состоит в том, что создается дополнительная переменная S12, в которую записывается матрица наложения изображений S1, S2. После этого в переменную S записывается результат наложения матриц S12, S3, который является окончательным результатом.
- Воспользуемся тем же исходным изображением и разобьем его на три теневые изображения
-



Теневые изображения - После выполнения наложения трех теневых изображений было получено исходное изображение:

Спасибо, всем, кто дочитал. Удачи!
Автор: Sany_KENT