
Всякий, знакомый с проблематикой кодирования информации, периодически сталкивался с идеями алгоритмов «суперсжатия» данных без потерь. Зачастую предлагается использование хеш-сумм, генераторов случайных чисел (зачем?), или просто различных комбинаций повторного сжатия данных при помощи архиваторов. После очередного бурного обсуждения, как правило, эксперты в очередной раз советуют первооткрывателям ознакомиться с азами теории информации. Особо упертым предлагают просто написать программу сжатия данных на один бит файла со случайными данными. После этого доселе бурно проходящее обсуждение «революционной технологии» постепенно сходит на нет.

Проблематика завлекает
Много лет назад, в ходе работы над программой анализа текстов, я также заинтересовался этой темой. В результате изучения фундаментальных основ современной теории информации, стало понятно, об какие камни спотыкались многочисленные первопроходцы, пытавшиеся с наскока решить эту проблему.
Первоосновы…

Все дело в структуре данных
Сжатие данных базируется на энтропийной кодировании, основанном на усреднении частот появления элементов в закодированной последовательности. То есть, только если символы некоторой последовательности данных встречаются в ней с различной вероятностью, тогда можно осуществить сокращение данных без потери информации. При этом, после такого сжатия в получившейся последовательности, частóты, с которыми появляются отдельные знаки, практически одинаковы (энтропия достигает своего максимального значения).

В глазах у Шеннона вселенская грусть — у сжатия данных есть свой предел
Согласно обратной теореме Шеннона об источнике кодирования, максимальная степень сжатия с помощью кодирования без потерь ограничивается энтропией источника. То есть, простыми словами — нельзя сжать данные больше, чем позволяет их энтропия, которая в свою очередь вычисляется по формуле:
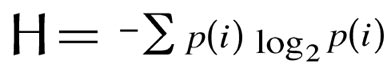
Из вышесказанного следует, что если логарифм вероятности появления того или иного элемента в данных, равен длине этого элемента, получить выигрыш от кодирования не удастся. При этом, после сколько-нибудь существенного сжатия данных без потерь, частóты распределений символов в получившейся последовательности стремятся к равномерному распределению, а стало быть, степень повторного сжатия этих данных стремится к нулю.
Не обязательно быть знакомым с основами теории информации, чтобы проверить верность этого утверждения. Достаточно взять любую программу для сжатия данных будь-то zip или rar, и попробовать повторно сжать уже заархивированный файл. Либо степень сжатия такого файла будет ничтожно мала, либо, что более всего вероятнее, повторное сжатие файла приведет к его увеличению (поскольку программа сжатия добавит к уже имеющемуся объему данных некоторую служебную информацию). То же самое произойдет и с другими программами для сжатия данных без потерь информации, даже с самыми эффективными.
Информационный взрыв
Как видим, существующие технологии кодирования информации бессильны перед существующим фундаментальным теоретическим пределом сжатия данных. При этом необходимо учитывать, что по одной оценке только в 2008 году было создано 487 миллиардов гигабайт цифровых данных. В 2011 году сгенерировано 1,8 трлн. гигабайт данных. А в 2012 создано уже в 5 раз больше цифровой информации, чем в 2008 году. При этом надо понимать, что речь в данном случае идет только о сохраненных данных — вся остальная информация, судя по всему, была для нас бесследно утеряна из-за банальной нехватки места для ее хранения. К настоящему моменту на планете Земля насчитывается более триллиона мобильных устройств. Только за один день создается более 2,5 млрд. гигабайт данных. То есть 500 млн. компакт-дисков данных ежедневно, которые можно выставить туда и обратно в два ряда от Солнца до планеты Плутон.
Масштаб проблемы...
В итоге, для хранения всей этой информации информационные компании постоянно увеличивают количество дата-центров. И этим гигантским сооружениям постепенно уже становится мало места на суше — данные переправляются в мировой океан, на плавучие дата-центры. И, увы, вся эта колоссальная масса электроники непрерывно потребляет огромное количество энергии и выделяет соответствующее ей количество тепла в атмосферу Земли.

Один из дата-центров. Матрица отдыхает...
Пытаемся обуздать хаос

Некоторые хаос почему-то представляют так...
Однако, при всей насущной потребности прорыва в технологиях сжатия данных, мы заходим в тупик фундаментальных основ теории информации. Поэтому, прекратив попытки пробить головой стену энтропийного предела сжатия данных, я решил более пристально изучить из чего, собственно, состоит эта стена. А состоит она из данных, энтропия которых стремится к максимальной, то есть, попросту говоря из хаоса.

Хотя он выглядит примерно так...
Именно хаос мы увидим, рассматривая данные сжатого файла. Возможно, это и не самый идеальный источник случайных данных, но в плоскости практического применения в сфере сжатия данных вполне подходит. Ведь достаточно найти хотя бы одну закономерность в этом хаосе, и ее будет можно использовать для дальнейшего сжатия данных.
Находим бреши в коде Вселенной

Казалось бы, нет более противоположных понятий, чем закономерность и хаос. Но, как оказалось, они тем не менее есть… На солнце есть пятна, а в хаосе есть свои закономерности.
Как уже было сказано ранее, если логарифм вероятности появления какого-либо элемента в данных не соответствует его длине, это дает возможность, согласно теореме о кодировании, сжать такие данные. Но существуют ли такие элементы в данных, энтропия которых максимальна?

Внимательно посмотри и найди 10 закономерностей (шутка)
Да, такие элементы имеют место быть в любых данных, энтропия которых близка к максимальной настолько, что их дальнейшее сжатие невозможно (в рамках существующих теоретических основ). В своих исследованиях я продвигался от более сложных структур данных к наиболее простым, так сказать, неким первоосновам или «атомам» хаоса.
Интересно? Следуй за белым кроликом просто за мной…
Что внутри кроличьей норы
Рассмотрим бинарный (двоичный) код сжатых данных, которые не поддаются дальнейшему сжатию никакой из существующих программ сжатия данных.
Возьмем, и последовательно слева направо заменяем все сочетания из трех знаков, из которых два знака одного вида находятся по бокам, а один знак другого вида находится посредине (проще говоря, сочетание «010» или «101») — активное кодовое слово (АКС) на новый знак, например, знак «2».
Например, во фрагменте «111000110101000010111» мы найдем два сочетания «101»: «1110001<101>010000<101>11» (знаки "<" и ">" приведены только для выделения АКС). После замены их на «2», фрагмент выглядит так: «11100012010000211». В результате такой замены, например, в 20 миллионах бит кода будет примерно 2001550 всех знаков «2».
Казалось бы, это означает, что данное сочетание появляется в коде с вероятностью 2001550:20000000=0.1000775, что дает ее двоичный логарифм в 3.320810439 бит. Однако это совсем не так. Тут не все так просто…
Допустим, мы убрали из кода все эти знаки «2». После этого мы опять обнаружим в нем эти же АКС “101”. Откуда они там взялись? А взялись они из сочетаний наподобие “110101,” которые мы заменили сначала на “1201”, а убрав “2” получили опять то же АКС “101”.
Например, после изъятия их из вышесказанного фрагмента, он выглядит так: «111000<101>000011». Сочетание «101» появилось после изъятия двойки из отрезка фрагмента «1201». Стало быть, в полученном фрагменте для восстановления первоначального состояния нужна информация только о расположении одного знака “2”, т. к. очевидно, что другая двойка обязательно должна будет расположена после первого знака в сочетании «101» — «1201» («1110001201000011»). Все двойки, которые располагались в подобных местах, можно не указывать в данных о расположении двоек. Значит для восстановления первоначальных данных, нам необходимы сведения только о расположении не 2001550, а 2001550-234200=1767350 двоек (где 234200 – это количество вновь появившихся АКС после того как мы убрали все 2001550 двоек из 20 000 000 бит кода с энтропией близкой к максимальной (ЭБМ)).
Кроме этого, необходимо учитывать, что двойка никогда не может располагаться после сочетания «10» (вот так — «102»), поскольку в результате предыдущих замен “101” на “2” отрезок «10101» превратился бы в «201», а не в «102» (т. к. замена идет слева направо), а затем (уже после изъятия двоек) останется «01». Поэтому все места после сочетаний «10» (после замены АКС на двойки) определяют как запретную зону (ЗЗ) для вставки новых двоек. Например, во фрагменте до изъятия двоек «11100012010000211» обнаружилось две таких ЗЗ — «1110*0012010*000211» (отмечены звездочками), что уменьшает число вариантов расположения АКС (двоек) — среди фрагмента«111H01201H00211» (где знаком «H» заменили «00»).
С учетом вышеизложенного, код расположения (КР) двоек для этого фрагмента можно записать в виде строки «00000000000200», и уже теперь убирать все двойки из фрагмента, который можно записать в виде строки “111H0101H0011”. Заменив знак H опять на «00», получаем «111000101000011».
Если проделать все эти замены в бинарном коде с ЭБМ, то вероятность появления двойки в КР получаем примерно 0.128-0.1285, что дает нам отрицательный двоичный логарифм в пределах 2.965-2.96, что, как мы видим, меньше битовой длины АКС. При этом уникальность ситуации заключается в том, что эта закономерность соблюдается вне зависимости от того, какого типа, структуры, вида файл был сжат. Главное, чтобы получившиеся в результате сжатия данные, имели ЭБМ, или проще говоря, их нельзя было сжать повторно.
Код хаоса взломан — что дальше?

Что делают хакеры, взломав код банка? Похищают деньги! Мы тоже будем похищать, но не деньги, а энтропию, внося во вселенский хаос упорядоченность и спасая вселенную от ее энтропийной (или тепловой) смерти.
Для 20 000 000 бит данных с ЭБМ в результате вышеуказанных манипуляций, мы получим не сжатый КР длиной примерно 13757030 бит (1767350 двоек среди 11989680 остальных знаков, которые мы обозначаем нулями). Код по формуле вычисления энтропии можно сжать до 7610719.618 бит. Логарифм (по основанию 2) отношения количества двоек к количеству всех знаков в этом примере равен 2.960509361 бит.
Что теперь делать? Записываем полученный КР 7610719.618 бит на бумажку в машинную память, а вместо него вставляем в оставшиеся знаки двойки так, чтобы вероятность их появления была равна 0.125 (логарифм вероятности соответственно 3 бита). Где взять этот код и что это нам даст?
Давайте посмотрим: нам нужно взять КР 1712811 знаков среди остальных 11989680 знаков (такой КР сжимается по формуле энтропии до 7448185.838 бит), что и даст нам требующуюся вероятность 0.125. Найти такой код проще простого — подобрать по нужному количеству один из знаков в восьмеричных данных с ЭБМ (3-битный восьмеричный алфавит), и перенести его КР в виде нового расположения двоек, которое будет соответствовать расположению изъятого знака из 8-ричных данных.
Каков выигрыш в сжатии данных от этих действий? Заменив одно количество АКС на другое, мы уменьшили общую длину сжимаемых данных на 54539 АКС (каждое длиной в три бита), т. е. уменьшили объем данных на 163617 бит. При этом, благодаря изъятию двоек среди остальных знаков, первоначальный код расположения 7610719.618 бит необходимо было сохранить для дальнейшего его восстановления. Зато вместо него размещением АКС в новом расположении, среди оставшихся, после удаления первоначального количества АКС, знаков, был записан другой код расположения АКС имеющий объем 7448185.838 бит (на который был уменьшен объем данных в восьмеричных данных с ЭБМ, которые мы превратили в 7-ричные, получив тот самый выигрыш примерно в 7448185 бит), что дало в разности увеличение кода на 7610719.618-7448185.838=162533.7798 бит. Однако общее уменьшение данных составило 162533.7798-163617=-1083.220189, т. е., округляя, 1083 бит.
«Бесконечное сжатие» для бесконечных данных

Конечно, можно возразить, что столь малая степень сжатия (20 миллионов бит мы сокращаем только на 1083 бит) является весьма небольшой. Однако нужно отметить, что в случае применения данного кодирования данных для их сжатия, такое сжатие можно повторить вновь и вновь.
В связи с этим необходимо разъяснить суть выражения «бесконечное сжатие». Естественно, что сжатие некоторых конечных данных возможно до определенного предела, который обусловлен конкретным видом кодирования, подобному вышеописанному. То есть, мы можем уплотнить какое угодно количество данных до определенного минимума (например, в вышеуказанном примере осуществления «бесконечного сжатия», возможно, например, уплотнить 20 гигабайт данных с ЭБМ до, например, 20 мегабайт, но, пока, отнюдь не до 200 байт). При этом, в дальнейшем, такой полученный несжимаемый минимум данных можно будет соединить с другими полученными минимумами данных и опять сжать уже объединенные таким образом данные вышеуказанным способом. Поэтому, именно для неограниченного объема данных существует возможность неограниченного уплотнения. Ограниченный объем данных уплотняется до некоторого определенного минимального предела.
«Прочитал, допустим, это правда. В чем подвох?»
Да, действительно, подвох, или скорее нюанс, действительно имеется. Суть этого нюанса заключается в том, что на этапе сжатия данных КР АКС в арифметическом кодировании необходимо применять более длинную арифметику, чем имеется в известных мне программах сжатия данных. Обычно при арифметическом кодировании более длинная арифметика не дает ничего в практическом плане, давая выигрыш в сжатии в ничтожно малые доли процентов, весьма существенно замедляя при этом время сжатия. Однако, в данном случае, эти ничтожно малые доли процентов являются критичными в ходе каждого цикла сжатия.

Пока Гарольд под прикрытием сеет доброе вечное, молодой гений пишет на листочке код программы суперсжатия… (Person of Interest S02E11 (С)
Так что, обращаюсь ко всем толковым программистам с предложением написать модуль арифметического кодирования с более длинной арифметикой на более быстром языке программирования, нежели BASIC. Чуть позже выложу файл с КР АКС, чтобы предметно было видно, с чем придется иметь дело при сжатии.

Стартап это еще тот адреналин. Ведь на самом деле всё только начинается...(Silicon Valley (С)
Все авторские права и прочая интеллектуальная собственность принадлежат их законным правообладателям (в том числе мне ;). Все изображения приведены только в качестве учебных иллюстраций и принадлежат их законным правообладателям. Patents pending.
• Shannon C. E. Communication in the presence of noise // Proc. Institute of Radio Engineers. — Jan. 1949. — Т. 37. — № 1. — С. 10—21.
• Шеннон К. Работы по теории информации и кибернетике. — М.: Изд-во иностранной литературы, 1963. — 830 с.
• Малинецкий Г. Г. Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. 3-е изд. М.: УРСС, 2001.
• Малинецкий Г. Г., Потапов А. Б., Подлазов А. В. Нелинейная динамика: подходы, результаты, надежды. М.: УРСС, 2006.
Автор: ILIN-AIC






0.005% сжатия за 1 проход это бред!
Нужно сделать 13862 прохода, при таком раскладе, чтобы сжать файл в двое… а это прежде всего время, а время это деньги за электричество и за занятое оборудование в этом деле.
Признаться, я и сам ищу разные методы супер сжатия, но этот мне кажется малоперспективным. Хотя если выйдут в продажу квантовые компьютеры для обычных пользователей и появиться дешевый источник энергии, то возможно данный алгоритм будет пользоваться спросом)
гораздо более эффективный путь очень сильного сжатия — https://pkprovincia.000webhostapp.com/2019/03/математическое-сжатие-или-новое-каче