Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.
В русскоязычных источниках очень мало литературы на этот счет. А цельное представление вообще получить практически нереально. Благо, моим научным руководителем оказался как раз знаток энтропийного анализа и автор свеженькой монографии [1], где все расписано «от и до». Счастью предела не было, и я решила попробовать донести мысли на этот счет до более широкой аудитории, так что пару выдержек возьму из монографии и дополню своими исследованиями. Может, кому и пригодится.
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона
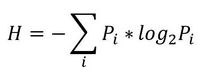 , где Pi это вероятность наступления i-го исхода.
, где Pi это вероятность наступления i-го исхода.
То есть в этом случае энтропия напрямую связана с «неожиданностью» возникновения события. А отсюда вытекает и его информативность — чем событин более предсказуемо, тем оно менее информативно. Значит и его энтропия будет ниже. Хотя открытым остается вопрос о соотношениях между свойствами информации, свойствами энтропии и свойствами различных ее оценок. Как раз с оценками мы и имеем дело в большинстве случаев. Все, что поддается исследованию — это информативность различных индексов энтропии относительно контролируемых изменений свойств процессов, т.е. по существу, их полезность для решения конкретных прикладных задач.
Энтропия сигнала, описываемого некоторым образом (т.е. детерминированного) стремится к нулю. Для случайных процессов энтропия возрастает тем больше, чем выше уровень «непредсказуемости». Возможно, именно из такой связки трактовок энтропии вероятность->непредсказуемость->информативность и вытекает понятие «хаотичности», хотя оно достаточно неконкретно и расплывчато (что не мешает его популярности). Встречается еще отождествление энтропии и сложности процесса. Но это снова не одно и то же.
Едем дальше.
Энтропия бывает разная черная белая красная:
- термодинамическая
- алгоритмическая
- информационная
- дифференциальная
- топологическая
Все они различаются с одной стороны, и имеют общую основу с другой. Конечно, каждый вид применяется для решения определенных задач. И, к сожалению, даже в серьезных работах встречаются ошибки в интерпретации результатов расчета. А все связано с тем, что на практике в 90% случаев мы имеем дело с дискретным представлением сигнала непрерывной природы, что существенно влияет на оценку энтропии (на деле там в формулке появляется поправочный коэффициент, который обычно игнорируют).
Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).
Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.
Разбив x на реализации по 100 отсчетов можно построить эмпирическую плотность распределения и по ней вычислить значение энтропии Шеннона. Получим значения, «разнесенные» по уровням (рисунок 1.6).
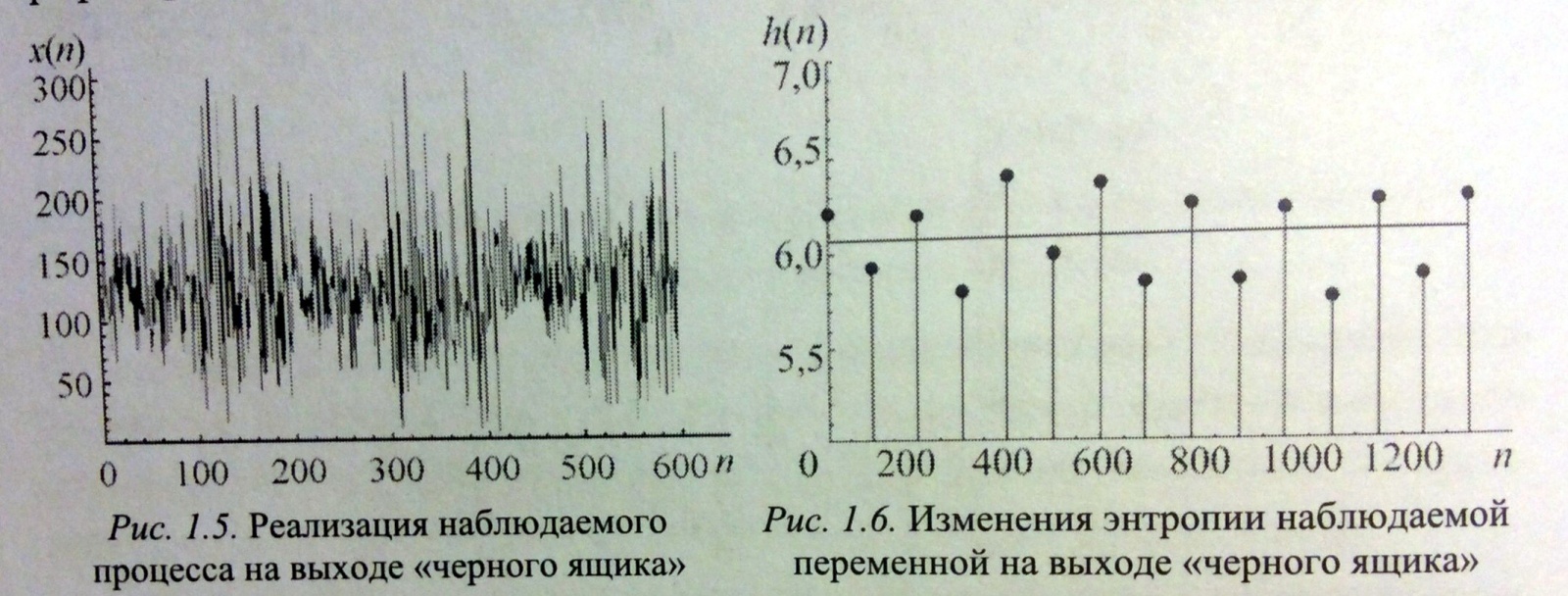
Как можно видеть, переходы между состояниями явно наблюдаются. Но что делать в случае, если время переходов нам не известно? Как оказалось, вычисление скользящим окном может помочь и энтропия так же «разносится» на уровни.В реальном исследовании мы использовали такой эффект для анализа ЭЭГ сигнала (разноцветные картинки про него будут дальше).
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.
Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).
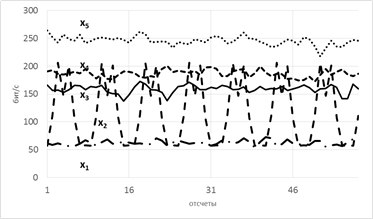
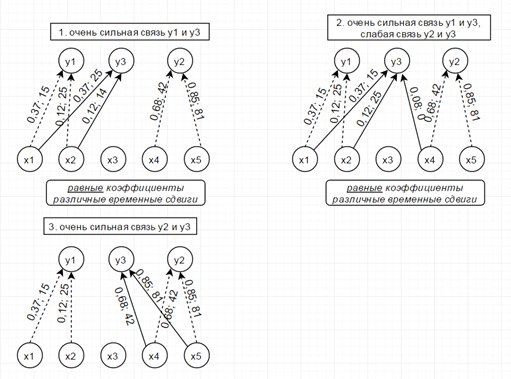
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!
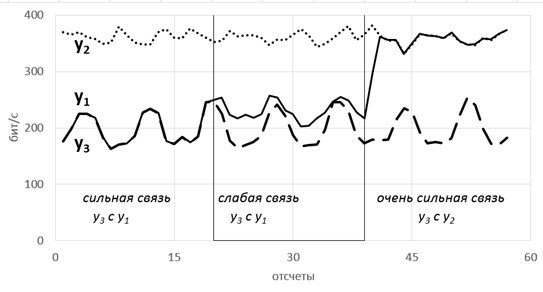
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.
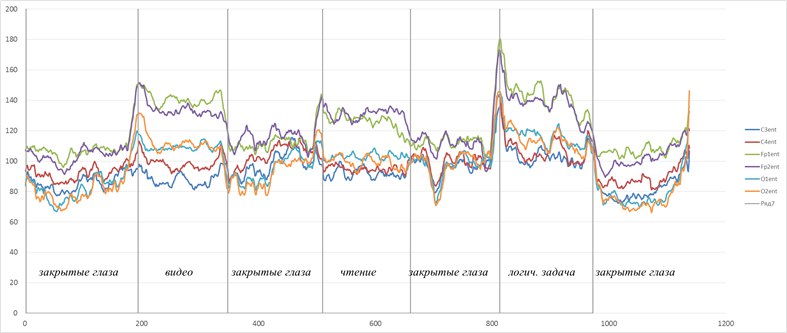
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).
Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.
P.S. При наличии интереса, могу немного подробней поговорить в следующий раз об алгоритмах расчета энтропии и почему энтропию Шеннона сейчас почти не используют.
Литература
1. Цветков О.В. Энтропийный анализ данных в физике, биологии и технике. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2015. 202 с.
2.Abásolo D.,Hornero R., Espino P. Entropy analysis of the EEG background activity in Alzheimer’s disease patients // Physiological Measure-ment. 2006. Vol. 27(3). P. 241 – 253. epubs.surrey.ac.uk/39603/6/Abasolo_et_al_PhysiolMeas_final_version_2006.pdf
3. 28. Bruce Eugene N, Bruce Margaret C, Vennelaganti S. Sample entropy tracks changes in EEG power spectrum with sleep state and aging // Journal of Clinical Neurophysiology. 2009. Vol. 26(4). P. 257 – 266. www.ncbi.nlm.nih.gov/pubmed/19590434
4. Энтропийный анализ как метод безгипотезного поиска реальных (гомогенных) социальных групп (О. И. Шкаратан, Г. А. Ястребов) www.sociologos.ru/metody_i_tehnologii/Razdel_Analiz_dannyh/Statisticheskij_analiz/Entropijnyj_analiz_kak_metod_bezgipoteznogo_poiska_realnyh_gomogennyh_socialnyh
5. Энтропийные и другие системные закономерности: Вопросы управления сложными системами. Прангишвили И.В. apolov-oleg.narod.ru/olderfiles/1/Prangishvili_I.V_JEntropiinye_i_dr-88665.pdf
Автор: YuliyaCl