Всем привет! Хочу поделиться небольшой историей допиливания HeatonResearchNeural — библиотеки разнообразных нейросетей. Сразу оговорюсь, что работаю аналитиком, а честным программистом перестал быть лет 10 назад.
Однако у меня есть собственный проект на C#, который развиваю в свободное время. Чтобы не заморачиваться написанием велосипеда когда-то скачал HeatonResearchNeural прикрутил скотчем и спокойно гонял тесты, дорабатывал логику своего кода и т.д. Для максимального ускорения заложил в архитектуру решения параллелизацию выполнения расчетов и глядя на загрузку CPU по 80-90% по телу разливалось приятное хозяйское тепло — все пашут, все при деле!
С другой стороны, объемы у меня большие, ждать приходилось долго, пока она отработает. Подумывал даже о покупке второго сервера, пока меня вдруг не посетила мысль заглянуть под капот этого самого велосипеда при помощи профилировщика. Причем возникла не сама по себе, а под впечатлением данной статьи уважаемого хабробщества.
Изначально в своем коде я был уверен. Понятно, что нейросеть эта такая вещь, которая должна летать, иначе не вытянет серьезных тем. Однако, прямо как после чтения медицинского справочника обнаруживаешь у себя большинство признаков самых чудовищных заболеваний, решил все-таки провериться пройтись по коду профилировщиком.
Когда профилирование указало на библиотечные функции, в душе затрепетало хладнокровное волнение. Понятно, что разработчики такой хорошей библиотеки подумали про скорость, верно? Или миром все-таки правит не тайная ложа, а явная лажа? Чтобы ответить на этот вопрос давайте рассмотрим внимательнее результат прогона 100 циклов моей программы, почти целиком состоящей из работы нейросетей:
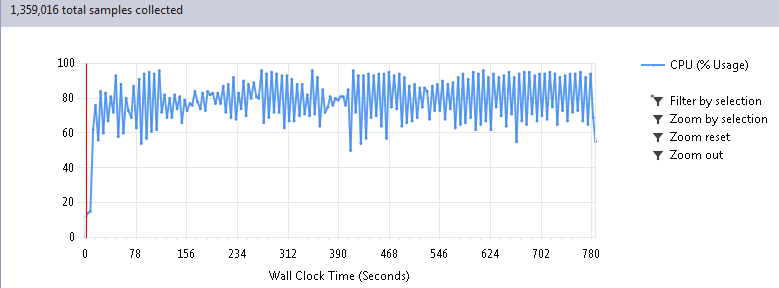
Проваливаемся в Call Tree отчета и находим самые тяжелые функции:
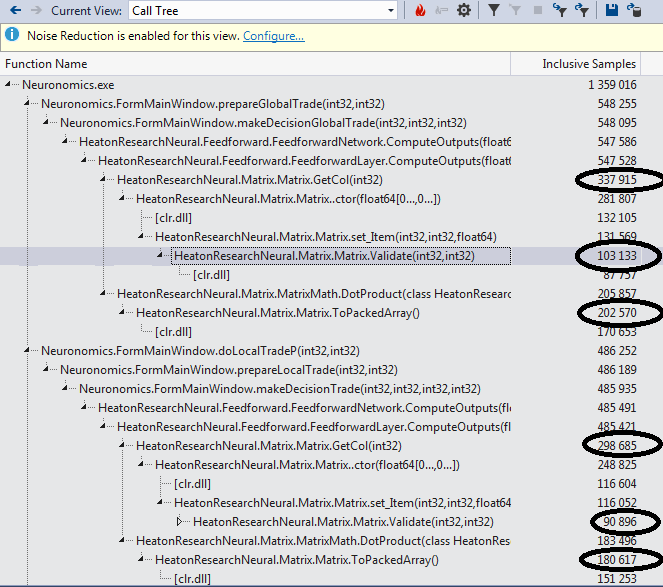
Идем к ним и видим воистину душераздирающее зрелище. Если вы не совершенно уверены в своей психике, возможно имеет смысл отвернуться и не видеть, как функция GetCol занимается богопротивным извлечением вектора из матрицы:
public Matrix GetCol(int col)
{
if (col > this.Cols)
{
throw new MatrixError("Can't get column #" + col
+ " because it does not exist.");
}
double[,] newMatrix = new double[this.Rows, 1];
for (int row = 0; row < this.Rows; row++)
{
newMatrix[row, 0] = this.matrix[row, col];
}
return new Matrix(newMatrix);
}
Лишь для передачи в DotProduct:
for (i = 0; i < this.next.NeuronCount; i++)
{
Matrix.Matrix col = this.matrix.GetCol(i);
double sum = MatrixMath.DotProduct(col, inputMatrix);
this.next.SetFire(i, this.activationFunction.ActivationFunction(sum));
}
Лишаем этого паразита питательных и полных витаминами гигагерц двумя точными ударами прямого слэша и передаем в DotProduct сразу всю матрицу вместе с нужным номером колонки:
//Matrix.Matrix col = this.matrix.GetCol(i);
double sum = MatrixMath.DotProduct(this.matrix, i, inputMatrix);
А уже внутри вместо изящного кружева:
public static double DotProduct(Matrix a, Matrix b)
{
if (!a.IsVector() || !b.IsVector())
{
throw new MatrixError(
"To take the dot product, both matrixes must be vectors.");
}
Double[] aArray = a.ToPackedArray();
Double[] bArray = b.ToPackedArray();
if (aArray.Length != bArray.Length)
{
throw new MatrixError(
"To take the dot product, both matrixes must be of the same length.");
}
double result = 0;
int length = aArray.Length;
for (int i = 0; i < length; i++)
{
result += aArray[i] * bArray[i];
}
return result;
Лепим простой, как топор, быдлокод:
public static double DotProduct(Matrix a, int i, Matrix b)
{
double result = 0;
if (!b.IsVector())
{
throw new MatrixError(
"To take the dot product, both matrixes must be vectors.");
}
if (a.Rows != b.Cols || b.Rows != 1)
{
throw new MatrixError(
"To take the dot product, both matrixes must be of the same length.");
}
int rows = a.Rows; // Так будет гораздо быстрее, чем если указать a.Rows прямо в условии цикла
for (int r = 0; r < rows; r++)
{
result += a[r, i] * b[0, r];
}
return result;
Валидаторы на выход за пределы массива тоже имеет смысл закомментировать, все равно размеры задаются статически при компиляции и тут сложно накосячить, а времени на них убивается столько же, сколько японцев с небоскребов при ослаблении йены на 5%.
public double this[int row, int col]
{
get
{
//Validate(row, col);
return this.matrix[row, col];
}
set
{
//Validate(row, col);
if (double.IsInfinity(value) || double.IsNaN(value))
{
throw new MatrixError("Trying to assign invalud number to matrix: "
+ value);
}
this.matrix[row, col] = value;
}
}
Итак, волнительный момент, запускаем опять 100 циклов программы. Когда я увидел эффект от этих нехитрых действий, мне чуть не поплохело от радости. Такое странное чувство, как будто тебе вот так взяли и подарили 30 серваков (которые, оказывается, стояли у тебя же в шкафу, но ты просто не догадывался туда заглянуть):
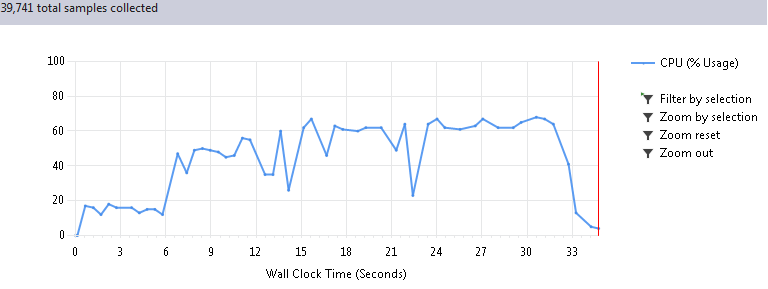
Первые 6 секунд на графике это подготовка данных, поэтому реальное время работы сократилось с 780 до 26 секунд, при абсолютно одинаковом результате, естественно. Таким образом, ускорение получилось в 30 раз!
Таким образом, практика еще показывает, что законы Мерфи вкалывают также стабильно, как афроамериканцы сидят на велфере и если что-то может пойти не так, то можно не сомневаться, так оно и случится. Также стоит отметить, что возможно некоторые виды сетей не будут работать на таком коде, это стоит протестить и учесть при необходимости. Всем спасибо за внимание, надеюсь это кому-нибудь хоть как-то поможет в успешной борьбе с неудержимо разрастающейся энтропией вселенной и кода.
Автор: pustota_2009