Предыстория
Чтобы летом держать в тонусе я скачал себе сборник головоломок. По началу задания были довольно простыми и не особо требовательными к проявлению логики, но по ходу игры чувствовалось нарастающее усложнение.
В какой-то момент я застрял на головоломке под названием «Китайские шашки». Редкие потуги решить её своими силами не приносили особых плодов на протяжение долгого времени и в итоге я отложил свои муки с решением до лучших времен.
Закончилась зимняя сессия, а до начала учебы еще пара недель — чем не «лучшие времена»? Я заглянул в интернет, дабы проверить есть ли у данной головоломки вообще хоть какое-нибудь решение, и первые же результаты поискового запроса убедили меня в том, что оно действительно существует.
Я не стал подглядывать в прохождение, мне хотелось дойти до него своими силами — или самому решить, или написать программу, которая найдет мне это решение. Однако напрямую применить силу
— «Ну всё, пусть эта головоломка поговорит с моим многоядерным другом!» — пронеслось у меня в голове, и я сел за написание брутфорса.
Постановка задачи
Поле — 33 ячейки, 32 из которых заняты фишками. Цель — съесть максимально возможное количество фишек(должна остаться лишь одна). Есть можно только по вертикали и горизонтали таким образом:

Пример хода
Первая попытка решения
Первый брутфорс был написан без учета теории за пол-часа, его идея заключалась в рекурсивном спуске по дереву возможных ходов, с рандомным выбором каждого последующего хода.
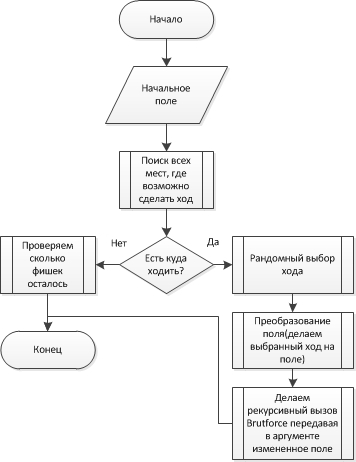
Псевдо блок-схема первой версии
И всё это чудо вертелось в цикле. В первые 15 секунд он даже смог найти ход решения приводящий к 3 остающимся фишкам на поле, а в последующую минуту и к 2! Но радость была не долгой, ибо рандом, пусть даже псевдо, трудно предсказуем — за ночь работы он не смог более приблизиться к решению. Становилось очевидна потребность рассмотрения вопроса с теоретической точки зрения.
Немного теории
Если действующее игровое поле вытянуть в строку, то получится 33 разрядное двоичное число, где 1 соответствует ячейке с фишкой, а 0 пустой ячейке. Соответственно всего состояний у поля может быть не больше 2^33 — 2, так как по правилам поле не может стать полностью пустым(всегда остается хотя бы одна фишка), или полностью заполненным фишками(их дается 32 изначально и больше уже стать не может).
Это можно интерпретировать как то, что ходов у нас всего не более 8 589 934 590, что вполне перебираемо на домашнем компьютере. То есть нужно просто написать честный полный перебор.
Вторая попытка решения
Избавившись от рандомной составляющей алгоритм брутфорса принял следующий вид:
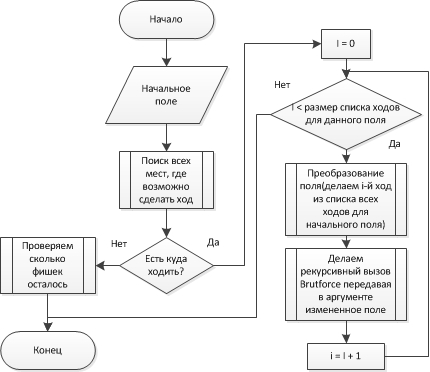
Псевдо блок-схема второй версии
Этот брутфорс написанный на C++ на всех известных мне оптимизациях в релиз-версии работал довольно резво, перебирая чуть ли не 200 000 ходов в секунду, а значит для полного перебора понадобилось бы (2^33 — 2) / (2 * 10^5) ≈ 12 часов. Но так как четыре варианта первого хода очевидно ведут к лишним повторениям, то мы делаем первый ход за программу, таким образом на 3/4 уменьшая количество ходов которые требуется перебрать(а значит и время работы). Программа занимала в оперативной памяти 2.6 МБ и довольно быстро перебрала 2 * 10^7 ходов и все бы ничего, но ответа до сих пор не было.
Самое веселье же было в том, что на этих двух миллиардах программа показывала что перебирает подветвь дерева всех возможных ходов которая образуется после 12 хода! Что-то тут не так, либо ошибка в брутфорсе, либо существуют такие различные ходы, которые приводят поле к одному состоянию, причем этих пересечений должно быть достаточно много.
Мои опасения подтвердились простейшей проверкой — разные ходы действительно могли приводить поле в одно и то же состояние.
Третья попытка решения
Значит нужно сохранять рассчитанные поля и при обнаружение повтора сразу сообщать, что их считать не нужно.
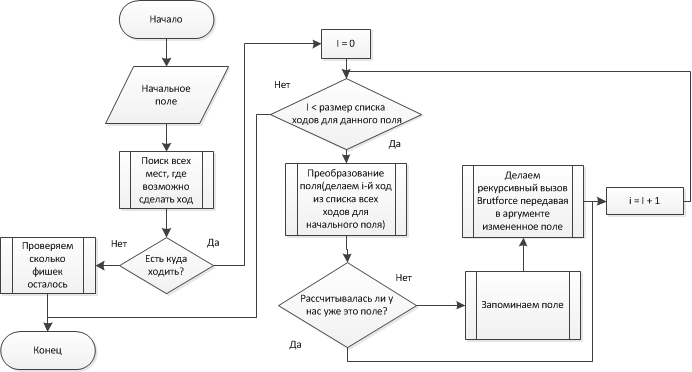
Псевдо блок-схема третьей версии с запоминанием рассчитанных полей
Только вот это дело оказалось весьма накладным, если хранить просчитанные поля в оперативной памяти, то получается в идеальном случае что нам потребуется 33 бита на одно поле, а их даже с учетом сделанного первого хода (2^33 — 2) / 4, то есть памяти понадобится на хранение всех просчитанных полей ((2^33 — 2) / 4) * 33) / (8 * 2^20) ≈ 8.5 ГБ, а у меня всего 4, из которых я могу дать программе лишь 2. Что же делать? Особенно если учесть, что 33 бита это теоретический минимум требуемый на игровое поле, а на практике их ведь постоянно нужно сравнивать, да и не как-то там, а побитово! Можно было поискать системные функции для побитового сравнения двух участков памяти, или попробовать сделать это ассемблерными вставками. Но все равно нужно ведь будет хранить еще и указатели на эти поля, то есть в 33 бита игрового поля + 4 байта указатель(на моей машине) на них + выравнивание структур в памяти — ну никак не уложиться даже с оперативкой в 16 ГБ. Можно было бы попробовать сделать хранение на диске, но тогда скорость перебора упала бы на непозволительный уровень…
В итоге было решено опробовать злосчастный std::vector bool для хранения рассчитанных полей и молиться о том, чтобы ход решения был найден до того, как иссякнет память.
Новый брутфорс перебирал около 7000 ходов в секунду, но этого оказалось вполне достаточно — по счастливому стечению обстоятельств я выловил аж 4 решения до того как выскочила плашка «Memory out». Память иссякла когда он перебрал пять миллионов ходов и находился при этом на подветви дерева всех возможных ходов которая образуется после 5 хода от начала игры.
Заключение
Вроде головоломка и решена своими силами, но недосказанность осталась. Решение вполне могло и не находится в перебранном мной диапазоне, тогда бы пришлось думать дольше, и возможно уже совсем в ином направление.
PS Перед публикацией нашел на хабре пост Применяем на практике знания, полученные на курсе MIT 6.00x (edx.org) часть которого повествовала о решение этой же задачи, но справедливости ради замечу что мы с автором того поста пошли разными путями.
PPS Возможно наличие ошибок и неточностей, буду признателен за поправки и советы.
#include <iostream>
#include <fstream>
#include <list>
#include <string>
#include <set>
#include <vector>
namespace China_Checkers
{
// Size of the game field
unsigned x, y;
// Class of game field for storage
class Field
{
static const unsigned size;
std::vector<bool> *field;
bool is_copy;
public:
Field(bool** f)
{
field = new std::vector<bool>(size);
// Transforming game field as matrix to vector
for (unsigned i = 0; i < x; ++i)
{
for (unsigned j = 0; j < y; ++j)
{
if ((i > 1 && i < 5) && (j < 2 || j > 4))
field->push_back(f[i][j]);
else if (j > 1 && j < 5)
field->push_back(f[i][j]);
}
}
}
Field(Field& f)
{
f.is_copy = true;
field = f.field;
}
Field &operator=(Field& f)
{
f.is_copy = true;
field = f.field;
}
friend bool operator==(const Field& m1, const Field& m2)
{
if (m1.field == m2.field) return true;
if ((*m1.field) != (*m2.field)) return false;
return true;
}
friend bool operator<(const Field& m1, const Field& m2)
{
if ((*m1.field) < (*m2.field)) return true;
return false;
}
~Field()
{
if (is_copy)
return;
delete field;
}
};
const unsigned Field::size = 33;
class China_Checkers_Hack
{
typedef bool** field ; // Type of a game field
typedef std::pair<unsigned, unsigned> position; // Pair of x, y
typedef std::pair<position, position> move ; // Type for a move (start position, end position)
typedef std::pair<field, std::list<move*>*> step ; // Type for description one step of the bruteforce
int win_condition; // Condition scoring
std::list<field> path_to_win ; // Path to win
std::set<Field> fld_buf ; // We checked these fields
// To output a field in a stream
friend std::ostream &operator<<(std::ostream &out, const field fld)
{
if (fld == nullptr)
{
std::cout << "Attempt to output nullptr field" << std::endl;
system("pause");
return out;
}
for (unsigned j = 0; j < x ; ++j)
{
for (unsigned i = 0; i < y; ++i)
{
if (((i < 2) || (i > 4)) && ((j < 2) || (j > 4)))
out << '*' << ' ';
else
out << fld[i][j] << ' ';
}
out << 'n' << std::flush;
}
return out;
}
// To display a some message
void message(const std::string msg = "")
{
std::cout << "Message: " << msg << std::endl;
system("pause");
}
// Returns a pointer to a memory was allocated for a field, or nullptr in error case
field alloc_mem_for_field()
{
field fld = nullptr;
try
{
fld = new bool*[x];
for (unsigned i = 0; i < x; ++i)
{
fld[i] = new bool[y];
}
}
catch(std::bad_alloc)
{
fld = nullptr;
message("Memory out in alloc_mem_for_field()");
}
return fld;
}
// Copy a field and returns a reference on it, or nullptr in error case
field copy_field(field fld_dest, const field fld_source)
{
if (fld_dest == nullptr)
{
if ((fld_dest = alloc_mem_for_field()) != nullptr)
{
for (unsigned i = 0; i < x; ++i)
{
for (unsigned j = 0; j < y; ++j)
{
fld_dest[i][j] = fld_source[i][j];
}
}
}
}
else
{
for (unsigned i = 0; i < x; ++i)
{
for (unsigned j = 0; j < y; ++j)
{
fld_dest[i][j] = fld_source[i][j];
}
}
}
return fld_dest;
}
// First initialize of a field
void init_field(field &fld)
{
for (unsigned i = 0; i < x; ++i)
{
for (unsigned j = 0; j < y; ++j)
{
if (
(((i == 0) || (i == 1)) || ((i == (x - 1)) || (i == (x - 2))))
&&
(((j == 0) || (j == 1)) || ((j == (y - 1)) || (j == (y - 2))))
)
fld[i][j] = (bool)2; // Not used
else
fld[i][j] = 1;
}
}
// Make the first move to reduce space of moves on 3/4
fld[(x / 2)][(y / 2)] = 1;
fld[(x / 2)][(y / 2 - 1)] = 0;
fld[(x / 2)][(y / 2) - 2] = 0;
}
// Returns num of chips on field
int IsWin(const field &fld)
{
int k = 0;
for (unsigned i = 0; i < x; ++i)
{
for (unsigned j = 0; j < y; ++j)
{
if (
(i < 2 || i > 4)
&&
(j < 2 || j > 4)
)
continue;
if (fld[i][j] == 1)
++k;
}
}
return k;
}
// Free alloc memory
void free_mem_from_field(field &fld)
{
if (fld == nullptr)
{
message("Attempt to delete nullptr in free_mem_from_field()");
return;
}
for (unsigned i = 0; i < y; ++i)
{
delete[] fld[i];
}
delete[] fld;
fld = nullptr;
}
// Returns true if a cell is empty
bool IsCell(const field &fld, const int lx, const int ly)
{
if (
(lx > 0 && ly > 0)
&&
(lx < (int)x && ly < (int)y)
&&
(!((lx < 2 || lx > 4) && (ly < 2 || ly > 4)))
)
{
if (fld[(unsigned)lx][(unsigned)ly] == 0) return true;
}
return false;
}
// Returns true if a cell has a chip
bool IsChip(const field &fld, const int lx, const int ly)
{
if (
(lx > 0 && ly > 0)
&&
(lx < (int)x && ly < (int)y)
&&
(!((lx < 2 || lx > 4) && (ly < 2 || ly > 4)))
)
{
if (fld[(unsigned)lx][(unsigned)ly] == 1) return true;
}
return false;
}
// Returns a pointer on a list of all moves for the current field
// or nullptr if moves doesn't exist
std::list<move*> *get_all_moves(const field &fld)
{
std::list<move*> *buf = nullptr;
try
{
buf = new std::list<move*>;
move* m = nullptr;
for (int i = 0; (unsigned)i < x; ++i)
{
for (int j = 0; (unsigned)j < y; ++j)
{
if ((fld[i][j] == 1) && (!(((i < 2) || (i > 4)) && ((j < 2) || (j > 4)))))
{
if (IsCell(fld, i + 2, j))
{
if (IsChip(fld, i + 1, j))
{
m = new move();
m->first.first = i;
m->first.second = j;
m->second.first = i + 2;
m->second.second = j;
buf->push_back(m);
}
}
if (IsCell(fld, i - 2, j))
{
if (IsChip(fld, i - 1, j))
{
m = new move();
m->first.first = i;
m->first.second = j;
m->second.first = i - 2;
m->second.second = j;
buf->push_back(m);
}
}
if (IsCell(fld, i, j + 2))
{
if (IsChip(fld, i, j + 1))
{
m = new move();
m->first.first = i;
m->first.second = j;
m->second.first = i;
m->second.second = j + 2;
buf->push_back(m);
}
}
if (IsCell(fld, i, j - 2))
{
if (IsChip(fld, i, j - 1))
{
m = new move();
m->first.first = i;
m->first.second = j;
m->second.first = i;
m->second.second = j - 2;
buf->push_back(m);
}
}
}
}
}
if (buf->size() == 0)
{
delete buf;
buf = nullptr;
}
}
catch (std::bad_alloc)
{
delete buf;
buf = nullptr;
message("Memory out in get_all_moves()");
}
return buf;
}//*/
// To make a move
field make_move(field fld, const move &mv)
{
if (fld == nullptr)
{
message("Attempt to move on empty field in make_move()");
return fld;
}
if (mv.first.first != mv.second.first)
{
if (mv.first.first < mv.second.first)
{
fld[mv.first.first + 1][mv.second.second] = 0;
}
else
fld[mv.first.first - 1][mv.second.second] = 0;
}
else if (mv.first.second != mv.second.second)
{
if (mv.first.second < mv.second.second)
{
fld[mv.first.first][mv.first.second + 1] = 0;
}
else
fld[mv.first.first][mv.first.second - 1] = 0;
}
else
{
message("Move is incorrect, error in get_all_moves()");
return fld;
}
fld[mv.first.first][mv.first.second] = 0;
fld[mv.second.first][mv.second.second] = 1;
return fld;
}
// Recursive passage all the moves
void bruteforce(field fld)
{
static bool display = false;
static int lvl = 33;
static time_t counter = 0; // Num of checked field
++counter;
// Num 7000 is empirical
// Once we get the conclusion of the 7000, it allows the processor
// to be optimally loaded, and we see a progress
if ((counter % 7000) == 0)
{
display = true;
}
if ( counter > 33 )
{
int ibuf = path_to_win.size();
if (lvl > ibuf) lvl = ibuf;
}
std::list<move*> *b = get_all_moves(fld);
step buf;
if (b != nullptr)
{
buf = step(fld, b);
path_to_win.push_back(fld);
}
else
{
int res = IsWin(fld);
path_to_win.push_back(fld);
if (display == true)
{
system("cls");
std::cout << "Min level: " << lvl << "n<"
<< counter << '>' << "nCurrent result:n" << fld << std::endl;
display = false;
}
if (res == win_condition)
{
std::cout << "Num of checked fields: " << fld_buf.size() <<
"nSize of the path_to_win: " << path_to_win.size() << std::endl;
std::ofstream winpath_to_win("path_to_win.txt");
if (winpath_to_win)
{
for (std::list<field>::const_iterator it = path_to_win.begin(); it != path_to_win.end(); ++it)
{
winpath_to_win << (*it) << std::endl;
}
winpath_to_win.close();
}
for (std::list<field>::const_iterator it = path_to_win.begin(); it != path_to_win.end(); ++it)
{
std::cout << (*it) << std::endl;
}
system("pause");
}
path_to_win.pop_back();
return;
}
field fwithmove = nullptr;
for (
std::list<move*>::iterator it = buf.second->begin();
it != buf.second->end();
fwithmove = nullptr, buf.second->pop_front(), it = buf.second->begin()
)
{
fwithmove = copy_field(fwithmove, buf.first);
// Make move in copy of the buf.first field,
// buf.first field not changed and use to copy in next iteration
make_move(fwithmove, *(*it));
Field *f = new Field(fwithmove);
if (fld_buf.count(*f))
{
free_mem_from_field(fwithmove);
delete (*it);
continue;
}
else
fld_buf.insert(*f);
delete f;
bruteforce(fwithmove);
free_mem_from_field(fwithmove); // Free alloc memory for the fwithmove field, where we did move
delete (*it); // Free memory from under "move" in list<move*> which we did
}
path_to_win.pop_back();
delete buf.second;
}
public:
China_Checkers_Hack(const int _x = 7, const int _y = 7, const int wincondition = 1) : win_condition(wincondition)
{
x = _x;
y = _y;
field main_field;
if ((main_field = alloc_mem_for_field()) != nullptr)
{
init_field(main_field);
bruteforce(main_field);
free_mem_from_field(main_field);
}
else
message("Memory out, your computer gonna update RAM!");
}
~China_Checkers_Hack()
{
for (std::list<field>::iterator it = path_to_win.begin(); it != path_to_win.end(); ++it)
{
free_mem_from_field(*it);
}
}
};
}
int main(int argc, char* argv[])
{
China_Checkers::China_Checkers_Hack bruteforce;
system("pause");
return 0;
}
* * 1 0 1 * *
1 1 1 0 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 0 1 * *
1 0 0 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 0 1 * *
1 1 0 1 1 1 1
1 0 1 1 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 0 1 * *
0 0 1 1 1 1 1
1 0 1 1 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 1 1 * *
* * 1 0 1 * *
0 1 0 0 1 1 1
1 0 1 1 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 1 1 0 1 1 1
1 0 1 1 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
1 0 1 1 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
1 1 0 0 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
0 0 1 0 1 1 1
1 0 1 1 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
0 0 1 0 1 1 1
1 1 0 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
0 0 1 0 1 1 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
0 0 1 1 0 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 1 1 * *
* * 0 1 1 * *
0 0 0 0 1 1 1
0 0 1 0 0 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 1 * *
0 0 0 1 1 1 1
0 0 1 0 0 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 0 * *
0 0 0 1 0 1 1
0 0 1 0 1 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 0 * *
0 0 0 1 1 0 0
0 0 1 0 1 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 0 * *
0 0 0 0 0 1 0
0 0 1 0 1 0 1
0 0 1 0 1 1 1
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 0 * *
0 0 0 0 0 1 1
0 0 1 0 1 0 0
0 0 1 0 1 1 0
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 0 * *
0 0 0 0 1 0 0
0 0 1 0 1 0 0
0 0 1 0 1 1 0
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 1 * *
* * 0 0 1 * *
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 0 1 0 1 1 0
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 1 0 0
0 0 1 0 0 0 0
0 0 1 0 1 1 0
* * 1 1 1 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 1 0 0
0 0 1 0 1 0 0
0 0 1 0 0 1 0
* * 1 1 0 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 0 1 0 1 1 0
* * 1 1 0 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 0 1 1 0 0 0
* * 1 1 0 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 0 0 0 0 0
* * 1 1 0 * *
* * 1 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 1 0 0 0 0
0 1 1 0 0 0 0
* * 0 1 0 * *
* * 0 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 0 0 0 0 0
* * 1 1 0 * *
* * 0 1 1 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 0 0 0 0 0
* * 1 1 0 * *
* * 1 0 0 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 1 1 0 0 0 0
* * 0 1 0 * *
* * 0 0 0 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 1 0 0 0
* * 0 1 0 * *
* * 0 0 0 * *
* * 0 0 0 * *
* * 0 0 0 * *
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
* * 0 0 0 * *
* * 0 1 0 * *
Автор: Whiteha