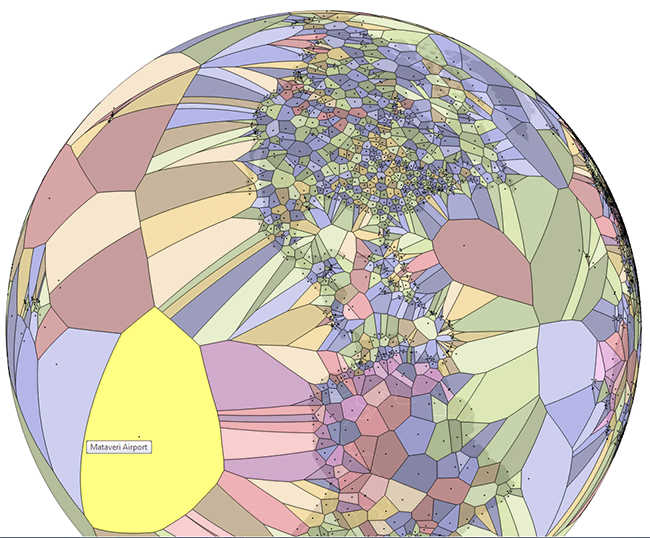
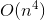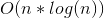Рубрика «диаграмма Вороного»

в 9:03, , рубрики: алгоритм Форчуна, Алгоритмы, диаграмма Вороного, математика, процедурная генерация, разработка игр

Последние несколько недель я работал над реализацией алгоритма Форчуна на C++. Этот алгоритм берёт множество 2D-точек и строит из них диаграмму Вороного. Если вы не знаете, что такое диаграмма Вороного, то взгляните на рисунок:

Алгоритм Форчуна, подробности реализации - 1

Для каждой входной точки, которая называется «местом» (site), нам нужно найти множество точек, которые ближе к этому месту, чем ко всем остальным. Такие множества точек образуют ячейки, которые показаны на изображении выше.

В алгоритме Форчуна примечательно то, что он строит такие диаграммы за время $O(nlog n)$ (что оптимально для использующего сравнения алгоритма), где $n$ — это количество мест.

Я пишу эту статью, потому что считаю реализацию этого алгоритма очень сложной задачей. На данный момент это самый сложный из алгоритмов, которые мне приходилось реализовывать. Поэтому я хочу поделиться теми проблемами, с которыми я столкнулся, и способами их решения.

Как обычно, код выложен на github, а все использованные мной справочные материалы перечислены в конце статьи.
Читать полностью »

в 8:02, , рубрики: svg, диаграмма Вороного, Дизайн игр, процедурная генерация карт, разработка игр, симуляция климата, триангуляция Делоне
image

Часть 1. SVG и системы координат

До недавнего времени размеры карт в моей игре Dragons Abound были фиксированными и несколько недетерминированными. Я считал их «региональными» — не картами всего мира, но его значительными частями, такими например, как западное побережье США или часть Европы. Меня вполне устраивал этот масштаб, но я хотел немного поэкспериментировать с игрой, чтобы посмотреть, смогу ли я генерировать карты целого мира (или хотя бы большего размера). Но прежде чем я приступлю к этому, давайте немного поговорим о картах фэнтези-миров.

Мир — это большое пространство. Большинство карт фэнтезийных «миров» даже близко не походят на истинный размер. Возьмём, например, Средиземье, в котором происходит действие «Властелина колец»:

Как я создавал карты континентов для своей игры - 2

Хоть и кажется, что на ней запечатлён огромный мир, на самом деле Средиземье создано на основе Европы.
Читать полностью »

в 8:01, , рубрики: voronoi, Алгоритмы, диаграмма Вороного, процедурная генерация, разработка игр, триангуляция Делоне, шум перлина, метки: , ,

Я хотел научиться генерировать интересные игровые карты, которые не обязательно были бы реалистичными, а также попробовать техники, с которыми раньше не работал. Обычно я создаю карты с другой структурой. Что можно сделать с тысячей полигонов вместо миллиона тайлов? Отчётливо различимые игроком области могут быть полезны для геймплея: местоположения городов, места квестов, территории для захвата или колонизации, ориентиры, точки поиска пути, зоны с разной сложностью и т.д. Я генерировал карты с помощью полигонов, а затем растеризировал их вот в такие карты:

image

Во многих процедурных генераторах карт, в том числе и некоторых моих предыдущих проектах, для генерирования карты высот используются функции шума (midpoint displacement, фракталы, diamond-square, шум Перлина и т.д.). Здесь я их не применял. Вместо неё я использовал структуру графов для моделирования элементов, определяемых ограничениями геймплея (высота, дороги, течение рек, места квестов, типы монстров) и функции шума для моделирования того, что не ограничивается геймплеем (форма побережья, расположение рек и деревьев).
Читать полностью »

в 16:51, , рубрики: c++, stl, алгоритм Форчуна, Алгоритмы, диаграмма Вороного, математика, Спортивное программирование

Приветствую, уважаемые читатели данной статьи! В статье я дам описание имплементации алгоритма Форчуна (англ. Fortune's algorithm) для построения диаграммы Вороного (англ. Voronoi diagram) с использованием нативных сбалансированных двоичных деревьев поиска (для уникальных элементов) (англ. BST, binary search tree), предусмотренных стандартом C++, — ассоциативных упорядоченных контейнеров std::map и std::set.

Читать полностью »

в 15:58, , рубрики: c++, алгоритм Форчуна, Алгоритмы, береговая линия, вычислительная геометрия, геометрия, диаграмма Вороного, заметающая прямая, пересечение многоугольников, пересечение отрезков, пересечение парабол, пересечение прямых

Доброго всем времени суток, уважаемые посетители сайта Хабрахабр. В данной статье я бы хотел рассказать вам о том, что такое диаграмма Вороного (изображена на картинке ниже), о различных алгоритмах её построения (за Диаграмма Вороного и её применения - 1, Диаграмма Вороного и её применения - 2 — пересечение полуплоскостей, Диаграмма Вороного и её применения - 3 — алгоритм Форчуна) и некоторых тонкостях реализации (на языке C++).

Диаграмма Вороного и её применения - 4

Также будет рассмотрено много интересных применений диаграммы и несколько любопытных фактов о ней. Будет интересно!
Читать полностью »

в 23:36, , рубрики: Демосцена, диаграмма Вороного, Инфографика, карта мира, столицы, метки: , ,

Диаграммы Вороного для аэропортов и столиц - 1

Диаграмма Вороного конечного множества точек S на плоскости представляет такое разбиение плоскости, при котором каждая область этого разбиения образует множество точек, более близких к одному из элементов множества S, чем к любому другому элементу множества.

Эксперт по визуализации данных и информатике Джейсон Дэвис (Jason Davies) на своём сайте выложил несколько любопытных экспериментов, в том числе со сферическими диаграммами Вороного.
Читать полностью »

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js