Здравствуйте, меня зовут Николай Стрекопытов и я придумал как подбирать гиперпараметры бескомпромиссно лучше GridSearch’а. Нужно лишь изменить порядок вычислений. И да, это заявка на обновление индустриального стандарта - скоро вы сможете улучшить свои ML-пайплайны заменой нескольких строчек кода.
Рубрика «методы оптимизации»
Пора забывать GridSearch — встречайте ProgressiveGridSearch. Фракталы в ML, постепенно увеличиваем разрешение
2023-03-31 в 16:18, admin, рубрики: open source, python, искусственный интеллект, математика, машинное обучение, методы оптимизации, нейронные сети, подбор гиперпарметров, сезон machine learningКвазиньютоновские методы, или когда вторых производных для Атоса слишком много
2019-10-08 в 12:26, admin, рубрики: BFGS, DFP, Алгоритмы, квазиньютоновские методы, математика, машинное обучение, методы оптимизацииПри первом знакомстве с квазиньютоновскими методами можно удивиться дважды. Во-первых, после беглого взгляда на формулы охватывают сомнения, что это вообще может работать. Однако же они работают. Дальше кажется сомнительным, что они будут работать хорошо. И тем удивительнее видеть то, насколько они превосходят по скорости разнообразные вариации градиентного спуска, причем не на специально построенных задачах, а на самых настоящих, взятых из практики. И если после этого еще остаются сомнения вперемешку с интересом — то нужно разбираться в том, почему вообще работает это нечто.
Читать полностью »
Как работает метод Левенберга-Марквардта
2019-10-04 в 19:28, admin, рубрики: trust-region, Алгоритмы, задача наименьших квадратов, математика, машинное обучение, метод доверительного региона, метод Левенберга-Марквардта, методы оптимизацииАлгоритм Левенберга-Марквардта прост. Алгоритм Левенберга-Марквардта эффективен.
А еще о нем говорят, что он где-то посередине между градиентным спуском и методом Ньютона, что бы это не значило. Ну, с методом Ньютоном и его связью с градиентным спуском вроде как разобрались. Но что имеют ввиду когда произносят эту глубокомысленную фразу? Попробуем слегка подразобраться.
Читать полностью »
Ох уж этот метод Ньютона
2019-10-02 в 19:01, admin, рубрики: trust-region, Алгоритмы, градиентный спуск, математика, машинное обучение, метод доверительного региона, метод ньютона, методы оптимизацииО методах численной оптимизации написано много. Это и понятно, особенно на фоне тех успехов, которые в последнее время демонстрируют глубокие нейронные сети. И очень отрадно, что хотя бы часть энтузиастов интересуется не только тем, как забомбить свою нейросеточку на набравшей в этих ваших интернетах популярность фреймворках, но и тем, как и почему все это вообще работает. Однако мне в последнее время пришлось отметить, что при изложении вопросов, связанных с обучением нейросетей (и не только с обучением, и не только сетей), в том числе на Хабре, все чаще впроброс используется ряд “хорошо известных” утверждений, справедливость которых, мягко говоря, сомнительна. Среди таких сомнительных утверждений:
- Методы второго и более порядков плохо работают в задачах обучения нейросетей. Потомучто.
- Метод Ньютона требует положительной определенности матрицы Гессе (вторых производных) и поэтому плохо работает.
- Метод Левенберга-Марквардта — компромисс между градиентным спуском и методом Ньютона и вообще эвристичекий.
и т.д. Чем продолжать этот список, лучше перейдем к делу. В этом посте рассмотрим второе утверждение, поскольку его я только на Хабре встречал как минимум дважды. Первый вопрос затрону только в той части, что касается метода Ньютона, поскольку он куда более обширен. Третий и остальные оставим до лучших времен.
Читать полностью »
Выявление скрытых зависимостей в данных для повышения качества прогноза в машинном обучении
2017-10-03 в 16:16, admin, рубрики: data mining, машинное обучение, методы оптимизацииПлан статьи
- Постановка задачи.
- Формальное описание задачи.
- Примеры задач.
- Несколько примеров на синтетических данных со скрытыми линейными зависимостями.
- Какие ещё скрытые зависимости могут содержаться в данных.
- Автоматизация поиска зависимостей.
- Число признаков меньше пороговой величины.
- Число признаков превышает пороговую величину.
Постановка задачи
Нередко в машинном обучении встречаются ситуации, когда данные собираются априори, и лишь затем возникает необходимость разделить некоторую выборку по известным классам. Как следствие часто может возникнуть ситуация, когда имеющийся набор признаков плохо подходит для эффективной классификации. По крайней мере, при первом приближении.
В такой ситуации можно строить композиции слабо работающих по отдельности методов, а можно начать с обогащения данных путём выявления скрытых зависимостей между признаками. И затем строить на основе найденных зависимостей новые наборы признаков, некоторые из которых могут потенциально дать существенный прирост качества классификации.
Формальное описание задачи
Перед нами ставится задача классификации L объектов, заданных n вещественными числами. Мы будем рассматривать простой двухклассовый случай, когда метки классов — это −1 и +1. Наша цель — построить линейный классификатор, то есть такую функцию, которая возвращает −1 или + 1. При этом набор признаковых описаний таков, что для объектов противоположных классов, измеренных на данном множестве признаков, практически не работает гипотеза компактности, а разделяющая гиперплоскость строится крайне неэффективно.
Иными словами, всё выглядит так, будто задача классификации на данном множестве объектов не может быть решена эффективно.
Читать полностью »
Решение прямой и двойственной задачи линейного программирования средствами Python
2017-08-27 в 11:20, admin, рубрики: python, scipy. optimize, двойственные задачи, Задачи линейного программирования, математика, методы оптимизации, разработка под windowsВведение
Следует отметить, что методы решения задач линейного программирования относятся не к экономике, а к математике и вычислительной технике. При этом экономисту нужно обеспечить максимально комфортные условия диалога с соответствующим программным обеспечением. В свою очередь такие условия могут обеспечивать только динамично развивающиеся и интерактивные среды разработки, имеющие в своём арсенале набор необходимых для решения таких задач библиотек. Одной из каких сред разработки программного обеспечения безусловно является Python.
Постановка задачи
В публикациях [1,2] рассматривались решения прямых задач оптимизации методом линейного программирования и был предложен обоснованный выбор решателя scipy. optimize.
Однако известно [3], что каждой задаче линейного программирования соответствует так называемая выделенная(двойственная)задача. В ней по сравнению с прямой задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или наоборот, вместо минимума — максимум). Задача, двойственная к двойственной — эта сама исходная задача.
Решение двойственной задачи очень важно для анализа использования ресурсов. В данной публикации будет доказано, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной).
Оптимальные значения стоимости материала и труда будут оцениваться по их вкладу в целевую функцию. В результате будут получены «объективно обусловленные оценки» сырья и рабочей силы, которые не совпадают с рыночными ценами.Читать полностью »
Умеют ли коты строить регрессию?
2017-06-20 в 14:04, admin, рубрики: scala, Алгоритмы, линейная регрессия, математика, машинное обучение, методы оптимизации, Программирование, эвристические алгоритмыДоброго времени суток! Пора вновь вернуться к задачам оптимизации. На этот раз мы займемся линейной регрессией и разберемся, кто же такие коты — только пушистые домашние мерзавцы животные или еще и неплохой инструмент для решения прикладных задач.

Прикладное применение задачи нелинейного программирования
2017-05-15 в 5:43, admin, рубрики: k-means, random search, scala, Алгоритмы, кластеризация, математика, машинное обучение, методы оптимизации, оптимальное управление, Программирование, эвристические алгоритмыДоброго времени суток!
В свое время, будучи студентом младших курсов, я начал заниматься научно-исследовательской работой в области теории оптимизации и синтеза оптимальных нелинейных динамических систем. Примерно в то же время появилось желание популяризировать данную область, делиться своими наработками и мыслями с людьми. Подтверждением этому служит пара-тройка моих детских незрелых статей на Хабре. Тем не менее, на тот момент эта идея оказалась для меня непосильной. Возможно ввиду моей занятости, неопытности, неумения работать с критикой и советами или чего-то еще. Можно до бесконечности пытаться найти причину, но ситуацию это не изменит: я забросил эту идею на полку, где она благополучно лежала и пылилась до этого момента.
Закончив специалитет и готовясь к защите кандидатской диссертации, я задался вполне логичным вопросом: «а что же дальше?» Имея за плечами опыт как обычной работы, так и исследовательской, я вновь вернулся к той самой идее, которая, казалось бы, должна была утонуть под толщей пыли. Но вернулся я к этой идее в более осознанной форме.
Я решил заняться разработкой программного обеспечения, связанного с той отраслью, которой занимаюсь уже на протяжении 8 лет, и моими личными академическими пристрастиями, которые включают в себя методы оптимизации и машинное обучение.

Ну что ж, всем заинтересовавшимся:
Читать полностью »
Алгоритм Левенберга — Марквардта для нелинейного метода наименьших квадратов и его реализация на Python
2016-08-26 в 16:16, admin, рубрики: curve-fitting, data mining, Алгоритмы, математика, машинное обучение, метод наименьших квадратов, методы оптимизации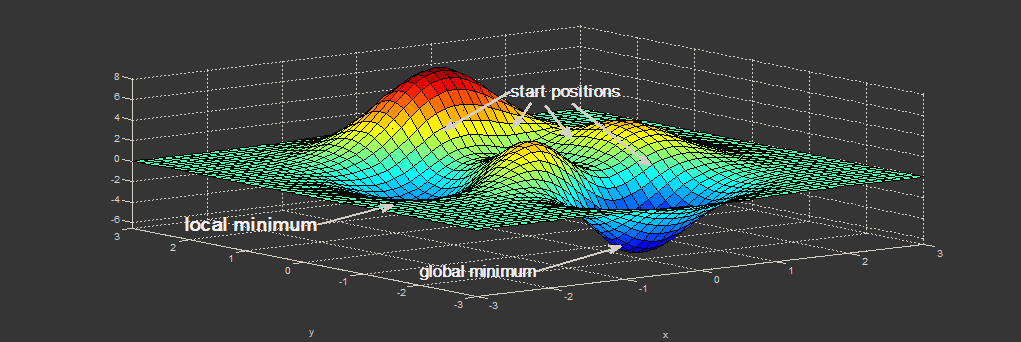
Нахождение экстремума (минимума или максимума) целевой функции является важной задачей в математике и её приложениях (в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.
Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов(МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде:

Алгоритм Левенберга — Марквардта используется для решения нелинейного метода наименьших квадратов. Статья содержит:
- объяснение алгоритма
- объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
- приведена реализация на Python с исходниками на github
- сравнение методов
Алгоритм TILT или нестандартное использование ранга матрицы
2014-12-10 в 10:18, admin, рубрики: computer vision, линейная алгебра, методы оптимизации, обработка изображений Сегодня мы рассмотрим алгоритм TILT (Transform Invariant Low-rank Texture) и множество его методов применения в области Computer Vision. Статья будет нести несколько обзорный характер, без плотного углубления в математические дебри.
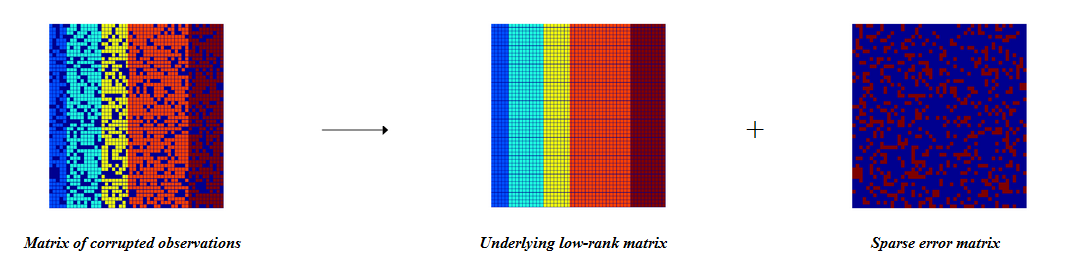
Читать полностью »
