Многие из вас, я уверен, слышали о теории игр в какой-то момент своей жизни. Если вы хотите выглядеть умным и произвести впечатление на свою девушку — просто упомяните «игру с нулевой суммой» или «эволюционную стратегию», и ваши шансы отвести её домой сегодня вечером только что подскочили на 50%. Или вы можете использовать теорию игр, чтобы принимать решения в инвестировании своих денег (чтобы их полностью потерять и разориться) или, например решая, на какой девушке жениться (что также очень вероятно вас разорит). Как видите, это очень полезная теория.
Рубрика «теория игр»
Теория игр за 15 минут
2024-01-22 в 5:30, admin, рубрики: логика, логические игры, системы принятия решений, теория игрКритерий Келли
2023-07-27 в 17:57, admin, рубрики: венчурные инвестиции, Занимательные задачки, Критерий Келли, математика, теория игрВведение
От умного риска до победы близко. Кто не рискует, тот не пьет шампанского. Без риска и жизнь пресна.
Вероятность выигрыша в покере
2021-09-04 в 6:28, admin, рубрики: математика, математическая статистика, Статистика в IT, теория игрНекоторое время назад обратились ко мне с вопросом, как сделать программу, которая будет выигрывать в покер. После некоторого количества обсуждений, заказчик не захотел узнавать результат моих размышлений на эту тему, посчитал что дорого. Поэтому я разместил эти свои размышления здесь и за бесплатно.
Сразу оговорюсь, что я в покер не играю, и знаю его хуже чем те, кто играет свои первые партии в жизни. Но может это не так уж и важно?
Рассматриваю тот покер, где в колоде 52 карты: 2-10, В, Д, К, Т и 4 масти. Вероятно это Техаский Холдем. На столе в последнем круге пять карт, и по две карты у игроков.
Kaboom: необычный сапёр
2020-02-11 в 8:02, admin, рубрики: Алгоритмы, Блог компании Cloud4Y, логические игры, математика, ненормальное программирование, разработка игр, сапёр, теория игр
В детстве я три раза в неделю по часу-полтора сидел на работе у отца. Меня пускали за компьютер, где из развлечений был лишь сапёр и Paint. Рисовать мне быстро надоедало, зато желание открыть всё поле и не взорваться мотивировало искать новые и новые способы прохождения этой игры. Спустя много лет я случайно наткнулся на интересную статью про клона сапёра, и не мог пройти мимо. Предлагаю и вам ознакомиться с ней. Это история о разработке Kaboom, клона легендарной игры Сапёр с собственной изюминкой.Читать полностью »
Реализация алгоритмической теории игр на Python с Nashpy
2020-02-05 в 13:52, admin, рубрики: python, Алгоритмы, Блог компании Leader-ID, математика, Программирование, теория игрТеория игр — это метод изучения стратегических ситуаций, когда результаты зависят не только от ваших действий, но и от того, что предпримут другие.
Что такое стратегическая ситуация? Вспомним типы рыночных структур: есть совершенная конкуренция, когда все компании являются ценообразующими, то есть им не нужно беспокоиться о стратегии формирования цены, и есть монополия, когда на рынке только одна компания, которая устанавливает свои цены. Так вот: все, что между совершенной конкуренцией и монополией, является стратегической ситуацией.
Алгоритмическая теория игр находится на стыке теории игр и компьютерной науки и направлена на изучение и создание алгоритмов для стратегий.
Под катом короткий рассказ про то, как можно задействовать теорию игр на Python при помощи библиотеки Nashpy.
Алексей Савватеев: Теоретико-игровая модель социального раскола (+ опрос по nginx)
2019-12-15 в 15:31, admin, рубрики: математика, модель социального раскола, Научно-популярное, Савватеев, социальный конфликт, теория игр, Учебный процесс в IT Привет!
Меня зовут Ася. Нашла очень крутую лекцию, не могу не поделиться.
Предлагаю вашему вниманию конспект видеолекции о социальных конфликтах на языке математиков-теоретиков. Полная лекция доступна по ссылке: Модель социального раскола: игра тернарного выбора на сетях взаимодействия (А. В. Леонидов, А. В. Савватеев, А. Г. Семёнов). 2016.

Алексей Владимирович Савватееев — кандидат экономических наук, доктор физико-математических наук, профессор МФТИ, ведущий научный сотрудник РЭШ.
В данной лекции я расскажу о том, как математики и теоретики-игровики смотрят на повторяющийся социальный феномен, примерами которого являются голосование за выход Англии из Евросоюза (англ. Brexit), явление глубокого социального раскола в России после Майдана, выборы в США с сенсационным исходом.
Как можно смоделировать подобные ситуации, чтобы в них были отголоски реальности? Чтобы понять феномен, необходимо изучать его всесторонне, но в этой лекции будет модель.
Читать полностью »
Игра в собеседование
2019-12-12 в 23:42, admin, рубрики: интервью, математика, матстатистика, никто не читает теги, собеседования, теория игр, управление персоналом, управление проектамиПару недель назад я случайно открыл резюме всему интернету и прошел пару собеседований. Это навело меня на мысли о процессе отбора в целом.
В идеальном мире я бы хотел чтобы собеседование отнимало у меня как можно меньше времени. И мне нужно, чтобы я устраивался только в подходящие мне компании. Не хочется искать работу через месяц после выхода на предыдущую. Но как себя вести, чтобы добиться этого?
С другой стороны, мне может потребоваться собеседовать кандидата. И приоритеты у меня все те же. Я не хочу тратить много времени и мне необходимо избежать ситуаций с увольнением нового сотрудника по причине непригодности или по собственному желанию.
Держа в голове все вышесказанное, я начал анализировать процесс отбора кандидатов с обеих сторон. У меня в запасе был небольшой курс по теории игр, щепотка матстатистики и здравый смысл. А результаты — под катом.
Читать полностью »
Математическое обоснование нецелесообразности бежать вниз по эскалатору в метро
2019-10-26 в 17:45, admin, рубрики: математика, теория вероятностей, теория игрВопреки правилам пользования метрополитеном, желая сэкономить время, каждый из нас хотя бы раз в жизни бежал вниз по эскалатору. На первый взгляд кажется, что это абсолютно логично и правильно: хочешь быстрее уехать – постарайся оказаться на платформе как можно раньше. Однако, практически сразу в голову приходит следующий сценарий: вы сломя голову летите по эскалатору вниз, спускаетесь на платформу, а двери вагона закрываются прямо перед вашим носом. Пока вы ждёте следующий поезд – люди, которые вставали на эскалатор одновременно с вами, успевают стоя на месте спокойно спуститься и сесть в следующий поезд. В таком случае – выигрыша никакого. Так насколько же рационально бежать по эскалатору вниз и стоит ли заниматься этим вообще? Спешу вас обрадовать – ответ найден! Ниже представлено математическое обоснование нецелесообразности (да, именно НЕ) бежать вниз по эскалатору в метро.
Читать полностью »
Алексей Савватеев и теория игр: «Какова вероятность, что в ближайшие пять лет будет скинута атомная бомба?»
2019-06-09 в 12:02, admin, рубрики: Алгоритмы, Занимательные задачки, математика, Научно-популярное, парадокс Браеса, Савватеев, теория игр, Учебный процесс в IT
Расшифровка видеозаписи лекции.
Теория игр — дисциплина, которая прочно зависла между математикой и социальными науками. Одним канатом к математике, другим канатом — к социальным наукам, прочно прикреплена.
В ней есть теоремы, достаточно серьёзные (теорема существования равновесия), про неё снят фильм «Игры разума», теория игр проявляется в множестве художественных произведений. Если смотреть вокруг, то и дело встречаешь игровую ситуацию. Я собрал несколько сюжетов.
Все мои презентации делает жена. Все презентации могут свободно распространяться, я буду крайне рад, если вы по ней будете читать лекции. Это полностью свободный материал.
Некоторые сюжеты спорные. Модели могут быть разные, можете не соглашаться с моей моделью.
- Теория игр в Талмуде.
- Теория иг в русской классике.
- Телеигра или задача о парковочных местах.
- Люксембург в Евросоюзе.
- Синдзо Абэ и Северная Корея
- Парадокс Брайеса в Метрогородке (Москва)
- Два парадокса Дональда Трампа
- Рациональное безумие (снова Северная Корея)
(В конце поста — опрос про бомбу.)
Читать полностью »
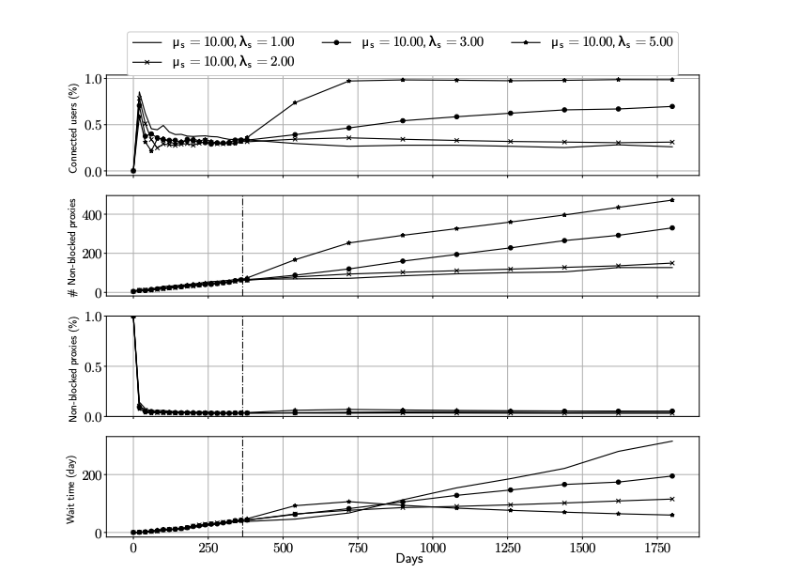
Исследование: создание устойчивого к блокировкам прокси-сервиса с помощью теории игр
2019-05-23 в 15:11, admin, рубрики: Блог компании INFATICA.io — глобальная пиринговая прокси сеть для бизнеса, информационная безопасность, исследование, обход блокировок, прокси, Сетевые технологии, теория игрНесколько лет назад международная группа ученых из университетов Массачусетса, штата Пенсильвания и немецкого Мюнхена провела исследование эффективности традиционных прокси в качестве инструмента борьбы с цензурой. В результате ученые предложили новый метод обхода блокировок, основанный на теории игр. Мы подготовили адаптированный перевод основных моментов этой работы.Читать полностью »