Или как можно проще об основных принципах ООП в Lazarus и FreePascal
Часть I
Изучать ООП (объектно-ориентированное программирование) можно двумя способами: или прочитать сотню книжек, в которых дается голая теория об устройстве классов и принципах наследования, полиморфизма, инкапсуляции, но так ничему и не научиться, или перестать беспокоиться и попытаться на практике освоить новые приемы, переработав, к примеру, готовые коды, а лучше с нуля изготовив что-то простое, но красивое.
Во всех книгах, посвященных паскалю, delphi и lazarus (я нашел аж целых две о последнем), очень схожая часть, посвященная ООП. По этим книгам можно много узнать о том, насколько круче ООП устаревшего структурного подхода, но так и не получить достаточных навыков применения этого на практике. Конечно, любой программист, использующий визуальные IDE, уже по умолчанию использует ООП, так как все компоненты и структурные элементы визуального приложения представляют собой объекты, однако свои собственные структуры и абстракции перенести в парадигму ООП бывает очень сложно. Чтобы понять всю прелесть и оценить открывающиеся перспективы, я решил сделать небольшое приложение, которое в конечном итоге превратилось в простенький screensaver. Заодно вспомнил о существовании тригонометрии.
Приложение будет рисовать на экране в случайных местах пятьдесят полярных роз с разными характеристиками: размер, цвет, количество лепестков. Потом их же затирать и рисовать новые, и т.д. Используя принципы структурного программирования, можно, конечно, сделать обычный многомерный массив объемом на 50 и в нем сохранять все уникальные характеристики. Однако стоит вспомнить, что паскаль подразумевает строгую типизацию данных, а, следовательно, массив не может состоять их элементов с разными типами. Можно сделать массив из записей (record), но чего уж мелочиться, от записи до класса — один шаг. Вот его мы и сделаем.
Важный принцип ООП — инкапсуляция. Это значит, что класс должен скрывать внутри себя всю логику своей работы. Наш класс, назовем его TPetal, имеет поля с разным типом данных, которые определяют уникальные характеристики (координаты центра, размер, коэффициенты для уравнения полярной розы, цвет), и методы работы. Все другие элементы программы должны лишь вызывать эти методы, не вникая в подробности их реализации. Пока класс должен уметь нарисовать себя и стереть. Для начала достаточно:
{ TPetal }
TPetal = class
private
R, phi: double;
X, Y, CX, CY: integer;
Scale, RColor, PetalI: integer;
public
constructor Create (Xmax, Ymax: integer);
procedure Draw (Canvas: TCanvas; Erase: boolean = FALSE);
end;
Конструктор класса имеет два параметра — это границы канвы, на которой будет происходить рисование. Реализация конструктора следующая:
constructor TPetal.Create(Xmax, Ymax: integer);
begin
inherited Create;
CX:=Random(Xmax);
CY:=Random(Ymax);
RColor:=1+Random($FFFFFF);
Scale:=2+Random(12);
PetalI:=2+Random(6);
end;
Любой рукотворный класс в Delphi/Lazarus является прямым или опосредованным потомком класса TObject, и при создании объектов своего класса нужно обязательно вызвать конструктор родителя, чтобы объект правильно создался и под него выделилась память компьютера. Поэтому в начале своего конструктора мы вызываем конструктор родителя. После мы случайным образом генерируем уникальные характеристики своей полярной розы: координаты центра, цвет, коэффициент масштаба и коэффициент, определяющий количество лепестков.
Дальше метод рисования. Как вы видете, чтобы нарисовать или стереть объект я написал единственный метод, в котором имеется второй параметр и по умолчанию он имеет значение FALSE. Это связано с тем, что нарисовать и стереть — одна и та же операция, только рисуется объект случайным цветом, а стирается — черным. При вызове метода из программы без использования второго параметра объект рисуется, а при использовании параметра Erase — объект стирается:
procedure TPetal.Draw(Canvas: TCanvas; Erase: boolean);
begin
phi:=0;
if Erase then RColor:=clBlack;
with Canvas do
while phi < 2*pi do
begin
R:=10*sin(PetalI*phi);
X:=CX+Trunc(Scale*R*cos(phi));
Y:=CY-Trunc(Scale*R*sin(phi));
Pixels[X,Y]:=RColor;
phi+=pi/1800;
end;
end;
Для рисования лепестков используется функция полярной розы в полярной системе координат:
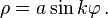
где ρ определяет радиальную координату, а φ — угловую. α — это коэффициент, определяющий длину лепестков. В нашей формуле коэффициент сразу равен 10, чтобы розы не получались слишком мелкими. Угловая координата у нас пробегает от 0 до 2π, чтобы захватить все 360 градусов (цикл while). А после получения радиальной координаты мы вычисляем декартовы: x и y, чтобы отрисовать эту точку на канве (поразитесь в очередной раз, насколько быстро современные компьютеры производят вычисления: внутри метода длиннющий цикл, в котором тригонометрические вычисления; вспомните, как «быстро» рисовал подобное Zx-spectrum). Коэффициент k в формуле (в программе — PetalI) определяет количество лепестков. У нас пока для простоты используются только целые числа, поэтому все розы получаются гипотрохоидные с неперекрывающимися лепестками.
Итак, наш класс реализован и все нужные навыки он имеет. Пришло время использовать. В главном модуле приложения в первую очередь нам нужно объявить массив из 50 объектов класса TPetal, потом на форму кидаем Image и Timer, изображение растягиваем на всю форму (Client), а у таймера устанавливаем период срабатывания в 100 миллисекунд. Метод таймера будет такой:
var
Form1: TForm1;
Marg: boolean;
Petals: array [0..49] of TPetal;
CurPetal: smallint;
//-----------------------------------------------------------------------------------
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if not Marg then
begin
Petals[CurPetal]:=TPetal.Create(img.Width,img.Height);
Petals[CurPetal].Draw(img.Canvas);
CurPetal+=1;
if CurPetal=50 then Marg:=TRUE;
end else begin
Petals[50-CurPetal].Draw(img.Canvas,TRUE);
Petals[50-CurPetal].Free;
CurPetal-=1;
if CurPetal=0 then Marg:=FALSE;
end;
img.Canvas.TextOut(10,10,IntToStr(CurPetal)+' ');
end;
Как видно я использовал еще пару глобальных переменных: CurPetal — счетчик объектов, принимает значения от 0 до 50 и обратно; Marg — сигнализатор границ счетчика, но из логики работы метода все должно быть предельно понятно.
Если бы мы использовали парадигму структурного программирования, то внутри обработчика таймера нам нужно было бы самостоятельно инициализировать все характеристики уникальной розы, отрисовать её, а затем стирать. Метод бы разросся и стал бы не наглядным. Но теперь у нас есть класс, который делает всё сам — конструктор класса сразу же инициализирует все характеристики, а метод класса DrawPetal инкапсулирует всю логику вычислений и отрисовки, для чего ему всего лишь передается указатель на необходимый объект, имеющий свойство Canvas (а это любая форма, и почти любой компонент). В итоге получается такой симпатичный screensaver:
Исследуя следующий принцип ООП — наследование, в дальнейшем можно от класса TPetal породить потомка, к примеру TOverlappingPetal, в котором полярная роза будет с перекрывающимися лепестками. Для этого (в целях универсализации) в классе-предке нужно изменить тип поля PetalI на действительное число, а конструктор потомка перегрузить так, чтобы это поле могло инициализироваться случайным дробным числом по соответствующим правилам.
Файлы проекта я сохранил в своем хранилище bitbucket, и для каждого этапа создал отдельную ветку. Пример выше вы найдете в ветке lesson1.
Часть II
Теперь предлагаю сделать то, на чём мы остановились. Итак, у нас есть класс TPetal, который умеет рисовать полярную розу с количеством лепестков от 3 до 16. Однако все объекты у нас получаются с неперекрывающимися лепестками. Меж тем, если посмотреть на табличку ниже, мы увидим, что разновидностей их больше. Форма определяется коэффициентом, равным n/d:
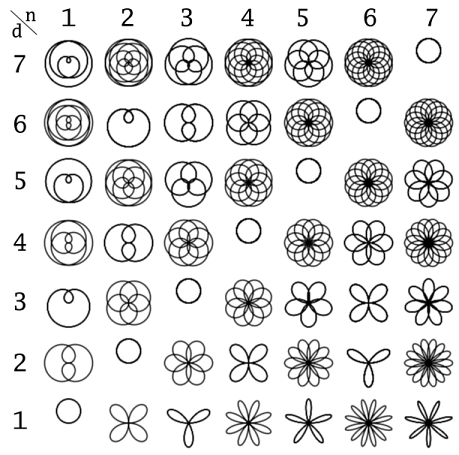
Породим потомка от класса TPetal:
{ TPetal }
TPetal = class
private
R, phi, PetalI: double;
X, Y, CX, CY: integer;
Scale, RColor: integer;
public
constructor Create (Xmax, Ymax: integer);
procedure Draw (Canvas: TCanvas; Erase: boolean = FALSE); overload;
end;
{ TOverlappedPetal }
TOverlappedPetal = class (TPetal)
public
constructor Create (Xmax, Ymax: integer);
procedure Draw (Canvas: TCanvas; Erase: boolean = FALSE); overload;
end;
В классе TOverlappedPetal мы добавляем свой конструктор, который будет действовать вместе с конструктором предка, а также перегруженный метод DrawPetal (на самом деле в конце мы обойдемся вообще без него, однако в настоящий момент — это хороший способ продемонстрировать перегрузку методов в наследниках класса). Вот реализация:
{ TOverlappedPetal }
constructor TOverlappedPetal.Create(Xmax, Ymax: integer);
begin
inherited Create (Xmax,Ymax);
while PetalI=Round(PetalI) do
PetalI:=(1+Random(6))/(1+Random(6));
end;
procedure TOverlappedPetal.Draw(Canvas: TCanvas; Erase: boolean);
begin
phi:=0;
if Erase then RColor:=clBlack;
with Canvas do
while phi < 12*pi do
begin
R:=10*sin(PetalI*phi);
X:=CX+Trunc(Scale*R*cos(phi));
Y:=CY-Trunc(Scale*R*sin(phi));
Pixels[X,Y]:=RColor;
phi+=pi/1800;
end;
end;
Видно, что конструктор класса TOverlappedPetal использует метод предка (inherited), но потом меняет значение поля PetalI, которым и задается коэффициент, влияющий на форму розы. При вычислении поля мы исключаем целые числа, чтобы не дублировать формы, уже имеющиеся у предка TPetal.
Файлы этого примера можно найти в ветке lesson2 в хранилище.
Теперь, если внимательно приглядеться, станет ясно, что хоть мы и программеры с ОО-мышлением, всё же мы по-прежнему недотягиваем до тру-программеров, так как реализация методов DrawPetal у предка и потомка практически идентична, а это первый по степени вызываемого butthurt любого гуру рефакторинга — повторяющийся кот код.

Разница реализаций — лишь в коэффициенте, умноженном на число π (2 или 12). Выносим этот коэффициент в отдельное поле предка TPetal (поле K), убираем излишнюю теперь перегрузку метода DrawPetal и получаем следующую структуру наших классов:
{ TPetal }
TPetal = class
private
R, phi, PetalI: double;
X, Y, K, CX, CY: integer;
Scale, RColor: integer;
public
constructor Create (Xmax, Ymax: integer);
procedure Draw (Canvas: TCanvas; Erase: boolean = FALSE);
end;
{ TOverlappedPetal }
TOverlappedPetal = class (TPetal)
public
constructor Create (Xmax, Ymax: integer);
end;
Хоть потомок TOverlappedPetal и отличается теперь от предка TPetal только своим конструктором, мы наглядно и полноценно продемонстрировали все принципы объектно-ориентированного программирования:
— инкапсуляция (вся работа класса находится внутри себя, внешняя связь с классом — только парой методов и передачей необходимого минимума параметров);
— наследование (мы породили от класса розы с неперекрывающимися лепестками класс розы с перекрывающимися лепестками);
— минимально, полиморфизм (мы продемонстрировали перегрузку методов — одно название, но разная реализация, но настоящую мощь полиморфизма я планирую продемонстрировать позже).
Вот какая реализация классов получилась в итоге:
constructor TOverlappedPetal.Create(Xmax, Ymax: integer);
begin
inherited Create (Xmax,Ymax);
K:=12;
while PetalI=Round(PetalI) do
PetalI:=(1+Random(6))/(1+Random(6));
end;
{ TPetal }
constructor TPetal.Create(Xmax, Ymax: integer);
begin
inherited Create;
CX:=Random(Xmax);
CY:=Random(Ymax);
K:=2;
RColor:=1+Random($FFFFF0);
Scale:=2+Random(12);
PetalI:=2+Random(6);
end;
procedure TPetal.Draw(Canvas: TCanvas; Erase: boolean);
begin
phi:=0;
if Erase then RColor:=clBlack;
with Canvas do
while phi < K*pi do
begin
R:=10*sin(PetalI*phi);
X:=CX+Trunc(Scale*R*cos(phi));
Y:=CY-Trunc(Scale*R*sin(phi));
Pixels[X,Y]:=RColor;
phi+=pi/1800;
end;
end;
Использовал я новые конструкции так: дополнил программу вторым массивом на 50 объектов класса TOverlappedPatel, кинкул второй таймер с периодом срабатывания 166 миллисекунд, прописал в его обработчик примерно такой же код, как у первого таймера. Из-за возникаемой между таймерами задержки визуально screensaver даже стал работать немного приятнее:
Как можно улучшить программу? Как раз с помощью третьего кита ООП — полиморфизма. Сейчас у нас программа выполняет двойную работу, а процессор обливается потом, непрерывно производя тригонометрические вычисления (ну у кого как, наверно). А можно ли создать единый массив объектов, но разных классов? Об этом и будет следующая часть, а код из примера выше — в ветке lesson2-1.
Часть III
Обычно в книгах по паскалю, delphi и lazarus описанию полиморфизма отводится пара страниц (в лучшем случае), не считая листинги кода (не считая, потому что от пары страниц текста понимание этих листингов не приходит). И поскольку книги по паскалю традиционно пишутся для студентов, все примеры кочуют из одного издания в другое и связаны с описанием абстрактного класса Человек и двух его наследников Студент и Преподаватель. Так как я не являюсь ни тем, ни другим, мне так и не удалось из этих книг почерпнуть знания о полиморфизме. Где бы можно было применить на практике классы Студентов и Преподавателей, чтобы понять сущность полиморфизма, я так и не придумал, поэтому пришлось постигать всё снова методом тыка.
Очень существенным недостатком всех этих книг я бы назвал то, что в главах о полиморфизме главным считается вопрос «как», хотя первостепенным является вопрос «зачем», ибо ответ на него поглощает 99% всей сути полиморфизма. Такой ответ я нашёл в чудесной статье Всеволода Леонова в блогах Embarcadero (текущее название владельца delphi). А в общих чертах полиморфизм представлен, например, так: есть базовый абстрактный класс Кошачьи, от которого порождены многочисленные наследники — Котик, Леопардик, Тигра, Лёва и т.д. Все они имеют схожие свойства, но методы их существования разные. Метод «мяу», к примеру, будет разным у котика и тигры. Метод базовго класса «поиграться» у котика перекрывается методом с реализацией «потереться об ноги», а вот у лёвы он перекрыт реализацией «сожрать руку». Однако все конкретные кошки будут являться объектами класса Кошачьи, и неопытный ребёнок будет настойчиво вызывать метод «поиграться» у всех кошачьих, не осознавая разницы.
Вернёмся к нашей практике рисования странных кругов полярных роз. Мы остановились на том, что усложнили работу программы, параллельно создав два массива по 50 объектов разных классов и два таймера с разным периодом срабатывания, у которых практически идентичные обработчики:
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if not Marg then
begin
Petals[CurPetal]:=TPetal.Create(img.Width,img.Height);
Petals[CurPetal].Draw(img.Canvas);
CurPetal+=1;
if CurPetal=50 then Marg:=TRUE;
end else begin
Petals[50-CurPetal].Draw(img.Canvas,TRUE);
Petals[50-CurPetal].Free;
CurPetal-=1;
if CurPetal=0 then Marg:=FALSE;
end;
img.Canvas.TextOut(10,10,IntToStr(CurPetal)+' ');
end;
procedure TForm1.Timer2Timer(Sender: TObject);
begin
if not MargO then
begin
OPetals[CurOPetal]:=TOverlappedPetal.Create(img.Width,img.Height);
OPetals[CurOPetal].Draw(img.Canvas);
CurOPetal+=1;
if CurOPetal=50 then MargO:=TRUE;
end else begin
OPetals[50-CurOPetal].Draw(img.Canvas,TRUE);
OPetals[50-CurOPetal].Free;
CurOPetal-=1;
if CurOPetal=0 then MargO:=FALSE;
end;
img.Canvas.TextOut(50,10,IntToStr(CurOPetal)+' ');
end;
Согласитесь, тру-кодер сам бы сожрал руку, написавшую такой код «с запашком». Раз уж мы решили эволюционировать в настоящих программеров, будем решать задачу избавления от повторяющегося кода и облегчения работы программы.
Сейчас у нас есть два класса: TPetal и его потомок TOverlappedPetal. Однако это немного неправильно и сейчас мы исправим ситуацию. Полярная роза с перекрывающимися лепестками и полярная роза с неперекрывающимися лепестками должны быть классами одного уровня, поскольку с точки зрения классовой теории они равнозначны. Поднимаясь на более высокую ступень абстракции, мы понимаем, что следует ввести базовый класс полярной розы, а вот от него уже порождать два вышеназванных. Всё схожее, что было в двух прежних классах, мы переносим в базовый, таким образом, два потомка будут различаться только самым необходимым:
{ TCustomPetal }
TCustomPetal = class
private
R, phi, PetalI: double;
X, Y, K, CX, CY: integer;
Scale, RColor: integer;
public
constructor Create (Xmax, Ymax: integer); virtual;
procedure Draw (Canvas: TCanvas; Erase: boolean = FALSE);
end;
{ TPetal }
TPetal = class (TCustomPetal)
public
constructor Create (Xmax, Ymax: integer); override;
end;
{ TOverlappedPetal }
TOverlappedPetal = class (TCustomPetal)
public
constructor Create (Xmax, Ymax: integer); override;
end;
Полиморфизм выражен в том, что в реализации потомков перекрывается конструктор базового класса (по миру ходит легенда, что в древних версиях объектного паскаля нельзя было перекрывать конструкторы классов, но я в это не верю). Данный прием реализуется с помощью использования зарезервированных директив virtual и override. Объявляя метод create базового класса виртуальным, мы тем самым даём понять, что реализация конструктора может быть (но не обязательно) перекрыта в потомках. Если бы мы добавили (что в нашем случае вполне возможно, но это усложнит код) к директиве virtual директиву abstract, то это бы значило, что реализации конструктора в базовом классе не будет, но потомки обязаны иметь такую реализацию. Мы не станем делать конструктор базового класса абстрактным, поскольку его реализация имеет и общие черты для потомков:
constructor TCustomPetal.Create(Xmax, Ymax: integer);
begin
inherited Create;
CX:=Random(Xmax);
CY:=Random(Ymax);
RColor:=1+Random($FFFFF0);
Scale:=2+Random(12);
end;
constructor TOverlappedPetal.Create(Xmax, Ymax: integer);
begin
inherited Create (Xmax,Ymax);
K:=12;
while PetalI=Round(PetalI) do
PetalI:=(1+Random(6))/(1+Random(6));
end;
constructor TPetal.Create(Xmax, Ymax: integer);
begin
inherited Create (Xmax,Ymax);
K:=2;
PetalI:=1+Random(8);
end;
Итак, конструктор базового класса осуществляет инициализацию общих для потомков полей — координаты центра, цвет и масштаб. А вот конструкторы потомков сперва вызывают конструктор базового класса, а потом осуществляют разную инициализацию оставшихся полей — коэффициент для угловой координаты и коэффициент, определяющий форму полярной розы.
Теперь посмотрите, как упрощается основной код программы. Вместо двух массивов с пятидесятью объектов разных классов мы объявляем один массив с объектами класса TCustomPetal, а обработчик события в таймере переписываем следующим образом:
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if not Marg then
begin
if Random(2)=1 then Petals[CurPetal]:=TPetal.Create(img.Width,img.Height)
else Petals[CurPetal]:=TOverlappedPetal.Create(img.Width,img.Height);
Petals[CurPetal].Draw(img.Canvas);
CurPetal+=1;
if CurPetal=50 then Marg:=TRUE;
end else begin
Petals[50-CurPetal].Draw(img.Canvas,TRUE);
Petals[50-CurPetal].Free;
CurPetal-=1;
if CurPetal=0 then Marg:=FALSE;
end;
img.Canvas.TextOut(10,10,IntToStr(CurPetal)+' ');
end;
Логика работы: берется случайное число от 0 до 3 и если оно равно 1, то для очередного объекта из массива CustomPetal вызывается конструктор класса-потомка TPetal, в противном случае вызывается конструктор класса-потомка TOverlappedPetal. В этом и проявляется полиморфизм: не смотря на то, что массив объектов у нас одного и того же типа TCustomPetal, по факту объекты создаются с типом потомка. Поскольку у них одни и те же поля, одни и те же методы — работа с ними ничем не отличается для программы. Мы вызываем одинаковый метод DrawPetal, но ведет он себя по-разному в зависимости от типа объекта. Согласитесь, код программы заметно упростился и стал более наглядным (для тех, кто все-таки вкурил парадигму ООП).
Свежий пример с изменениями — в ветке lersson3.
Как еще можно усовершенствовать работу? На мой вкус более симпатичным является вариант, где 50 роз не последовательно рисуются и затираются, а когда это происходит непрерывно. Для этого следует немного изменить обработчик таймера, это уже не связано с ООП, но заставляет пошевелить мозгами:
procedure TForm1.Timer1Timer(Sender: TObject);
begin
if Assigned (Petals[CurPetal]) then
begin
Petals[CurPetal].Draw(img.Canvas,TRUE);
Petals[CurPetal].Free;
end;
if Random(2)=1 then Petals[CurPetal]:=TPetal.Create(img.Width,img.Height)
else Petals[CurPetal]:=TOverlappedPetal.Create(img.Width,img.Height);
Petals[CurPetal].Draw(img.Canvas);
CurPetal+=1;
if CurPetal=PetalC then CurPetal:=0;
img.Canvas.TextOut(10,10,IntToStr(CurPetal)+' ');
end;
В целях еще большего совершенствования программы, я сделал массив роз динамическим (Petals: array of TCustomPetal), а в обработчике события при создании формы ему устанавливается размер — увеличил до 70, поскольку 50 роз на экране выглядят слишком жиденько. Логика работы обработчика таймера изменилась и вместе с тем упростилась: CurPetal — это наш указатель на текущий номер розы в массиве, и он пробегает бесконечно от 0 до 70 (т.к. динамические массивы всегда начинают нумерацию с нуля). Сначала проверяется, создан ли ранее элемент массива роз с номером CurPetal, и если да, то он затирается и уничтожается. Затем случайным способом создается тот же элемент с тем же номером. Указатель на номер массива инкременируется, и если он становится больше границы массива, то обнуляется (в нашем случае, последним существующим элементом массива будет элемент с номером 69, т.к. нумерация, напомню, идет с нуля). Окончательный вид скринсейвера (вверху для наглядности — счетчик):
Итоговый проект — в ветке lesson3-1.
В самом последнем варианте объем используемой во время работы памяти компьютера сократился до 7 с небольшим Мб, тогда как в начале приложение во всю веселилось с 30 Мб. Использование ООП, рефакторинг кода и знание математики позволяют делать красивый и эффективный код, помните это всегда.
Автор: java73





