Сказать, что Petrify решает, поставленные перед ней задачи, можно лишь с большой натяжкой. Вернее она кое-что может для небольших заданий (где количество сигналов едва превышает 20), проблема взрыва состояний так и не была решена. Но и для таких задач удовлетворительный результат не гарантирован. Декомпозиция далеко не всегда дает приемлемые результаты.
В чем причина этих неудач? Я бы назвал 3 основные:
1. Увлеченность STG. Да, это красивая, забавная модель, очень интересно играть маркерами и т.п. Но, подумайте, процесс переключения сигналов схемы это такой же процесс как выполнение какой-либо программы. Мы используем для описания программы сети Петри? Для чего тогда они нужны при описании процессов, происходящих в схеме? В результате разработчики Petrify львиную долю своих усилий потратили на изучение свойств сетей Петри. А собственно задачи синтеза схем так и не были решены.
2. Упор на «вычислительность». Под этим я подразумеваю убежденность, что для синтеза схем обязательно нужно вычислять логические функции. Как результат, вместо решения задач синтеза, исследовались только возможности уменьшения таких вычислений.
3. Неспособность разобраться в причинах возникающих проблем. Но об этом ниже.
А есть ли в Petrify, что-либо хорошее? Да, есть! Это — ДЕКОМПОЗИЦИЯ. На самом деле это естественный, фундаментальный и прекраснейший метод. Важно только разобраться в причинах, почему обычно невозможна декомпозиция до минимальных двухвходовых элементов без нарушения спид-индепендед. А причина этого — кратные сигналы. Под этим я подразумеваю сигналы, которые переключаются более чем 2 раза за цикл, или же сигналы переключающиеся в двух и более альтернативных ветвях. Авторами Petrify этот факт установлен не был, чему свидетельство «жадный» алгоритм добавления дополнительных сигналов. При этом количество дополнительных сигналов уменьшается за счет увеличения числа переключений таких сигналов. Да, это уменьшает объем вычислений (которые, как я покажу ниже вообще не нужны), но создает дополнительные проблемы для декомпозиции.
Покажу на примере что я имею ввиду. Рассмотрим поведение со следующими ограничениями:
1. нет выбора;
2. нет параллелизма;
3. нет входных сигналов;
4. поведение знакочередуемое, за "+" следует "-", за "-" — "+";
5. все сигналы переключаются строго по 2 раза.
Устранение CSC противоречий, даже с сохранением выше перечисленных ограничений, ни у кого вызывать проблем не должно. Теперь каждый сигнал представим в виде триггера:
было:
$$display$$ ... x+ ... x- ... $$display$$
стало:
$$display$$ ... y- x+ ... x- y+ ... $$display$$
После этого уравнение в общем виде для каждого сигнала выглядит так:
$$display$$x=NOR(y,AND(a,b,c,...,d)) $$display$$
Поведение сигналов этого уравнения выглядит так:
$$display$$... d- ... y- x+ ... c- ... d+ ... b- ... c+ ... a- ... b+ ... a+ x- y+ ... $$display$$
Вычислять такое уравнение нет необходимости. Нужно на графе найти цепочку подхватов a, b, c, d (против часовой стрелки) от x-, перескакивающую через x+. CSC свойство это обеспечивает.
А теперь сделаем декомпозицию этого уравнения:
$inline$x=NOR(y,f) $inline$
$inline$f=AND(g,a) $inline$
$inline$g=AND(h,b) $inline$
$inline$h=AND(c,d) $inline$
Поведение будет выглядеть так:
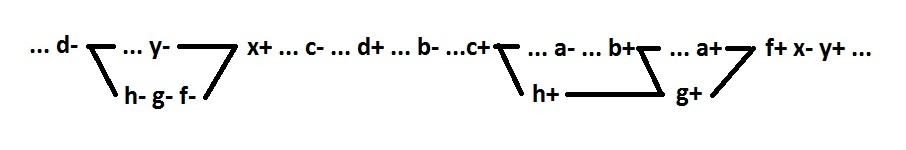
Как видно таким образом можно синтезировать спид-индепендент схему на двухвходовых элементах. Кажется что представление каждого сигнала в виде триггера выглядит громоздко, но далеко не для каждого сигнала в этом есть необходимость. Возникающие при этом нарушения знакочередуемости решаются очень легко, что я покажу ниже.
Итак, мы можем синтезировать схему на двухвходовых элементах для любого поведения, удовлетворяющего 5 выше перечисленным ограничениям. Начнем эти ограничения постепенно снимать.
Снимем ограничение 4 — требование знакочередуемости. В получающейся итоговой схеме все двухвходовые элементы имеют два вида поведения:
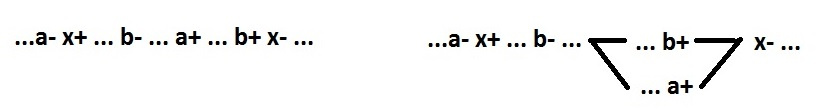
Отмена ограничения 4 может создать только одну проблему: рассогласованность направления переключений между сигналами a и b. Это исправляется введением инвертора (сигнал c). Опять же без нарушения спид-индепендед.
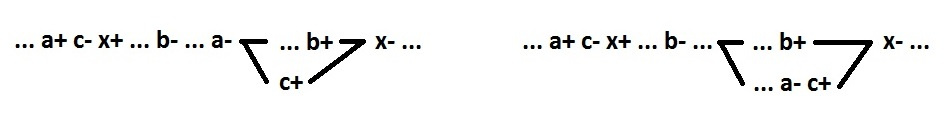
В связи с этим знаки можно расставить в самом конце процесса синтеза схемы (с целью минимизации количества дополнительных инверторов).
Снимем ограничение 3, введем входные сигналы. Так как переключение дополнительного сигнала делать причиной переключения входного сигнала плохая практика, мы это запретим. Всвязи с этим могут возникнуть проблемы, признаком которых является ситуация, когда переключение входного сигнала является причиной переключения входного сигнала. Всего выделяются 3 класса проблемных поведений.
1 класс. В упрощенном виде это переключение входного сигнала дважды подряд:
$$display$$... n+ n- ... $$display$$
В этом случае приходится вставлять дополнительные события перед входным. Иначе схему вообще нельзя построить. Делается это самым щадящим образом. Исправляется так:
$$display$$... n+ a- b+ n- c+ ... d+ b- a+ c- ... d- ... $$display$$
При этом:
$inline$a=NOR(n,b) $inline$
$inline$b=NOR(d,a) $inline$
$inline$c=NOR(a,n) $inline$
Сигналы a, b, c объявляются псевдовходными, т.е. вводится запрет на вставку дополнительных событий перед ними. Далее можно работать с поведением как описано выше, при этом сигнал n вообще можно вывести из рассмотрения.
2 класс — выбор в зависимости от порядка переключения двух входных сигналов:
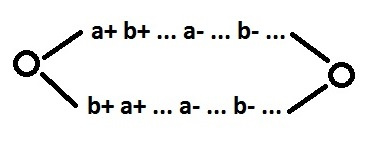
Здесь я забегаю вперед, поскольку ограничение на использование выбора еще не снято. Смысл коррекции в том, чтобы получить поведение с простым выбором, в зависимости от того, какой из двух псевдовходных сигналов переключится (h или g).
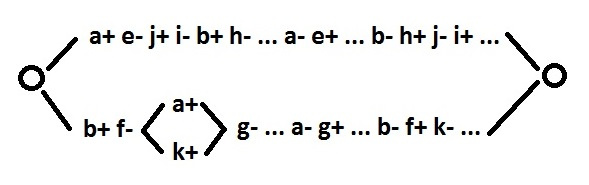
$inline$e=NAND(a,f) $inline$
$inline$j=NAND(e,h) $inline$
$inline$i=NOT(j) $inline$
$inline$h=NAND(b,j) $inline$
$inline$f=NAND(b,i) $inline$
$inline$k=NOT(f) $inline$
$inline$g=NAND(a,k) $inline$
Сигналы e, j, i, h, f, k, g объявляются псевдовходными. Сигналы a, b можно убрать из рассмотрения. Более сложная коррекция в верхней ветви обусловлена порядком переключений a- и b-. Если в верхней ветви их поменять местами, то решение будет такое же как в нижней ветви.
3 класс — выбор по уровню. Выбор делается в момент переключения входного сигнала a+ в зависимости от значения входного сигнала b, установившегося к этому моменту.
Цель коррекции такая же, как в предыдущем случае.
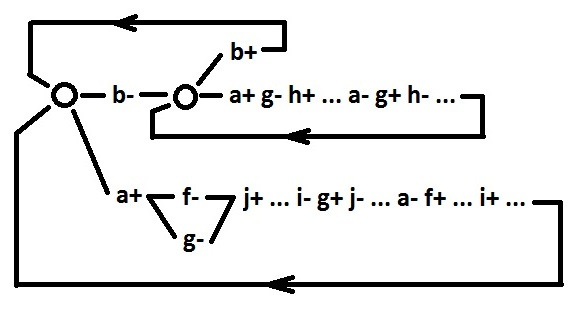
$inline$g=NAND(a,i) $inline$
$inline$h=NOR(b,g) $inline$
$inline$f=NAND(a,b) $inline$
$inline$j=NOR(f,g) $inline$
Сигналы g, h, f, j объявляются псевдовходными. Сигналы a, b, g далее можно не рассматривать. Выбор теперь определяется событиями h+ и j+. Как видно здесь даже нет нарушения спид-индепендент.
Теперь снимем ограничение 5, введем кратные сигналы.
$$display$$... x- ... x+ ... x- ... x+ ... $$display$$
Для нейтрализации кратного сигнала x введем дополнительные сигналы.
$$display$$... a+ x- b+ ... a- x+ b- ... c+ d- ... f+ x- g+ ... f- x+ g- ... c- d+ ... $$display$$
$inline$x=NOR(a,f) $inline$
$inline$b=NOR(x,c) $inline$
$inline$g=NOR(x,d) $inline$
Сигналы x, b, g объявляются псевдовходными. Сигнал x дальше может не рассматриваться.
Отменим ограничение 2, введем параллелизм. С параллелизмом связаны следующие проблемы.
1. Нужно обеспечить синхронизацию параллельных ветвей.
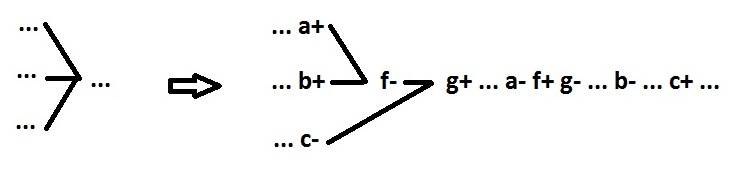
$inline$f=NAND(a,b) $inline$
$inline$g=NOR(f,c) $inline$
Сигналы f, g объявляются псевдовходными.
2. Событие a+ не может быть причиной события b-, если события a- и b+ параллельны.
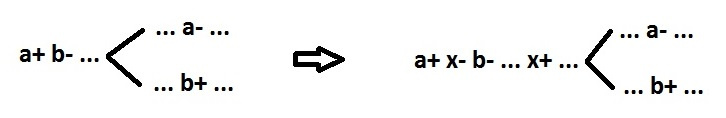
Кроме вышеперечисленных проблем параллелизм не препятствует декомпозиции.
Наконец, отменим ограничение 1, введем выбор.
Для удобства будем рассматривать поведение без параллелизма. А выбор осуществляется в зависимости от переключения одного из двух входных сигналов. Поведение будем представлять в виде ориентированного графа, где вершины — точки выбора, дуги — последовательные переключения сигналов. В каждой вершине ровно по две выходные дуги.
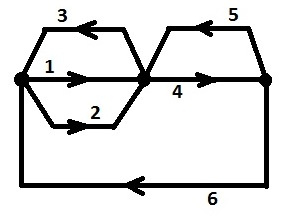
Метод синтеза состоит в последовательном дроблении исходного поведения с выбором до получения нескольких отдельных поведений без выбора.
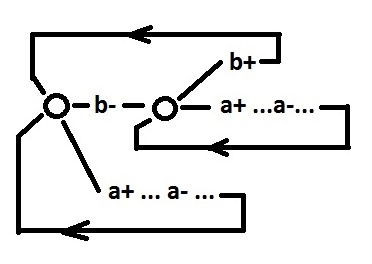
Определим понятие: множество достижимых дуг из дуги N. Это все дуги через которые проходят все возможные пути из дуги N. При этом точка выбора, из которой выходит дуга N, является последней для каждого пути.
Например: для дуги 4 множество достижимых дуг — {4, 5, 6, 1, 2}. Для дуги 3 — {3, 1, 2}. Алгоритм синтеза таков. Для каждой точки выбора, для обеих ее выходных дуг ищем множества достижимых дуг.
1. Если найдется точка выбора, для которой множества достижимых дуг не пересекаются. По этой точке можно разделить поведение на отдельные части. Для этого изолируем сигналы, которые переключаются в обоих частях.
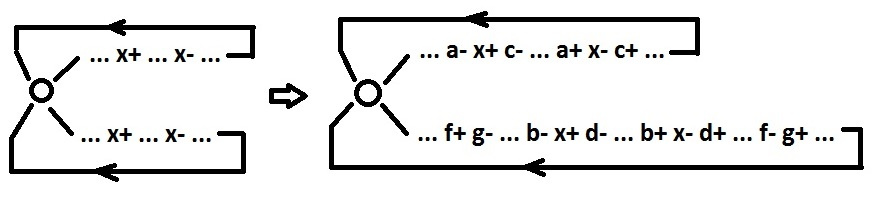
$inline$x=NAND(a,b) $inline$
$inline$c=NAND(x,g) $inline$
$inline$d=NAND(x,f) $inline$
Сигналы x, c, d теперь псевдовходные. Сигнал x далее не рассматриваем. Теперь в обоих частях нет общих сигналов. Взаимодействие между частями осуществляется с помощью входных и псевдовходных сигналов. Каждую такую часть можно рассматривать как отдельное поведение. При этом количество точек выбора по сравнению с исходным поведением уменьшилось как минимум на 1.
2. Если для всех точек выбора множества достижимых дуг пересекаются, но найдется точка выбора, где эти множества не совпадают. По этой точке поведение можно разделить на две части, но более сложным образом.
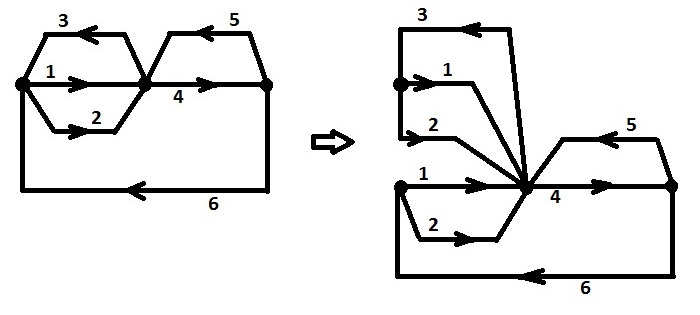
Разделение проходит по точке выбора с выходными дугами 4 и 3. В остальном все тоже: изоляция общих сигналов и разделение на два отдельных поведения с меньшим количеством точек выбора.
3. Если для всех точек выбора множества достижимых дуг совпадают. Берем любую дугу и изолируем все сигналы которые переключаются в ней нечетное число раз.
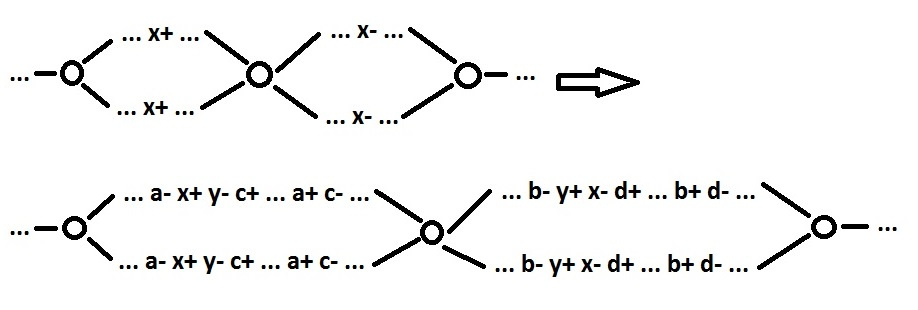
$inline$x= NAND(a,y) $inline$
$inline$y=NAND(b,x) $inline$
$inline$c=NOR(a,y) $inline$
$inline$d=NOR(b,x) $inline$
Сигналы x, y, c, d теперь псевдовходные. После этого изолируем кратные сигналы. В выбранной дуге остались только сигналы, которые переключаются только в этой дуге (по два раза). Такую дугу можно рассматривать как полноценное циклическое поведение. Из исходного поведения эта дуга изымается, так что количество точек выбора уменьшается на 1.
Таким образом поведение с выбором постепенно дробится до поведений без выбора.
Описанный выше метод не является искусственным, придуманным. Хотя синтез схем на двухвходовых элементах кажется экстремальным, на самом деле он прост в том смысле, что до предела сужает пространство возможных решений. Например, изоляция кратных сигналов нужна не для декомпозиции, и не для дробления поведений с выбором. Изоляция нужна сама по себе. Без нее невозможно встроить кратные сигналы в двухвходовую схему. А уж если приходится делать изоляцию, то совершенно бессмысленно отказываться от декомпозиции и от дробления поведений с выбором.
Все описанные проблемы присущи и синтезу в произвольной элементной базе. Только решение этих проблем обычно носит случайный, не явный характер. И как следствие этого они избыточны. К примеру, я сравнивал свои решения с бенчмарками Petrify. Мои решения в 1.5 раза меньше. И это при том, что Petrify позволяет себе такие вольности, как использование нестандартных элементов (C-элемент), использование элементов с двухуровневой логикой, гораздо меньшее ограничение по количеству входов элемента, ограничения по задержкам при использовании входных инверторов.
Автор: ajrec