
Математики из Ливерпульского университета в своей новой работе опубликовали несколько неизвестных ранее способов разбиения диска на равные части. Эта работа принадлежит к разделу геометрии, изучающему т.н. паркеты — замощение плоскости многоугольниками без пробелов и перекрытий. На работу учёных вдохновили поиски способов резки пиццы – знакомой большинству из нас процедуры.
При замощении плоскости геометрическими фигурами (плитками) можно ставить и решать разные задачи. Одна из самых интересных задач – использование моноэдрических плиток. В этом случае все плитки имеют одну и ту же форму, или, точнее говоря, конгруэнтны. Это значит, что две любые плитки можно совместить при помощи перемещений, поворотов или зеркального отражения.
Набор форм плиток, используемых для замещения плоскости, называют протоплитками. Интересно, что не существует математического метода, позволяющего заранее сказать, можно ли при помощи заданных протоплиток заместить плоскость. Например, известно, что из следующих 24 гептамондов (фигур, составленных из семи равносторонних треугольников) лишь один непригоден для моноэдрического замощения плоскости. Но какой именно?

В данном случае – V-образный. Но доказательство этого – задача довольно нетривиальная.
Впрочем, ливерпульские математики вместо целой плоскости ограничились диском и занялись поисками моноэдрических протоплиток, подходящих для деления диска. Один вариант такой протоплитки известен всем. При стандартном способе резки пиццы она делится на равные дольки треугольной формы, вершины которых сходятся в центре диска. Учёные же решили ответить на вопрос – существуют ли такие деления диска на равные фигуры, при которых не все из этих фигур касаются центра диска?
То есть, можно ли разрезать пиццу на равные части так, чтобы угодить и тем, кто любит побольше начинки, и тем, кто любит побольше корочки? Оказалось, что можно. Более того, один вариант такой резки известен достаточно давно, и расположен на логотипе сообщества Университета штата Пенсильвания, организовывающего математические семинары для студентов:
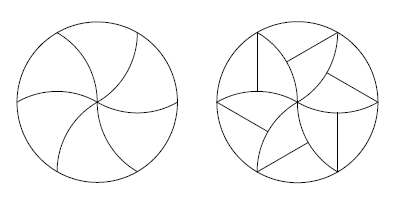
Фигурные дольки можно поделить пополам, и все части получатся конгруэнтными, при этом лишь половина из них будет касаться центра.
Математики развили эту идею и предложили свои способы деления диска на практически бесконечное количество равных частей.
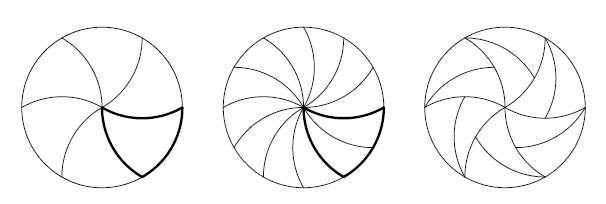

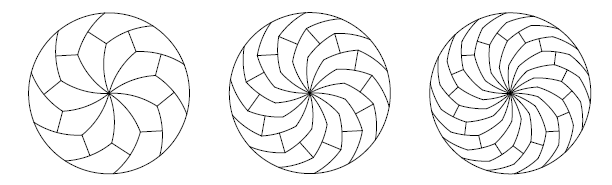
Как это часто бывает в математике, возможности применения идей работы на практике не совсем очевидны – разве что, использование пиццерией нестандартной резки пиццы в качестве конкурентного преимущества. Но с другой стороны, предсказать, каким образом математическое открытие сможет пригодиться в будущем, тоже невозможно.
Автор: SLY_G








