Всем привет! Когда-то давным-давно я делал простенькие игрушки на Flash. Например: игрушка — провести курсор мышки через лабиринт, не касаясь стен и уворачиваясь от всяких движущихся объектов. Некоторые из этих объектов двигаются по заданной траектории, некоторые гонятся за курсором, а некоторые стреляют в курсор другими движущимися объектами.
Сейчас я увлёкся программированием под андроид и сделал примерно такую же игрушку. И столкнулся с теми же геометрическими задачками с которыми встречался тогда.
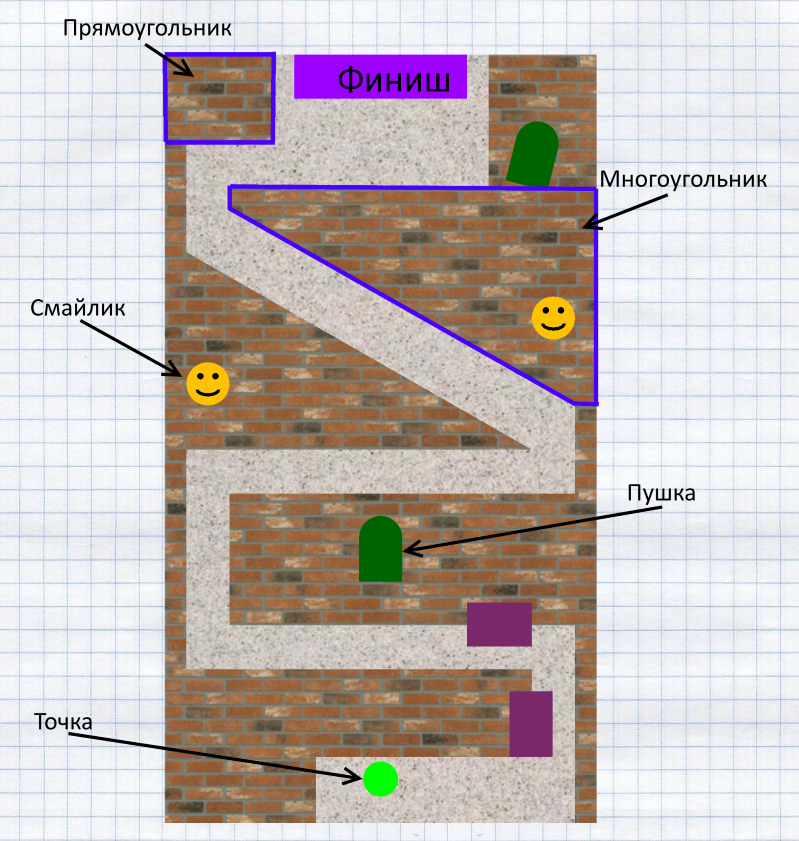
Задачка 1: нарисовать стены. И сразу возникает Задачка 2: определить касается ли точка стены или нет (проиграл ты или продолжать игру).
Для этого я поделил стены на фигуры: прямоугольники и многоугольники.
С прямоугольниками всё просто: Просто нарисовать:
canvas.drawRect(x1, y1, x2, y2, paint);и просто проверить находится ли точка внутри него или нет.
public boolean isTouched(float x, float y){
return (x>x1)&&(x<x2)&&(y>y1)&&(y<y2);
}С многоугольником дело обстоит не так просто: нарисовать его уже немного сложнее.
Path path = new Path();
paint.setStyle(Paint.Style.FILL);
path.moveTo(x1, y1);
path.lineTo(x2, y2);
path.lineTo(x3, y3);
.....
path.lineTo(x1, y1); //замыкаем фигуру
path.close();
canvas.drawPath(path, paint);А проверить касание с точкой ещё сложнее. Я попытался вспомнить школьный курс геометрии, потом погуглил и нашёл такое решение:
Многоугольник обязательно должен быть выпуклым.
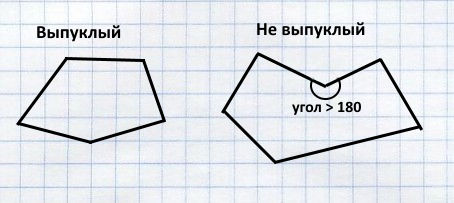
И описывать его надо обязательно по часовой стрелке.
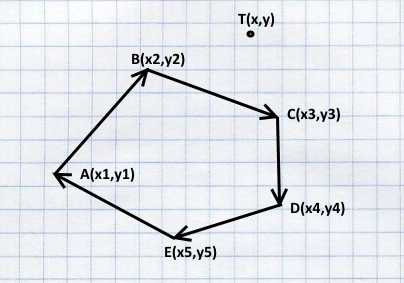
При этом каждое ребро имеет начальные и конечные координаты, то есть по сути является вектором. И можно определить находится ли точка справа или слева от него.
Для этого есть простая формула.
private boolean isLeftHandSituated(float dotX, float dotY, float x1, float y1, float x2, float y2){
float d = (dotX - x1) * (y2 - y1) - (dotY - y1) * (x2 - x1);
return d>0;
}Чтобы определить внутри ли точка или снаружи я в цикле перебираю все рёбра, и если хоть для одного ребра точка находится слева (в данном случае это ребро BC) — значит она снаружи, так как многогранник описан по часовой стрелке.
Задачка 3: жёлтый смайлик. Если точка приближается к нему на определённое расстояние, то он гонится за точкой. Вычислить это определённое расстояние (distance) можно по теореме Пифагора:
float dx = dotX - smileX;
float dy = dotY - smileY;
double distance = Math.sqrt((dx * dx + dy * dy));Смайлик гонится за точкой. Что это значит? Это значит что через каждый определённый интервал времени (в следующем кадре) его координаты перемещаются на определённое расстояние ближе к точке. Это расстояние за кадр по сути является скоростью. Я назвал переменную speed.
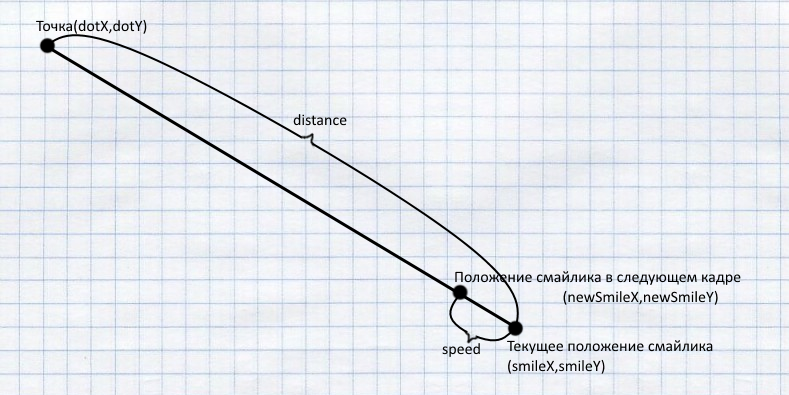
Вычислить координаты смайлика в следующем кадре можно так:
private float speed=5;
double rate = speed / distance;
newSmileX = smileX + (float) (dx * rate);
newSmileY = smileY + (float) (dy * rate);Задачка 4: пушка всё время направлена на точку. Как вычислить угол на который её надо повернуть? Очень просто. Для этого существует метод atan2.
float dx = dotX - cannonX;
float dy = dotY - cannonY;
double theta = Math.atan2(dx, dy); //получаем угол в радианах
angle = Math.toDegrees(theta); //переводим его в градусы.Заключение: Статья получилась довольно сжатая и короткая, но, надеюсь, полезная многим начинающим разработчикам игр. Всем удачи в обучении и разработке!
Автор: Andrey_139








