
В мире математики сенсация. Открыт новый вид пятиугольников, которые покрывают плоскость без разрывов и без перекрытий.
Это всего 15-й вид таких пятиугольников и первый, открытый за последние 30 лет.
Плоскость покрывается треугольниками и четырехугольниками любой формы, а вот с пятиугольниками все гораздо сложнее и интереснее. Правильные пятиугольники не могут покрыть плоскость, но некоторые неправильные пятиугольники могут. Поиск таких фигур уже сто лет является одной из самых интересных математических задач. Квест начался в 1918 году, когда математик Карл Рейнхард открыл пять первых подходящих фигур.
Долгое время считалось, что Рейнхард рассчитал все возможные формулы и больше таких пятиугольников не существует, но в 1968 году математик Р.Б.Кершнер (R. B. Kershner) нашел еще три, а Ричард Джеймс (Richard James) в 1975 году довел их число до девяти. В том же году 50-летняя американская домохозяйка и любительница математики Марджори Райс (Marjorie Rice) разработала собственный метод нотации и в течение нескольких лет открыла еще четыре пятиугольника. Наконец, в 1985 году Рольф Штайн довел число фигур до четырнадцати.
Пятиугольники остаются единственной фигурой, в отношении которой сохраняется неопределенность и загадка. В 1963 году было доказано, что существует всего три вида шестиугольников, покрывающих плоскость. Среди выпуклых семи-, восьми- и так далее -угольников таких нет. А вот с «пентагонами» пока не все ясно до конца.
До сегодняшнего дня было известно всего 14 видов таких пятиугольников. Они изображены на иллюстрации. Формулы для каждого из них приведены по ссылке.

В течение 30 лет никто не мог найти ничего нового, и вот наконец-то долгожданное открытие! Его сделала группа ученых из Вашингтонского университета: Кейси Манн (Casey Mann), Дженнифер Маклауд (Jennifer McLoud) и Дэвид вон Деро (David Von Derau). Вот как выглядит маленький красавчик.
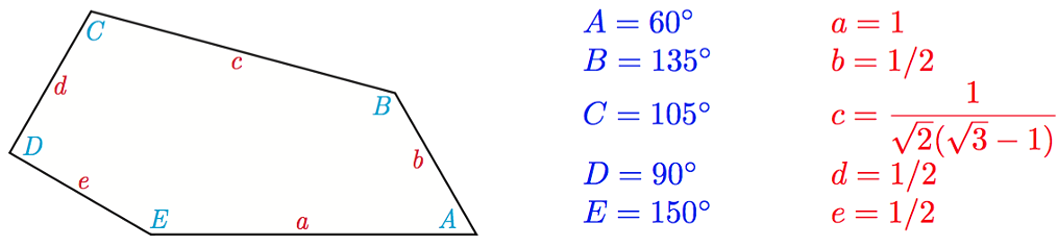
«Мы открыли фигуру с помощью компьютерного перебора большого, но ограниченного количества вариантов, — говорит Кейси Манн. — Конечно, мы очень взволнованы и немного удивлены, что удалось открыть новый вид пятиугольника».
Открытие кажется чисто абстрактным, но на самом деле оно может найти практическое применение. Например, в производстве отделочной плитки.

Поиск новых пятиугольников, покрывающих плоскость, наверняка продолжится.
Автор: alizar









Я активно занимаюсь определением фактора пи для плоских и объёмных фигур. Например для правильного треугольника П = 3 х 3^0,5 = 5,196152423 = 27^0,5 Для квадрата П = 4. Для куба П=6. Для правильного шестиугольника П = 2 х 3^0,5 = 3,464101515 = 12^0,5. Для египетских треугольников с отношением сторон 3:4:5, П = 6, для соотношения сторон 5:12:13, П = 7,5. и т.д. и т. п. Всё это описано на сайте http://www.senezh.org/
Фактор пи рассчитывается по формуле П = (L^2) : F. Где L- полупериметр, F – площадь ограниченная периметром. Мы можем засвидетельствовать вашу работу на сайте как авторскую. Это имеет большое значение для нового вида деятельности под названием ИНВАРИАНТНОЕ ПРОЕКТИРОВАНИЕ.