Решение японских кроссвордов на Haskell

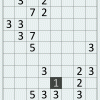
Японский кроссворд — головоломка, в которой по набору чисел нужно воссоздать исходное черно-белое изображение. Каждой строке и каждому столбцу пикселей соответствует свой набор, каждое число в котором, в свою очередь, соответствует длине блока подряд идущих черных пикселей. Между такими блоками должен быть хотя бы один белый пиксель, но точное их число неизвестно. Журналы, целиком посвященные этим головоломкам, есть в большинстве газетных киосков, так что, думаю, почти все с ними хоть раз да встречались, и потому более подробное описание здесь можно не приводить.

В какой-то момент мне захотелось «научить компьютер» решать японские кроссворды так, как решаю их я сам. Никакой высокой цели, just for fun. Потом уже были добавлены способы, которые сам я применять не могу в силу ограниченных возможностей человеческого мозга, но, справедливости ради, со всеми кроссвордами из журналов программа справляется и без них.

Итак, задача простая: решить кроссворд, а если решений много, то найти их все. Решение написано на Haskell'е, и, хотя код достаточно существенно дополняет словесное описание, даже без знания языка общую суть понять можно. Если хочется пощупать результат вживую, на странице пректа можно скачать исходники (бинарных сборок не выкладывал). Решения экспортируются в Binary PBM, из него же можно извлекать условия.

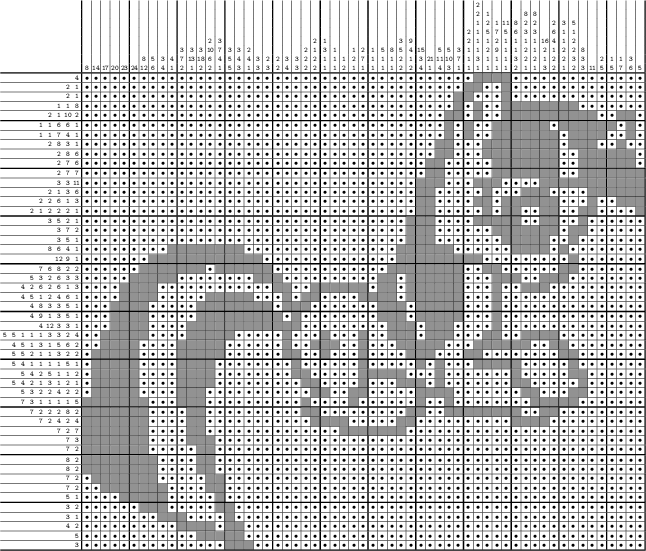
Несмотря на то, что я пытался писать максимально понятно, это не в полной мере мне удалось. Под катом очень много букв и кода и почти нет картинок.

BitMask

В основе всей программы лежит свой велосипед для битовой маски. Он не слишком быстр, но обладает свойством, которое было для меня важно в процессе отладки: падает при операциях, не имеющих смысла, а именно при любой операции над масками разной длины. Я приведу здесь лишь сигнатуры функций и картинку, поясняющую принцип их работы; реализация весьма примитивна и непосредственно к решению отношения не имеет.

bmCreate         :: Int       -> BitMask
bmLength         :: BitMask   -> Int
bmSize           :: BitMask   -> Int
bmIsEmpty        :: BitMask   -> Bool
bmNot            :: BitMask   -> BitMask
bmAnd            :: BitMask   -> BitMask   -> BitMask
bmOr             :: BitMask   -> BitMask   -> BitMask
bmIntersection   :: [BitMask] -> BitMask
bmUnion          :: [BitMask] -> BitMask
bmSplit          :: BitMask   -> [BitMask]
bmByOne          :: BitMask   -> [BitMask]
bmExpand         :: BitMask   -> BitMask
bmFillGaps       :: BitMask   -> BitMask
bmLeftIncursion  :: Int       -> BitMask   -> BitMask
bmRightIncursion :: Int       -> BitMask   -> BitMask
bmTranspose      :: [BitMask] -> [BitMask]

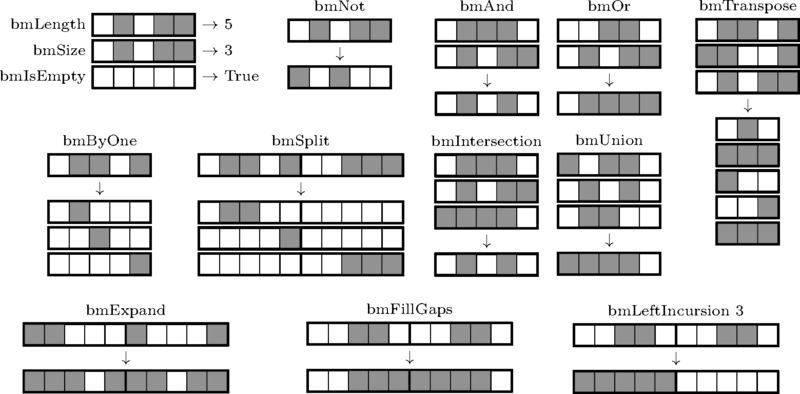
Думаю, что такое графическое описание исчерпывающе для всех функций, кроме, пожалуй, bmLeftIncursion и bmRightIncursion. Зачем они нужны, будет ясно позже, принцип же их работы следующий: bmLeftIncursion находит самый левый заполненный бит и создает маску, в которой заполнены все биты до него, а также столько бит начиная с него, сколько было указано при вызове функции; вторая функция работает аналогично.

Структура

Так как решение кроссворда происходит по линиям, то тип, соответствующий всему полю, представляет собой набор всех горизонтальных и вертикальных линий, хоть это и приводит к дублированию всех клеток кроссворда.

data Field = Field {
    flHorLines :: [Line],
    flVerLines :: [Line]
    } deriving Eq

Каждая линия хранит информацию о клетках и блоках (блок соответствует числу в условии).

data Line = Line {
    lnMask :: LineMask,
    lnBlocks :: [Block]
    } deriving Eq

Информация о клетках хранится в виде двух битовых масок одинаковой длины, представляющих закрашенные и заблокированные клетки.

data LineMask = LineMask {
    lmFilledMask :: BitMask,
    lmBlockedMask :: BitMask
    } deriving Eq

Блок же, помимо непосредственно числа, содержит маску, которая соответствует той области линии, в которой данный блок может находиться.

data Block = Block {
    blScopeMask :: BitMask,
    blNumber :: Int
    } deriving Eq

В начале решения маски закрашенных и заблокированных клеток пусты, а маска блока, наоборот, полностью заполнена. Это значит, что все клетки пусты, а каждый блок может находиться в любой части линии. Процесс решения сводится к тому, чтобы сузить область каждого блока до размеров, равных его числу, и соответствующим образом заполнить маски.

Завершенность и синхронизация

Все вышеперечисленные типы (кроме BitMask) являются экземплярами двух классов: Completable и Syncable.

Единственная функция класса Completable показывет «завершенность» объекта. Поле считается завершенным, если завершены все его линии. Линия завершена, если завершены все ее блоки; завершенности маски при этом требовать излишне (она следует из завершенности блоков; почему, опять же, будет ясно чуть позже). Для завершения блока, как уже упоминалось выше, необходимо, чтобы размер его области совпадал с его числом.

class Completable a where
    clIsCompleted :: a -> Bool

instance Completable Field where
    clIsCompleted fl = all clIsCompleted (flHorLines fl) && all clIsCompleted (flVerLines fl)

instance Completable Line where
    clIsCompleted ln = all clIsCompleted (lnBlocks ln)

instance Completable Block where
    clIsCompleted bl = bmSize (blScopeMask bl) == blNumber bl

Класс Syncable предоставляет функции, которые позволяют свести воедино разные ветки решений. snAverage выделяет из двух веток только общее, а snSync — то, что проявилось хотя бы в одной ветке (можно считать их обобщениями функций bmAnd и bmOr соответственно). snAverageAll и snSyncAll делают абсолютно то же самое, но работают не с двумя объектами, а со списками объектов.

class Syncable a where
    snSync :: a -> a -> Maybe a
    sn1 `snSync` sn2 = snSyncAll [sn1, sn2]
    snAverage :: a -> a -> Maybe a
    sn1 `snAverage` sn2 = snAverageAll [sn1, sn2]
    snSyncAll :: [a] -> Maybe a
    snSyncAll [] = Nothing
    snSyncAll sns = foldr1 (wrap snSync) (map return sns)
    snAverageAll :: [a] -> Maybe a
    snAverageAll [] = Nothing
    snAverageAll sns = foldr1 (wrap snAverage) (map return sns)

wrap :: Monad m => (a -> b -> m c) -> m a -> m b -> m c
wrap f mx my = do
    x <- mx
    y <- my
    f x y

Согласованность

Из описания функций класса Syncable видно, что их результатом является объект, обернутый в монаду Maybe. На самом деле, так проявляется важное понятие согласованности, которое тоже определено для всех вышеперечисленных типов, но в отдельный класс не вынесено из соображений инкапсуляции. Как пример, одна и та же клетка не может быть одновременная закрашенной и заблокированной; если какая-либо операция может привести к такой ситуации, то она помечена монадой Maybe (как правило, имеет тип type TransformFunction a = a -> Maybe a), и, если она к этой ситуации приводит, то результатом ее будет Nothing, потому что ни один объект в программе не может существовать в несогласованном состоянии. Так как Nothing, в свою очередь, не может являться составной частью других объектов, несогласованным станет все поле, что будет означать отсутствие решений.

Согласованность поля обеспечивается синхронизацией горизонтальных и вертикальных линий. Таким образом, если клетка находится в каком-то состоянии (закрашена, заблокирована или пуста) в горизонтальной линии, то она находится точно в том же состоянии в соответствующей вертикальной линии, и наоборот.

flEnsureConsistency :: TransformFunction Field
flEnsureConsistency fl = do
    let lnsHor = flHorLines fl
    let lnsVer = flVerLines fl
    lnsHor' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsVer) lnsHor
    lnsVer' <- zipWithM lnSyncWithLineMask (lmTranspose $ map lnMask lnsHor) lnsVer
    return $ Field lnsHor' lnsVer'

lnSyncWithLineMask :: LineMask -> TransformFunction Line
lnSyncWithLineMask lm ln = do
    lm' <- lm `snSync` lnMask ln
    return ln { lnMask = lm' }

О согласованности линии поговорим позже, так как она имеет непосредственное отношение к процессу решения.

Согласованность блока обеспечивается нетривиально: для нее необходимо исключить из области блока те непрерывные части, которые не могут его вместить. Таким образом, если из области блока с числом 3 и исходной областью исключить маску (например, по причине того, что эта клетка оказалась заблокирована), то конечным итогом этой операции будет блок с областью , а вовсе не .

blEnsureConsistency :: TransformFunction Block
blEnsureConsistency bl = do
    let bms = filter ((blNumber bl <=) . bmSize) $ bmSplit $ blScopeMask bl
    guard $ not $ null bms
    return bl { blScopeMask = bmUnion bms }

Для маски согласованность очевидна и уже описывалась выше: нельзя одновременно закрасить и заблокировать одну и ту же клетку.

lmEnsureConsistency :: TransformFunction LineMask
lmEnsureConsistency lm = do
    guard $ bmIsEmpty $ lmFilledMask lm `bmAnd` lmBlockedMask lm
    return lm

Преобразования

Операции преобразования масок и блоков весьма ограничены, так как в процессе решения клетки можно только закрашивать и блокировать (передумать, взять ластик и стереть уже нельзя), а область блока можно лишь сужать.

lmFill :: BitMask -> TransformFunction LineMask
lmFill bm lm = lmEnsureConsistency lm { lmFilledMask = lmFilledMask lm `bmOr` bm }

lmBlock :: BitMask -> TransformFunction LineMask
lmBlock bm lm = lmEnsureConsistency lm { lmBlockedMask = lmBlockedMask lm `bmOr` bm }

blExclude :: BitMask -> TransformFunction Block
blExclude bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bmNot bm }

blKeep :: BitMask -> TransformFunction Block
blKeep bm bl = blEnsureConsistency $ bl { blScopeMask = blScopeMask bl `bmAnd` bm }

Решение

Процесс решения будем рассматривать отдельными частями, пока они, наконец, не сложатся в общую картину.

Согласованность линии

Для начала восстановим пробел, оставленный в разделе про согласованность, и объявим, что линия считается согласованной, если ее маска заполнена в соответствии с ее блоками. За этой фразой скрываются два пункта. Во-первых, должны быть заблокированы те клетки, которые не попадают в область ни к одному блоку (если линия не содержит ни одного блока, то, соответственно, таковыми являются все клетки).

lnUpdateBlocked :: [Block] -> TransformFunction LineMask
lnUpdateBlocked [] lm = lmBlock (bmNot $ lmBlockedMask lm) lm
lnUpdateBlocked bls lm = lmBlock (bmNot $ bmUnion $ map blScopeMask bls) lm

Во-вторых, по каждому блоку при помощи функции blToFillMask можно получить маску, которую неоходимо закрасить. Она является пересечением двух масок, получающихся, если «загнать» блок в самую левую и самую правую части своей области.

blMinimumLeftMask :: Block -> BitMask
blMinimumLeftMask bl = bmLeftIncursion (blNumber bl) (blScopeMask bl)

blMinimumRightMask :: Block -> BitMask
blMinimumRightMask bl = bmRightIncursion (blNumber bl) (blScopeMask bl)

blToFillMask :: Block -> BitMask
blToFillMask bl = blMinimumLeftMask bl `bmAnd` blMinimumRightMask bl

lnUpdateFilled :: [Block] -> TransformFunction LineMask
lnUpdateFilled [] = return
lnUpdateFilled bls = lmFill (bmUnion $ map blToFillMask bls)

(Примечание: здесь мы, наконец, использовали функции bmLeftIncursion и bmRightIncursion. Строго говоря, если бы они применялись только для этой цели, то, скорее всего, выглядели бы немного по-другому, а именно не заполняли бы битовую маску до самого первого заполненного бита исходной маски.)

Таким образом, о чем уже упоминалось ранее, условие согласованности для линии гарантирует, что ее маска всегда будет завершена, если завершены все ее блоки.

lnEnsureConsistency :: TransformFunction Line
lnEnsureConsistency ln = do
    let bls = lnBlocks ln
    lm <- lnUpdateBlocked bls >=> lnUpdateFilled bls $ lnMask ln
    return $ ln { lnMask = lm }

Простое преобразование линии

Решение в рамках линии по сути сводится к двум преобразованиям.

Первое преобразование, фактически, является обратным к условию согласованности: оно гарантирует, что блоки будут завершены, если завершена маска. Для этого используется три действия.

1. Все заблокированные клетки должны быть исключены из областей всех блоков.

   lnRemoveBlocked :: LineMask -> TransformFunction [Block]
   lnRemoveBlocked = mapM . blExclude . lmBlockedMask
   

2. Если блок не может вместить какую-либо непрерывную закрашенную часть маски (то есть если она вылезает за область блока или имеет размер, больший, чем его число), то она должна быть исключена из области блока.

   lnRemoveFilled :: LineMask -> TransformFunction [Block]
   lnRemoveFilled lm = mapM ( bl -> foldM f bl $ bmSplit $ lmFilledMask lm) where
       f bl bm = if blCanContainMask bm bl then return bl else blExclude (bmExpand bm) bl
   
   blCanContainMask :: BitMask -> Block -> Bool
   blCanContainMask bm bl =
       let bm' = bmFillGaps bm
       in bmSize bm' <= blNumber bl && bmIsEmpty (bm' `bmAnd` bmNot (blScopeMask bl))
   

3. Из области каждого блока должны быть исключены blMinimumLeftMask его левого соседа и blMinimumRightMask правого соседа (вот тут уже они нужны именно в том виде, в котором описаны выше). Если быть точным, то исключаются эти маски, расширенные на одну клетку, так как между блоками должна быть хотя бы одна пустая клетка.

   lnExcludeNeighbours :: TransformFunction [Block]
   lnExcludeNeighbours bls = sequence $
       scanr1 (flip $ wrap $ blExclude . bmExpand . blMinimumRightMask) $
       scanl1 (wrap $ blExclude . bmExpand . blMinimumLeftMask) $
       map return bls
   

Вместе эти действия образуют следующую функцию (функция slLoop будет описана позже):

lnSimpleTransform :: TransformFunction Line
lnSimpleTransform ln = do
    let lm = lnMask ln
    bls <- lnRemoveBlocked lm >=> slLoop (lnRemoveFilled lm >=> lnExcludeNeighbours) $ lnBlocks ln
    lnEnsureConsistency ln { lnBlocks = bls }

Второе преобразование линии

Если взять самый левый из всех блоков, которые в принципе могут содержать некоторую закрашенную часть маски, то его крайнее правое положение будет ограничено этой самой маской, ведь если он сдвинется еще правее, то эту закрашенную область уже некому будет «отдать». Те же соображения верны и для самого правого из таких блоков.

lnExtremeOwners :: BitMask -> TransformFunction [Block]
lnExtremeOwners bm bls = do
    bls' <- fmap reverse $ maybe (return bls) (f bmLeftIncursion bls) (h bls)
    fmap reverse $ maybe (return bls') (f bmRightIncursion bls') (h bls')
    where
        f g = varyNth ( bl -> blKeep (g (blNumber bl) bm) bl)
        h = findIndex (blCanContainMask bm)

varyNth :: Monad m => (a -> m a) -> [a] -> Int -> m [a]
varyNth f xs idx = do
    let (xs1, x : xs2) = splitAt idx xs
    x' <- f x
    return $ xs1 ++ x' : xs2

Применяя это рассуждение к каждой непрерывной части маски, получаем второе преобразование линии:

lnTransformByExtremeOwners :: TransformFunction Line
lnTransformByExtremeOwners ln = do
    bls <- foldM (flip lnExtremeOwners) (lnBlocks ln) $ bmSplit $ lmFilledMask $ lnMask ln
    lnEnsureConsistency ln { lnBlocks = bls }

Преобразования поля

Поле каких-то особых собственных преобразований не имеет, единственный вариант для него — взять некоторое готовое преобразование и применить его ко всем своим линиям.

flTransformByLines :: TransformFunction Line -> TransformFunction Field 
flTransformByLines f fl = do
    lnsHor <- mapM f (flHorLines fl)
    fl' <- flEnsureConsistency fl { flHorLines = lnsHor }
    lnsVer <- mapM f (flVerLines fl')
    flEnsureConsistency fl' { flVerLines = lnsVer }

Ветвления

Так как решение японских кроссвордов — NP-полная задача, то без ветвлений обойтись не удастся. Ветвление определим функцией типа type ForkFunction a = a -> [[a]], где внутренний список включает в себя взаимоисключающие варианты, а внешний — различные способы эти варианты произвести.

Простейший способ — ветвление по клеткам: каждая пустая клетка порождает один элемент внешнего списка, являющийся в свою очередь списком из двух элементов, в одном из которых эта клетка закрашена, а в другом заблокирована.

lnForkByCells :: ForkFunction Line
lnForkByCells ln = do
    let lm = lnMask ln
    bm <- bmByOne $ lmEmptyMask lm
    return $ do
        lm' <- [fromJust $ lmBlock bm lm, fromJust $ lmFill bm lm]
        maybeToList $ lnEnsureConsistency ln { lnMask = lm' }

flForkByCells :: ForkFunction Field
flForkByCells fl = do
    let lnsHor = flHorLines fl
    let lnsVer = flVerLines fl
    idx <- findIndices (not . clIsCompleted) lnsHor
    let (lns1, ln : lns2) = splitAt idx lnsHor
    lns <- lnForkByCells ln
    return $ do
        ln' <- lns
        maybeToList $ flEnsureConsistency $ Field (lns1 ++ ln' : lns2) lnsVer

Для линии также доступен другой способ ветвления: для каждой непрерывной закрашенной части маски (внешний список) можно рассматривать набор блоков, которые могут ее содержать (внутренний список), как варианты, определяющие ветки.

lnForkByOwners :: ForkFunction Line
lnForkByOwners ln = do
    let bls = lnBlocks ln
    bm <- bmSplit $ lmFilledMask $ lnMask ln
    case findIndices (blCanContainMask bm) bls of
        [_] -> []
        idxs -> return $ do
            idx <- idxs
            maybeToList $ do
                bls' <- varyNth (g bm) bls idx
                lnEnsureConsistency ln { lnBlocks = bls' }
    where g bm bl = blKeep ((bmAnd `on` ($ bm) . ($ blNumber bl)) bmLeftIncursion bmRightIncursion) bl

Обобщенные функции

Большую часть преобразований имеет смысл применять итерационно. При этом можно просто применять преобразование до тех пор, пока оно хоть что-то меняет, а можно (в случае, когда лишнее применение может занять значительное время) предварительно проверять объект на завершенность.

slLoop :: Eq a => TransformFunction a -> TransformFunction a
slLoop f x = do
    x' <- f x
    if x == x' then return x else slLoop f x'

slSmartLoop :: (Completable a, Eq a) => TransformFunction a -> TransformFunction a
slSmartLoop f x
    | clIsCompleted x = return x
    | otherwise = do
        x' <- f x
        if x == x' then return x else slLoop f x'

Результаты ветвления можно обрабатывать независимо от конкретного типа данных и способа ветвления. Для этого, применив некоторый способ ветвления, а затем применив к каждому получившемуся объекту какую-либо трансформацию, по каждому набору взаимоисключающих веток необходимо взять среднее значение, после чего синхронизировать эти усредненные объекты, полученные различными точками ветвления. Не буду описывать подробно, но для этой операции также доступен оптимизированный вариант, связанный с проверкой на завершенность.

slForkAndSyncAll :: (Syncable a) => ForkFunction a -> TransformFunction a -> TransformFunction a
slForkAndSyncAll f g x = do
    xs <- mapM (snAverageAll . mapMaybe g) $ f x
    snSyncAll (x : xs)

slForkAndSmartSync :: (Syncable a, Completable a, Eq a) => ForkFunction a -> TransformFunction a -> TransformFunction a
slForkAndSmartSync f g x = foldr h (return x) (f x) where
    h xs mx = do
        x' <- mx
        if clIsCompleted x' then mx else case mapMaybe (snSync x') xs of
            [] -> Nothing
            xs' -> case filter (/= x') xs' of
                [] -> return x'
                xs'' -> snAverageAll . mapMaybe g $ xs''

Наконец, если уже ничего не помогает, можно уходить в рекурсию. Только таким способом можно получить все решения, если их несколько.

slAllSolutions :: (Completable a) => ForkFunction a -> TransformFunction a -> a -> [a]
slAllSolutions f g x = do
    x' <- maybeToList $ g x
    if clIsCompleted x' then return x' else case f x' of
        (xs : _) -> do
            x'' <- xs
            slAllSolutions f g x''
        [] -> []

Fina venko

Все. Имеющихся инструментов достаточно, чтобы получить решатель в несколько простых шагов.

1. Скомбинируем два преобразования линии.

   lineTransform = slSmartLoop $ lnSimpleTransform >=> lnTransformByExtremeOwners
   

2. Обработаем специфичное для линии ветвление.

   lineTransform' = slForkAndSyncAll lnForkByOwners lineTransform
   

3. Составим из этих двух преобразований преобразование поля.

   fieldTransform = slSmartLoop $ slSmartLoop (flTransformByLines lineTransform) >=> flTransformByLines lineTransform'
   

4. Обработаем результаты ветвления поля по клеткам.

   fieldTransform' = slForkAndSmartSync flForkByCells fieldTransform
   

5. Объединим предыдущие два преобразования.

   fieldTransform'' = slSmartLoop $ fieldTransform >=> fieldTransform'
   

6. И, наконец, добавим рекурсию.

   solve = slAllSolutions flForkByCells fieldTransform''
   

Послесловие

Программа работает довольно быстро на кроссвордах, имеющих единственное решение: примерно из тысячи имеющихся у меня кроссвордов на моем ноутбуке лишь два (включая вынесеный в предисловие) решаются больше минуты, практически все укладываются в 10 секунд, и при этом ни один не потребовал рекурсии.

Теоретически, при некоторой доработке программу можно использовать для автоматической оценки сложности кроссвордов (так как методы решения в целом аналогичны применяемым человеком) и доказательства единственности решения; экспорт в LaTeX имеется, и даже, возможно, скоро появится в SVN'е. Так что при желании можно организовать домашний выпуск журналов :)

Автор: bodhisattva