Как создаются изометрические миры

Все мы играли в потрясающие изометрические игры, будь то первые Diablo, Age of Empires или Commandos. При первой встрече с изометрической игрой можно задаться вопросом: двухмерная она, трёхмерная или нечто совершенно другое. Сам мир изометрических игр обладает волшебной притягательностью для разработчиков. Давайте попробуем раскрыть тайну изометрической проекции и создадим простой изометрический уровень.

Для этого я решил использовать Phaser с кодом на JS. В результате у нас получится интерактивное приложение HTML5.

Учтите, что это не туториал по разработке на Phaser, мы просто используем его для удобного ознакомления с базовыми концепциями создания изометрической сцены. Кроме того, в Phaser есть простые способы создания изометрического контента, например, Phaser Isometric Plugin.

Для упрощения при создании сцены мы будем использовать тайлы.

1. Игры на основе тайлов

В двухмерных тайловых играх каждый визуальный элемент разбивается на мелкие части стандартного размера, называемые тайлами. Из таких тайлов на основании данных уровня (обычно это двухмерный массив) формируется игровой мир.

Чаще всего в тайловых играх используется вид сверху или сбоку. Давайте представим стандартный двухмерный вид сверху с двумя тайлами — тайлом травы и тайлом стены, показанными на рисунке:

Оба этих тайла являются квадратными изображениями одного размера, то есть высота и ширина тайла одинаковы. Предположим, что уровень игры представляет собой лужайку, окраниченную со всех сторон стенами. В таком случае данные уровня представляют собой вот такой двухмерный массив:

[
 [1,1,1,1,1,1],
 [1,0,0,0,0,1],
 [1,0,0,0,0,1],
 [1,0,0,0,0,1],
 [1,0,0,0,0,1],
 [1,1,1,1,1,1]
 ]

Здесь 0 обозначает тайл травы, а 1 — тайл стены. Расположив тайлы согласно данным уровня, мы создадим огороженную лужайку, показанную на рисунке:

Можно сделать ещё один шаг и добавить угловые тайлы, а также отдельные тайлы вертикальных и горизонтальных стен. Для этого потребуется пять дополнительных тайлов, кроме того, придётся изменить данные уровня:

[
 [3,1,1,1,1,4],
 [2,0,0,0,0,2],
 [2,0,0,0,0,2],
 [2,0,0,0,0,2],
 [2,0,0,0,0,2],
 [6,1,1,1,1,5]
 ]

См. изображение ниже, где я пометил тайлы числами, соответствующими их значениям в данных уровня:

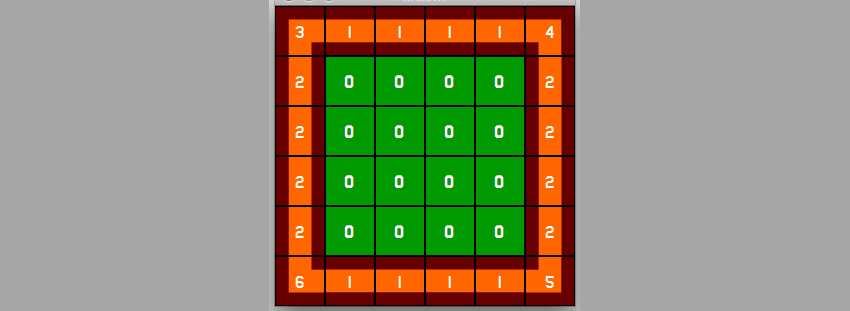
Мы разобрались с понятием тайловых уровней, давайте теперь посмотрим, как использовать простой псевдокод двухмерной сетки для сборки нашего уровня:

for (i, loop through rows)
    for (j, loop through columns)
        x = j * tile width
        y = i * tile height
        tileType = levelData[i][j]
        placetile(tileType, x, y)

Если использовать показанные выше изображения тайлов с равной шириной и высотой, то у нас получатся одинаковые размерности уровня. Если ширина и высота тайла в нашем примере равны 50 пикселям, то общий размер уровня составит 300 на 300 пикселей.

Как сказано выше, обычно тайлы используются в играх с видом сверху или сбоку. Для изометрического вида нам нужно реализовать изометрическую проекцию.

2. Изометрическая проекция

Лучшее техническое объяснение изометрической проекции, как мне кажется, дано в этой статье Клинта Белленджера:

Мы наклоняем камеру по двум осям (поворачиваем камеру на 45 градусов вбок, потом на 30 градусов вниз). При этом создаётся ромбическая сетка, в которой ширина ячеек в два раза больше высоты. Такой стиль стал популярным благодаря стратегическим играм и экшн-RPG. Если посмотреть в этом виде на куб, то мы видим три его стороны (верхнюю и две боковые).

Хотя это звучит немного сложно, реализация такого вида довольно проста. Нам нужно разобраться в том, как соотносятся двухмерное и изометрическое пространства, то есть понять связь между данными уровня и видом. Нам нужно преобразовать декартовы координаты вида сверху в изометрические координаты. На рисунке ниже показано графическое преобразование:

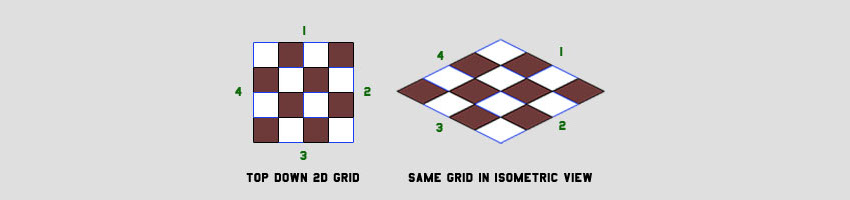
Размещение изометрических тайлов

Попробуем упростить связь между данными уровня, хранящимися в двухмерном массиве, и изометрическим видом, то есть процесс преобразования декартовых координат в изометрические. Мы создадим изометрический вид для нашей огороженной лужайки. Двухмерная реализация этого уровня представляла собой простую итерацию с двумя циклами, располагающую квадратные тайлы со смещением на их ширину и высоту. Для изометрического вида псевдокод остаётся тем же, но меняется функция placeTile().

Исходная функция просто отрисовывает изображения тайлов в переданных ей x и y, а для изометрического вида нам нужно вычислить соответствующие изометрические координаты. Уравнения для этого представлены ниже. isoX и isoY обозначают изометрические координаты X и Y, а cartX и cartY — декартовы координаты X и Y:

//Преобразование из декартовых в изометрические координаты:
 
isoX = cartX - cartY;
isoY = (cartX + cartY) / 2;

//Преобразование из изометрических в декартовы координаты:
 
cartX = (2 * isoY + isoX) / 2;
cartY = (2 * isoY - isoX) / 2;

Да, вот и всё. Эти простые уравнения творят магию изометрического проецирования. Вот вспомогательные функции Phaser, которые можно использовать для преобразования из одной системы в другую с помощью очень удобного класса Point:

function cartesianToIsometric(cartPt){
    var tempPt=new Phaser.Point();
    tempPt.x=cartPt.x-cartPt.y;
    tempPt.y=(cartPt.x+cartPt.y)/2;
    return (tempPt);
}

function isometricToCartesian(isoPt){
    var tempPt=new Phaser.Point();
    tempPt.x=(2*isoPt.y+isoPt.x)/2;
    tempPt.y=(2*isoPt.y-isoPt.x)/2;
    return (tempPt);
}

Итак, мы можем использовать вспомогательный метод cartesianToIsometric для преобразования входных 2D-координат в изометрические внутри метода placeTile. За исключением этого, код отображения остаётся тем же, но нам нужно создать новые картинки тайлов. Мы не можем использовать старые квадратные тайлы из вида сверху. На рисунке ниже показаны новые изометрические тайлы травы и стен вместе с готовым изометрическим уровнем:

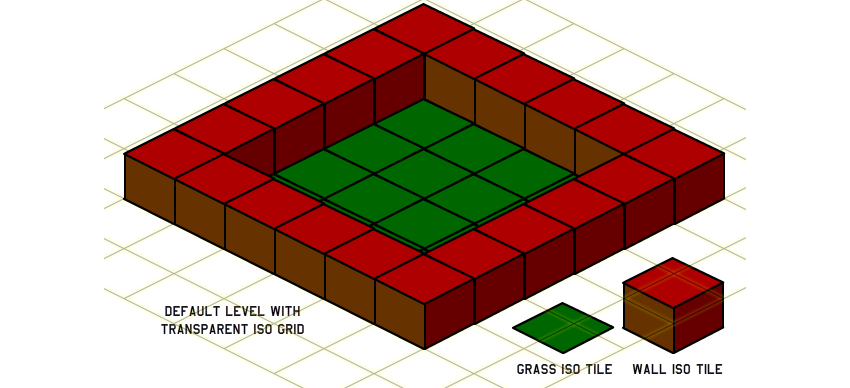
Невероятно, правда? Давайте посмотрим, как обычное двухмерное положение преобразуется в изометрическое:

2D point = [100, 100];
// изометрическая точка вычисляется следующим образом
isoX = 100 - 100; // = 0
isoY = (100 + 100) / 2;  // = 100
Iso point == [0, 100];

То есть входные данные [0, 0] преобразуются в [0, 0], а [10, 5] — в [5, 7.5].

Для нашей огороженной лужайки мы можем определить проходимые области, проверяя, равно ли значение элемента массива 0 в нужной координате. Если равно, то это трава. Для этого нам нужно определять координаты массива. Мы можем найти координаты тайла в данных уровня из его декартовых координат с помощью этой функции:

function getTileCoordinates(cartPt, tileHeight){
    var tempPt=new Phaser.Point();
    tempPt.x=Math.floor(cartPt.x/tileHeight);
    tempPt.y=Math.floor(cartPt.y/tileHeight);
    return(tempPt);
}

(Здесь мы предполагаем, что высота и ширина тайла одинаковы, как и бывает в большинстве случаев.)

То есть, зная пару экранных (изометрических) координат, мы можем найти координаты тайла вызовом функции:

getTileCoordinates(isometricToCartesian(screen point), tile height);

Эта точка на экране может быть, скажем, положением курсора мыши или подбираемого предмета.

Точки регистрации

Во Flash можно выбирать произвольные точки графики в качестве базовой точки или [0,0]. Аналогом этого в Phaser является Pivot. Когда мы располагаем графику, скажем, в точке [10,20], то эта точка Pivot соответствует [10,20]. По умолчанию [0,0] или Pivot считается левая верхняя точка. Если вы попробуете создать приведённый выше уровень с помощью этого кода, то вы не получите нужного результата. Вместо этого у вас получится плоская земля без стен, как показано ниже:

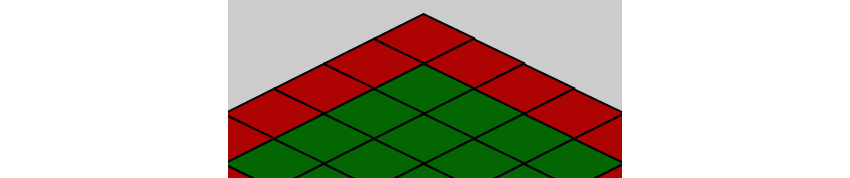
Так происходит потому, что изображения тайлов имеют разные размеры, и мы не учитываем атрибут высоты тайла стены. На рисунке ниже показаны разные используемые нами изображения тайлов и белый круг, в котором по умолчанию находится их [0,0]:

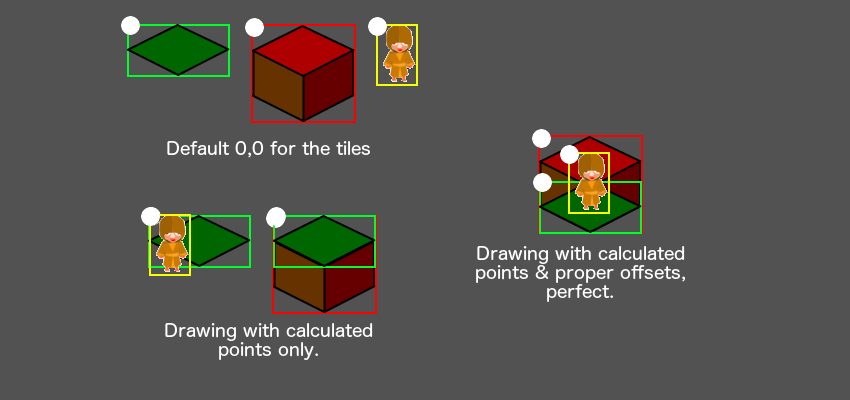
Заметьте, что при использовании базовых точек (Pivot) по умолчанию герой находится не в том месте. Также заметьте, что мы теряем высоту стены, когда отрисовываем её с базовой точкой по умолчанию. На рисунке справа показано, как они должны быть расположены правильно, чтобы у тайла стены учитывалась её высота, а герой находился посередине тайла травы. Эту проблему можно решить разными способами.

1. Сделать размеры изображений всех тайлов одинаковыми, и правильно расположить в изображении графику. При этом в каждом изображении тайла создаётся множество пустых областей.
2. Вручную устанавливать базовую точку для каждого тайла, чтобы они располагались правильно.
3. Отрисовывать тайлы с определённым смещением.

Для этого туториала я выбрал третий способ, потому что он будет работать даже во фреймворке, в котором нельзя изменять базовые точки.

3. Движение в изометрических координатах

Никогда не следует двигать персонажей или объекты в изометрических координатах напраямую. Вместо этого мы будем управлять данными игрового мира в декартовых координатах и просто использовать приведённые выше функции для обновления положения на экране. Например, если мы хотим переместить персонажа вперёд в положительном направлении по оси Y, то можно просто увеличить его свойство y в двухмерных координатах, а затем преобразовать конечное положение в изометрические координаты:

y = y + speed;
placetile(cartesianToIsometric(new Phaser.Point(x, y)))

Давайте подведём итог всем новым понятиям, которые мы изучили, и попробуем реализовать рабочий пример объекта, двигающегося в изометрическом мире. Можно использовать необходимые графические ресурсы из папки assets в репозитории исходного кода на git.

Сортировка по глубине

Если вы пробовали перемещать изображение мяча в огороженном саду, то заметили проблемы с сортировкой по глубине. Если в изометрическом мире есть подвижные элементы, то кроме обычного расположения, нам нужно позаботиться и о сортировке по глубине. Правильная сортировка гарантирует, что объекты, находящиеся ближе к экрану, будут отрисовываться поверх более далёких объектов. Как упомянуто в этой статье, простейший способ сортировки — использование декартовой координаты Y: чем выше объект на экране, тем раньше его следует отрисовывать. Это может неплохо работать для простых изометрических сцен, но лучше будет перерисовывать всю изометрическую сцену в процессе движения в соответствии с координатами тайла в массиве. Давайте я подробно объясню этот подход на примере псевдокода отрисовки уровня:

for (i, loop through rows)
    for (j, loop through columns)
        x = j * tile width
        y = i * tile height
        tileType = levelData[i][j]
        placetile(tileType, x, y)

Представьте, что объект или персонаж находится на тайле [1,1], то есть на самом верхнем зелёном тайле в изометрическом виде. Для правильной отрисовки уровня персонаж нужно отрисовывать после отрисовки углового тайла стены, левого и правого тайла стены, а также земли, как показано на рисунке:

Если мы будем выполнять цикл отрисовки в соответствии с псевдокодом, то сначала будет отрисована средняя угловая стена, затем цикл продолжит отрисовывать все стены в верхней правой части, пока не достигнет правого угла. В следующем цикле он отрисует стену слева от персонажа, а затем тайл травы, на котором стоит персонаж. Поскольку мы определили, что это тайл, который занимает персонаж, то отрисовываем персонажа после тайла травы. Таким образом, если бы на свободных трёх тайлах травы рядом с тайлом персонажа находились стены, то эти стены перекрывали персонажа, обеспечивая правильную сортировку по глубине.

4. Создание графики

Изометрическая графика может, но не обязана быть пиксель-артом. При работе с изометрическим пиксель-артом полезно изучить руководство RhysD, в котором содержится всё необходимое. Теорию можно изучить в Википедии.

При создании изометрической графики нужно соблюдать следующие правила:

• Начните с пустой изометрической сетки и придерживайтесь её с попиксельной точностью.
• Старайтесь разбивать графику на простые изометрические тайловые изображения.
• Сделайте так, чтобы каждый тайл был или проходимым, или непроходимым. Иначе сложно будет работать с тайлами, содержащими и проходимые, и непроходимые области.
• Большинство тайлов должно быть бесшовным, чтобы ими можно было замостить уровень в любом направлении.
• Тени создавать сложно, если вы не используете решение со слоями, при котором сначала отрисовываются тени на слое земли, а потом на верхнем слое отрисовывается персонаж (или деревья и другие объекты). Если вы не используете несколько слоёв, то сделайте так, чтобы тени падали вперёд и, например, не закрывали героя, стоящего за деревом.
• Если вам нужно использовать изображение тайла больше, чем стандартный размер изометрического тайла, то постарайтесь подобрать размер, кратный стандартному размеру тайла. В таких случаях лучше использовать слои, чтобы можно было разрезать графику на разные куски в зависимости от её высоты. Например, дерево можно разрезать на три части — корень, ствол и листву. Так будет проще сортировать глубины, потому что можно будет отрисовывать части в соответствующих слоях, соотносящихся с их высотами.

Изометрические тайлы больше единичного размера тайла создают проблемы при сортировке по глубине. Такие проблемы рассмотрены в следующих статьях:

Посты по теме

• Bigger tiles
• Splitting and Painter's algorithm
• OpenSpace's post on effective ways of splitting up larger tiles

5. Изометрические персонажи

Для начала нам нужно определиться с тем, в каких направлениях можно перемещаться в нашей игре. Обычно в играх разрешается движение в четырёх или восьми направлениях. Посмотрите на рисунок ниже, чтобы понять связь между двухмерным и изометрическим пространством:

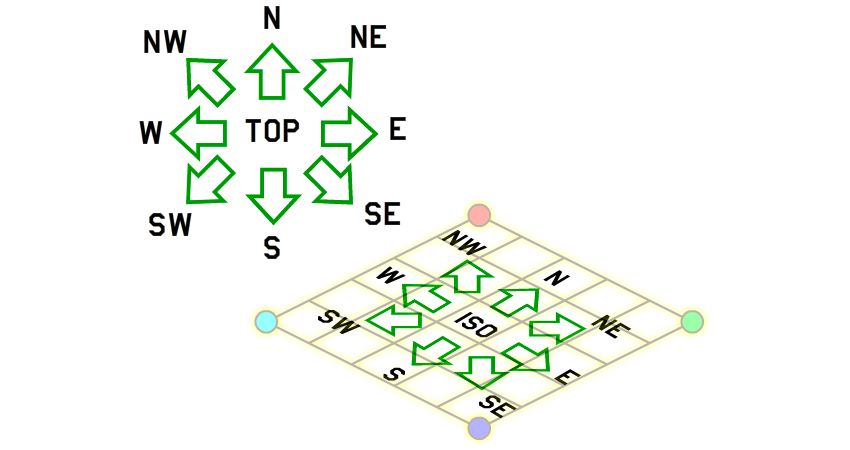
Обратите внимание, что в игре с видом сверху при нажатии на клавишу вверх персонаж будет двигаться вертикально вверх, но в изометрической игре он переместится под углом в 45 градусов в сторону верхнего правого угла.

Для вида сверху мы можем создать один набор анимаций персонажа, смотрящего в одном направлении, а потом просто повернуть все анимации. Для графики изометрического персонажа нужно создать анимацию для каждого из допустимых направлений, то есть для движения в восьми направлениях нужно создать по восемь анимаций для каждого действия.

Для простоты понимания направления обычно обозначают как «север», «северо-запад», «запад» и так далее. В кадрах персонажа на рисунке показаны кадры неподвижного положения, начиная с юго-востока и по часовой стрелке:

Мы будем располагать персонажей так же, как располагали тайлы. Движение персонажа выполняется вычислением декартовых координат и преобразованием их в изометрические. Допустим, для управления персонажем используется клавиатура.

Мы назначим две переменные, dX и dY, значение которых зависит от нажатых клавиш управления. По умолчанию эти переменные равны 0, а значения им присваиваются согласно таблице внизу, где В, Н, П и Л означают, соответственно верхнюю, нижнюю, правую и левую клавиши направления. Значение 1 под клавишей означает, что клавиша нажата, 0 — что она не нажата.

Клавиша    Положение
В Н П Л    dX dY
================
0 0 0 0     0  0
1 0 0 0     0  1
0 1 0 0     0 -1
0 0 1 0     1  0
0 0 0 1    -1  0
1 0 1 0     1  1
1 0 0 1    -1  1
0 1 1 0     1 -1
0 1 0 1    -1 -1

Теперь с помощью значений dX и dY мы можем обновлять декартовы координаты следующим образом:

newX = currentX + (dX * speed);
newY = currentY + (dY * speed);

Итак, dX и dY представляют собой изменение положения персонажа по X и Y в зависимости от нажатых клавиш. Как сказано выше, мы легко можем вычислить новые изометрические координаты:

Iso = cartesianToIsometric(new Phaser.Point(newX, newY))

Получив новое изометрическое положение, мы должны переместить персонажа в это положение. На основании значений dX и dY мы можем понять, в каком направлении смотрит персонаж и использовать соответствующую анимацию. После перемещения персонажа не забывайте перерисовать уровень с соответствующей сортировкой по глубине, потому что тайловые координаты персонажа могут измениться.

Распознавание коллизий

Распознавание коллизий выполняется проверкой того, является ли тайл в новом вычисленном положении объекта непроходимым. Итак, после нахождения нового положения мы не можем сразу же перемещать туда персонажа, нам нужно сначала проверить, что за тайл занимает это место.

tile coordinate = getTileCoordinates(isometricToCartesian(current position), tile height);
if (isWalkable(tile coordinate)) {
  moveCharacter();
} else {
  //ничего не делать;
}

В функции isWalkable() мы проверяем, является ли значение массива данных уровня в заданной координате проходимым тайлом. Нам нужно также обновлять направление, в котором смотрит персонаж, даже если он не движется, на случай, если он столкнулся с непроходимым тайлом.

Это похоже на правильное решение, но оно будет работать только для объектов без объёма. Для вычисления коллизий мы рассматриваем только одну точку (центральную точку персонажа). В действительности нам нужно найти все четыре угла из заданной двухмерной центральной точки и вычислить коллизии для всех этих углов. Если какой-то из углов попадает в непроходимый тайл, то перемещать персонажа нельзя.

Сортировка по глубине с персонажами

Рассмотрим персонажа и тайл дерева в изометрическом мире, имеющие одинаковые размеры изображения, как бы неестественно это ни выглядело.

Чтобы хорошо разобраться в сортировке по глубине, нам нужно понять, что когда координаты X и Y персонажа меньше, чем у дерева, то дерево перекрывает персонажа. Когда координаты X и Y персонажа больше, чем у дерева, то персонаж перекрывает дерево. Когда их координаты X равны, то решение принимается только по координате Y: объект с большей координатой Y перекрывает другой. Если совпадают координаты Y, то решение принимается только по X: объект с большим X перекрывает другой.

Как сказано выше, упрощённая версия алгоритма заключается в простой отрисовке уровней от дальних тайлов (т.е. tile[0][0]) к ближним, строка за строкой. Если персонаж занимает тайл, то сначала мы рисуем тайл земли, а потом отрисовываем тайл персонажа. Это сработает хорошо, потому что персонаж не может занимать тайл стены.

6. Время для демо!

Вот демо на Phaser. Нажмите мышью для переключения на интерактивную область, а потом управляйте персонажем клавишами со стрелками. Для перемещения по диагонали нажимайте две клавиши.

7. Собираемые предметы

Собираемые предметы — это объекты, которые можно подбирать на уровне, обычно просто наступая на них. Например это могут быть монеты, кристаллы, боеприпасы и т.д.

Данные о предметах можно хранить прямо в данных уровня, как показано ниже:

[
[1,1,1,1,1,1],
[1,0,0,0,0,1],
[1,0,8,0,0,1],
[1,0,0,8,0,1],
[1,0,0,0,0,1],
[1,1,1,1,1,1]
]

В этих данных уровня мы используем 8 для обозначения предмета на тайле травы (1 и 0, как и раньше, обозначают траву и стены). Это может быть тайловое изображение с тайлом травы, на которое наложено изображение предмета. По этой логике нам понадобятся два различных состояния тайла для каждого тайла, на котором может находиться предмет: один с предметом, и другой без него, который отображается после получения предмета.

Обычно в изометрической графике бывает множество проходимых тайлов. Допустим, у нас их 30. Если использовать приведённый выше подход, то если у нас есть N поднимаемых предметов, к уже имеющимся 30 тайлам потребуется ещё N x 30. Это не очень эффективно. Поэтому нам стоит создавать такие сочетания динамически. Для решения этой задачи можно использовать тот же способ, который мы использовали выше для размещения персонажа. Когда мы доходим до тайла с предметом, мы сначала отрисовываем тайл травы, а потом помещаем на него предмет. Таким образом в дополнение к 30 проходимым тайлам нам потребуется всего N тайлов предметов, но нам нужны будут числовые значения для обозначения каждого сочетания в данных уровня. Чтобы не вводить N x 30 значений, можно хранить отдельный массив pickupArray для хранения данных о предметах, отдельно от levelData. Законченный уровень с предметом показан ниже:

В нашем примере я сделаю проще и не буду использовать отдельный массив для предметов.

Собирание предметов

Распознавание предметов выполняется точно так же, как и распознавание коллизий, но после перемещения персонажа.

if(onPickupTile()){
    pickupItem();
}


function onPickupTile(){//проверяем, есть ли предмет на тайле с персонажем
    return (levelData[heroMapTile.y][heroMapTile.x]==8);
}

В функции onPickupTile(), мы проверяем, является ли значение массива levelData в координате heroMapTile тайлом с предметом. Число в массиве levelData в координате этого тайла обозначает тип предмета. Мы проверяем коллизии до перемещения персонажа, но проверка предметов выполняется после: в случае коллизий персонаж не сможет занять точку, если она уже занята непроходимым тайлом, а в случае предметов персонаж может свободно может сдвинуться на тайл.

Стоит также заметить, что данные коллизий обычно никогда не меняются, а данные о предметах изменяются, когда мы подбираем предмет. (При этом обычно просто меняется значение в массиве levelData, например, с 8 на 0.)

Это приводит к проблеме: что случится, когда нам нужно перезапустить уровень, то есть восстановить все предметы на их исходных точках? У нас нет информации для этого, потому что массив levelData изменяется при поднятии предмета. Решение заключается в использовании копии массива уровня в процессе игры и сохранении неизменного массива levelData. Например, мы используем levelData и levelDataLive[], клонируем последний из первого при начале уровня, а затем меняем в процессе игры только levelDataLive[].

Например, я создаю случайный предмет на свободном тайле травы после каждого собранного предмета и увеличиваю значение pickupCount. Функция pickupItem выглядит следующим образом:

function pickupItem(){
    pickupCount++;
    levelData[heroMapTile.y][heroMapTile.x]=0;
    //создаём следующий собираемый предмет
    spawnNewPickup();
}

Вы наверно заметили, что мы проверяем наличие предметов всегда, когда персонаж находится на тайле. Это может может происходить несколько раз в секунду (мы проверяем только когда пользователь двигается, но в одном тайле мы можем повторять раз за разом), но приведённая выше логика будет выполняться безошибочно. Как только мы присвоим данным массива levelData значение 0 при первом обнаружении поднятия предмета, все последующие проверки onPickupTile() будут возвращать для тайла false. Посмотрите этот интерактивный пример.

8. Тайлы-триггеры

Как понятно из названия, тайлы-триггеры запускают какие-то действия, когда игрок наступает на них или нажимает на них клавишу. Они могут телепортировать игрока в другое место, открывать ворота, создавать врагов и так далее. В каком-то смысле, собираемые предметы являются просто особым типом триггеров: когда игрок наступает на тайл с монетой, монета исчезает, а счётчик монет увеличивается.

Давайте посмотрим, как можно реализовать дверь, переносящую игрока на другой уровень. Тайл рядом с дверью будет триггером. Когда игрок нажимает клавишу x, то перемещается на другой уровень.

Для смены уровней нужно всего лишь заменить текущий массив levelData на массив нового уровня, а затем назначить новое положение и направление heroMapTile персонажа. Допустим, есть два уровня с дверями, через которые можно проходить. Поскольку тайл земли рядом с дверью будет активным тайлом в обоих уровнях, можно использовать его в качестве нового положения персонажа, появляющегося на уровне.

Логика реализации здесь такая же, как и для собираемых предметов. Для хранения значений тайлов-триггеров мы снова используем массив levelData. В нашем примере 2 будет означать тайл с дверью, а значение рядом с ним будет триггером. Я использовал 101 и 102, решив, что любой тайл со значением больше 100 будет активным тайлом, а значение минус 100 будет уровнем, на который он ведёт:

var level1Data=
[[1,1,1,1,1,1],
[1,1,0,0,0,1],
[1,0,0,0,0,1],
[2,102,0,0,0,1],
[1,0,0,0,1,1],
[1,1,1,1,1,1]];

var level2Data=
[[1,1,1,1,1,1],
[1,0,0,0,0,1],
[1,0,8,0,0,1],
[1,0,0,0,101,2],
[1,0,1,0,0,1],
[1,1,1,1,1,1]];

Код проверки на событие срабатывания триггера показан ниже:

var xKey=game.input.keyboard.addKey(Phaser.Keyboard.X);

xKey.onUp.add(triggerListener);// добавление Signal listener для события up

function triggerListener(){
    var trigger=levelData[heroMapTile.y][heroMapTile.x];
    if(trigger>100){//активный тайл
        trigger-=100;
        if(trigger==1){//переход на уровень 1
            levelData=level1Data;
        }else {//переход на уровень 2
            levelData=level2Data;
        }
        for (var i = 0; i < levelData.length; i++)
        {
            for (var j = 0; j < levelData[0].length; j++)
            {
                trigger=levelData[i][j];
                if(trigger>100){//находим новый активный тайл и помещаем на него персонажа
                    heroMapTile.y=j;
                    heroMapTile.x=i;
                    heroMapPos=new Phaser.Point(heroMapTile.y * tileWidth, heroMapTile.x * tileWidth);
                    heroMapPos.x+=(tileWidth/2);
                    heroMapPos.y+=(tileWidth/2);
                }
            }
        }
    }
}

Функция triggerListener() проверяет, больше ли 100 значение массива данных триггеров в заданной координате. Если это так, то мы определяем, на какой уровень нам нужно перейти, вычтя 100 из значения тайла. Функция находит тайл-триггер в новом levelData, который будет координатой создания персонажа. Я сделал так, чтобы триггер активировался при отпускании клавиши x; если просто считывать нажатую клавишу, то мы окажемся в цикле, который будет перебрасывать нас между уровнями, пока нажата клавиша, потому что персонаж всегда создаётся на новом уровне на активном тайле.

Вот работающее демо. Попробуйте пособирать предметы, наступая на них, и менять уровни, встав перед дверью и нажав x.

9. Снаряды

Снарядами мы будем называть то, что движется в определённом направлении с определённой скоростью, например, пуля, волшебное заклинание, мяч и т.д. К снарядам применимо всё, относящееся к персонажам, за исключением высоты: снаряды обычно не катятся по земле, а летят на определённой высоте. Пуля летит на уровне талии персонажа, а мяч может даже скакать.

Интересно, что изометрическая высота соответствует высоте в двухмерном виде сбоку, хотя и меньше по величине. Здесь нет сложных преобразований. Если мяч в декартовых координатах находится в десяти пикселях над землёй, то в изометрических координатах он может быть над землёй в 10 или 6 пикселях. (В нашем случае соответствующей осью будет ось Y.)

Давайте попробуем реализовать мяч, скачущий по нашему огороженному саду. Для дополнительного реализма мы добавим мячу тень. Всё, что нужно — прибавлять к изометрическому значению Y мяча значение высоты отскока. Значение высоты отскока будет меняться покадрово в зависимости от гравитации, и как только мяч коснётся земли, мы сменим знак текущей скорости по оси Y.

Прежде чем мы начнём разбираться с скачками в изометрической системе, попробуем реализовать их в двухмерной декартовой системе. Обозначим силу отскока мяча переменной zValue. Для начала представим, что сила отскока мяча равна 100, то есть zValue = 100.

Мы используем две переменные: incrementValue, которая изначально имеет значение 0, и gravity, имеющая значение -1. В каждом кадре мы будем вычитать incrementValue из zValue и вычитать gravity из incrementValue для создания эффекта затухания. Когда zValue достигает 0, это значит, что мяч достиг земли. В этот момент мы меняем знак incrementValue, умножив её на -1, и превратив в положительное число. Это значит, что со следующего кадра мяч начнёт двигаться вверх, то есть отскочит.

Вот как это выглядит в коде:

if(game.input.keyboard.isDown(Phaser.Keyboard.X)){
    zValue=100;
}
incrementValue-=gravity;
zValue-=incrementValue;
if(zValue<=0){
    zValue=0;
    incrementValue*=-1;
}

Для изометрического вида код тоже остался тем же, с небольшой разницей: мы используем меньшее начальное значение zValue. Ниже показано, как zValue прибавляет к значению изометрической координаты y мяча при отрисовке.

function drawBallIso(){
    var isoPt= new Phaser.Point();//Не рекомендуется создавать точки в цикле обновления
    var ballCornerPt=new Phaser.Point(ballMapPos.x-ball2DVolume.x/2,ballMapPos.y-ball2DVolume.y/2);
    isoPt=cartesianToIsometric(ballCornerPt);//находим новое изометрическое положение для персонажа из положения на двухмерной карте
    gameScene.renderXY(ballShadowSprite,isoPt.x+borderOffset.x+shadowOffset.x, isoPt.y+borderOffset.y+shadowOffset.y, false);//отрисовка тени на текстуре рендера
    gameScene.renderXY(ballSprite,isoPt.x+borderOffset.x+ballOffset.x, isoPt.y+borderOffset.y-ballOffset.y-zValue, false);//отрисовка персонажа на текстуре рендера
}

См. интерактивный пример.

Играемая тенью роль очень важна, она добавляет реализма этой иллюзии. Кроме того, заметьте, что теперь мы используем две экранные координаты (x и y) для представления трёх измерений в изометрических координатах — ось Y в экранных координатах также является осью Z в изометрических координатах. Это может запутать.

10. Нахождение пути и движение по нему

Поиск пути и движение по нему — это довольно сложный процесс. Для нахождения пути между двумя точками существует множество разных решений с использованием различных алгоритмов, но поскольку levelData является двухмерным массивом, то всё гораздо проще, чем могло бы быть. У нас есть чётко заданные уникальные узлы, которые может занимать игрок, и мы можем легко проверить, можно ли по ним пройти.

Посты по теме

• A* Pathfinding for Beginners
• Goal-Based Vector Field Pathfinding
• Speed Up A* Pathfinding With the Jump Point Search Algorithm
• The «Path Following» Steering Behavior

Подробный обзор алгоритмов поиска путей слишком велик для этой статьи, но я постараюсь объяснить наиболее распространённый способ: алгоритм кратчайшего пути, самыми известными реализациями которого являются A* и алгоритм Дейкстры.

Наша цель — найти узлы, соединяющие начальный узел с конечным. Из начального узла мы посещаем все восемь соседних узлов, и помечаем их как посещённые. Этот процесс рекурсивно повторяется для каждого нового посещённого узла.

Каждый поток отслеживает посещённые узлы. При переходе к соседним узлам уже посещённые узлы пропускаются (рекурсия прекращается). Процесс продолжается, пока мы не достигнем конечного узла, в котором рекурсия завершается и весь пройденный путь возвращается как массив узлов. Иногда конечный узел достигнуть не удаётся, то есть поиск пути заканчивается неудачей. Обычно мы находим между узлами несколько путей. В таком случае мы выбираем один из них с минимальным количеством узлов.

Поиск пути

Глупо изобретать велосипед заново, если речь идёт о чётко описанных алгоритмах, поэтому для поиска пути мы будем использовать уже существующие решения. В Phaser нам потребуется решение на JavaScript, поэтому я выбрал EasyStarJS. Инициализация движка поиска пути выполняется следующим образом:

easystar = new EasyStar.js();
easystar.setGrid(levelData);
easystar.setAcceptableTiles([0]);
easystar.enableDiagonals();// мы хотим, чтобы в пути были диагонали
easystar.disableCornerCutting();// без диагональных путей при движении в углах стен

Поскольку в массиве levelData содержатся только 0 и 1, мы можем сразу передать его в массив узлов. Значением 0 мы обозначили проходимый узел. Также мы включили возможность движения по диагонали, но отключили её, когда движение происходит рядом с углами непроходимых тайлов.

Так сделано потому, что при диагональном движении персонаж может врезаться в непроходимый тайл. В таком случае система распознавания коллизий не позволит персонажу пройти насквозь. Кроме того, следует учесть, что в примере я полностью удалил распознавание столкновений, потому что в нашем примере персонажа по пути будет двигать искусственный интеллект и оно не требуется.

Мы будем распознавать нажатие мышью на любой свободный тайл в уровне и вычислять путь с помощью функции findPath. Callback-метод plotAndMove получает массив узлов созданного пути. Мы помечаем найденный путь на миникарте.

game.input.activePointer.leftButton.onUp.add(findPath)

function findPath(){
    if(isFindingPath || isWalking)return;
    var pos=game.input.activePointer.position;
    var isoPt= new Phaser.Point(pos.x-borderOffset.x,pos.y-borderOffset.y);
    tapPos=isometricToCartesian(isoPt);
    tapPos.x-=tileWidth/2;//настройка для нахождения нужного тайла для ошибки из-за округления
    tapPos.y+=tileWidth/2;
    tapPos=getTileCoordinates(tapPos,tileWidth);
    if(tapPos.x>-1&&tapPos.y>-1&&tapPos.x<7&&tapPos.y<7){//нажатие мышью внутри сетки
        if(levelData[tapPos.y][tapPos.x]!=1){//не тайл стены
            isFindingPath=true;
            //алгоритм делает своё дело
            easystar.findPath(heroMapTile.x, heroMapTile.y, tapPos.x, tapPos.y, plotAndMove);
            easystar.calculate();
        }
    }
}
function plotAndMove(newPath){
    destination=heroMapTile;
    path=newPath;
    isFindingPath=false;
    repaintMinimap();
    if (path === null) {
        console.log("No Path was found.");
    }else{
        path.push(tapPos);
        path.reverse();
        path.pop();
        for (var i = 0; i < path.length; i++)
        {
            var tmpSpr=minimap.getByName("tile"+path[i].y+"_"+path[i].x);
            tmpSpr.tint=0x0000ff;
            //console.log("p "+path[i].x+":"+path[i].y);
        }
        
    }
}

Движение по пути

Получив путь в виде массива узлов, мы должны заставить персонажа двигаться по нему.

Допустим, мы хотим, чтобы персонаж двигался к тайлу, по которому мы щёлкнули. Сначала мы ищем путь между узлом, занимаемым персонажем, и узлом, по которому щёлкнули. Если путь найден, то нам нужно переместить персонажа в первый узел массива узлов, пометив его как точку назначения. Добравшись до узла назначения, мы проверяем, есть ли ещё узлы в массиве узлов, и если есть, то помечаем как точку назначения следующий узел, и так далее, пока не достигнем конечного узла.

Также каждый раз при достижении узла мы будем менять направление игрока на основании текущего узла и нового узла назначения. Между узлами мы просто ходим в нужном направлении, пока не достигнем узла назначения. Это очень простой ИИ, и в нашем примере он реализован в методе aiWalk, частично показанном ниже:

function aiWalk(){
    if(path.length==0){//путь закончился
        if(heroMapTile.x==destination.x&&heroMapTile.y==destination.y){
            dX=0;
            dY=0;
            isWalking=false;
            return;
        }
    }
    isWalking=true;
    if(heroMapTile.x==destination.x&&heroMapTile.y==destination.y){//достигли текущей точки назначения, задаём новую, меняем направление
        //перед поворотом ждём, пока не войдём на несколько шагов на тайл
        stepsTaken++;
        if(stepsTaken<stepsTillTurn){
            return;
        }
        console.log("at "+heroMapTile.x+" ; "+heroMapTile.y);
        //ставим персонажа в центр тайла    
        heroMapSprite.x=(heroMapTile.x * tileWidth)+(tileWidth/2)-(heroMapSprite.width/2);
        heroMapSprite.y=(heroMapTile.y * tileWidth)+(tileWidth/2)-(heroMapSprite.height/2);
        heroMapPos.x=heroMapSprite.x+heroMapSprite.width/2;
        heroMapPos.y=heroMapSprite.y+heroMapSprite.height/2;
        
        stepsTaken=0;
        destination=path.pop();//узнаём следующий тайл в пути
        if(heroMapTile.x<destination.x){
            dX = 1;
        }else if(heroMapTile.x>destination.x){
            dX = -1;
        }else {
            dX=0;
        }
        if(heroMapTile.y<destination.y){
            dY = 1;
        }else if(heroMapTile.y>destination.y){
            dY = -1;
        }else {
            dY=0;
        }
        if(heroMapTile.x==destination.x){
            dX=0;
        }else if(heroMapTile.y==destination.y){
            dY=0;
        }
        //......
    }
}

Нам нужно отфильтровывать правильные точки нажатия мышью. Для этого мы определяем, что мы нажали в проходимой области, а не на тайле стены или другом непроходимом тайле.

Ещё один интересный момент кодирования ИИ: мы не хотим, чтобы персонаж поворачивался лицом к следующему тайлу в массиве узлов как только он дойдёт до текущего, потому что такой мгновенный поворот приведёт к том, что персонаж будет ходить по границам тайлов. Вместо этого нам следует подождать, пока персонаж на несколько шагов зайдёт на тайл, а потом уже начинать искать следующую точку назначения. Также лучше вручную помещать персонажа в середину текущего тайла прямо перед поворотом, чтобы всё выглядело наилучшим образом.

Можно посмотреть работающее демо.

11. Изометрический скроллинг

Когда область уровня гораздо больше экранной области, то необходимо выполнять скроллинг.

Видимую экранную область можно рассматривать как небольшой прямоугольник в большом прямогольнике всей области уровня. Скроллинг является простым перемещением внутреннего прямоугольника во внутреннем. Обычно в процессе скроллинга положение персонажа в экранном прямоугольнике остаётся постоянным — чаще всего он находится в центре экрана. Интересно, что для реализации скроллинга нам нужно всего лишь отслеживать угловую точку внутреннего прямоугольника.

Эта угловая точка, которую мы обозначаем в декартовых координатах, попадает в один из тайлов в данных уровня. Для скроллинга мы увеличиваем положение угловой точки по осям X и Y в декартовых координатах. Теперь мы можем преобразовать эту точку в изометрические координаты и использовать их для отрисовки экрана.

Новые преобразованные значения в изометрическом пространстве должны быть углом экрана, то есть новыми (0, 0). Поэтому при парсинге и отрисовке данных уровня мы вычитаем это значение из изометрического положения каждого тайла. Мы можем определить, находится ли новое положение тайла в пределах экрана.

Или же мы можем отрисовывать на экране сетку изометрических тайлов размером X x Y, чтобы цикл отрисовки был эффективным для больших уровней.

Все эти шаги можно выразить следующим образом:

• Обновление декартовых координат X и Y угловой точки.
• Преобразование в изометрическое пространство.
• Вычитание этого значения из изометрического положения отрисовки каждого тайла.
• Отрисовка на экране только заданного количества тайлов, начиная с этого нового угла.
• Дополнительно: отрисовка тайла, только если новое изометрическое положение отрисовки находится в пределах экрана.

var cornerMapPos=new Phaser.Point(0,0);
var cornerMapTile=new Phaser.Point(0,0);
var visibleTiles=new Phaser.Point(6,6);

//...
function update(){
    //...
    if (isWalkable())
    {
        heroMapPos.x +=  heroSpeed * dX;
        heroMapPos.y +=  heroSpeed * dY;
        
        //перемещаем угол в противоположном направлении
        cornerMapPos.x -=  heroSpeed * dX;
        cornerMapPos.y -=  heroSpeed * dY;
        cornerMapTile=getTileCoordinates(cornerMapPos,tileWidth);
        //получаем новый тайл персонажа
        heroMapTile=getTileCoordinates(heroMapPos,tileWidth);
        //сортировка по глубине и отрисовка новой сцены
        renderScene();
    }
}
function renderScene(){
    gameScene.clear();//удаляем предыдущий кадр, потом отрисовываем заново
    var tileType=0;
    //ограничиваем цикл видимой областью
    var startTileX=Math.max(0,0-cornerMapTile.x);
    var startTileY=Math.max(0,0-cornerMapTile.y);
    var endTileX=Math.min(levelData[0].length,startTileX+visibleTiles.x);
    var endTileY=Math.min(levelData.length,startTileY+visibleTiles.y);
    startTileX=Math.max(0,endTileX-visibleTiles.x);
    startTileY=Math.max(0,endTileY-visibleTiles.y);
    //проверяем граничное условие
    for (var i = startTileY; i < endTileY; i++)
    {
        for (var j = startTileX; j < endTileX; j++)
        {
            tileType=levelData[i][j];
            drawTileIso(tileType,i,j);
            if(i==heroMapTile.y&&j==heroMapTile.x){
                drawHeroIso();
            }
        }
    }
}
function drawHeroIso(){
    var isoPt= new Phaser.Point();//Не рекомендуется создавать точки в цикле обновления
    var heroCornerPt=new Phaser.Point(heroMapPos.x-hero2DVolume.x/2+cornerMapPos.x,heroMapPos.y-hero2DVolume.y/2+cornerMapPos.y);
    isoPt=cartesianToIsometric(heroCornerPt);//находим новое изометрическое положение персонажа из положения на 2D-карте
    gameScene.renderXY(sorcererShadow,isoPt.x+borderOffset.x+shadowOffset.x, isoPt.y+borderOffset.y+shadowOffset.y, false);//отрисовываем тень на текстуре рендера
    gameScene.renderXY(sorcerer,isoPt.x+borderOffset.x+heroWidth, isoPt.y+borderOffset.y-heroHeight, false);//отрисовываем персонажа на текстуре рендера
}
function drawTileIso(tileType,i,j){//располагаем изометрические тайлы уровня
    var isoPt= new Phaser.Point();//не рекомендуется создавать точку в цикле обновления
    var cartPt=new Phaser.Point();//Добавлено для лучшей читаемости кода.
    cartPt.x=j*tileWidth+cornerMapPos.x;
    cartPt.y=i*tileWidth+cornerMapPos.y;
    isoPt=cartesianToIsometric(cartPt);
    //Можно оптимизировать дальше и не отрисовывать ничего за пределами экрана.
    if(tileType==1){
        gameScene.renderXY(wallSprite, isoPt.x+borderOffset.x, isoPt.y+borderOffset.y-wallHeight, false);
    }else{
        gameScene.renderXY(floorSprite, isoPt.x+borderOffset.x, isoPt.y+borderOffset.y, false);
    }
}

Заметьте, что приращение угловой точки происходит в направлении, противоположном направлению обновления положения персонажа при его движении. Благодаря этому персонаж остаётся на одном и том же месте относительно экрана. Посмотрите этот пример (используйте клавиши со стрелками для скроллинга, щелчок мышью для увеличения видимой сетки).

Пара примечаний:

• При скроллинге нам может понадобиться отрисовка дополнительных тайлов на границах экрана, иначе по краям экрана тайлы будут появляться и исчезать.
• Если в игре есть тайлы, занимающие несколько единичных размеров тайлов, то потребуется рисовать больше тайлов на границах. Например, если самый большой тайл из всего набора имеет размер X на Y, то потребуется отрисовывать на X больше тайлов слева и справа, и на Y больше тайлов сверху и снизу. Так мы гарантируем, что углы большого тайла будут видимы при скроллинге.
• Нам по-прежнему нужно обеспечивать отсутствие пустых областей на экране, когда отрисовка выполняется рядом с границами уровня.
• Уровень должен скроллиться только до тех пор, пока на соответствующем крае экрана не будет отрисован соответствующий крайний тайл. После этого персонаж должен продолжать двигаться в пространстве экрана без скроллинга уровня. Для этого нам нужно отслеживать все четыре угла внутреннего экранного прямоугольника и соответствующим образом управлять логикой скроллинга и перемещения персонажа. Готовы ли вы реализовать это самостоятельно?

Заключение

Этот туториал в основном предназначен для новичков, изучающих изометрические игровые миры. Многие из представленных здесь концепций имеют другие, немного более сложные решения, и я намеренно выбрал самые простые.

Возможно, это руководство не решит всех появляющихся у вас проблем, но полученная информация позволит развить эти концепции для создания более сложных решений. Например, реализованная простая сортировка по глубине не поможет в случае уровней с несколькими этажами и тайлами платформ, двигающимися с одного этажа на другой. Но это уже задача для другого туториала.

Автор: PatientZero

Источник