Ray tracing не только в 3D

Многие в общих чертах представляют, как работает лучевая трассировка: через каждый пиксель сцены алгоритм пропускает луч и вычисляет, с какими объектами сцены он пересекается и как в результате данный пиксель должен быть освещён. Алгоритм по сути требует, чтобы у нас была функция, которая для каждой позиции возвращает цвет точки. Разумеется, тот же подход можно применять не только для трёхмерной графики: любое изображение можно растеризовать таким образом, если у нас есть подходящая функция. Рассмотрим для примера, как с помощью такого подхода решить задачу визуализации диаграмм разложения на простые множители, о которой написал helarqjsc.

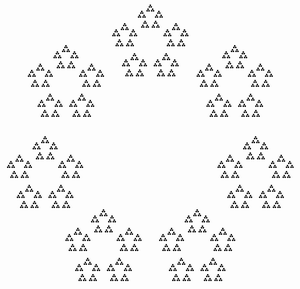
Моя реализация здесь. На картинке изображено 10! = 3628800, хотя всех деталей, разумеется, не видно.

В данной задаче, как и во многих других, цвет бинаризованный: или чёрный, или белый. Соответственно, нам нужна функция вида function check(x,y), которая возвращает логическое значение, говорящее нам, следует ли закрасить данную точку. Математики бы сказали, что check(x,y) — характеристическая функция множества точек на плоскости (в математике такая функция обычно возвращает 1 или 0). Если эта функция задана, алгоритм рисования на HTML5 Canvas будет достаточно прост:

function trace(canvas) {
  var ctx = canvas.getContext("2d");
  var w = canvas.width;
  var h = canvas.height;
  var img = ctx.createImageData(w, h);
  for(var x=0; x<w; x++)
    for(var y=0; y<h; y++)
      if(check(x,y)) img.data[(y*w+x)*4+3]=255;
  ctx.putImageData(img, 0, 0);
}

Здесь мы пользуемся тем, что createImageData создаёт чёрный прозрачный холст. Мы меняем только байт, отвечающий за прозрачность.

Пусть мы хотим изобразить, к примеру, круг с центром (50, 50) и радиусом 50. Функция check(x,y) будет выглядеть так:

function check(x,y) {
  return (x-50)*(x-50)+(y-50)*(y-50)<50*50;
}

Сумма квадратов расстояний от центра меньше квадрата радиуса. Получим такую картинку:

Разумеется, для круга проще и дешевле воспользоваться библиотечной функцией. Кроме того, наш круг получился угловатым. Чтобы с этим немного побороться, воспользуемся субпиксельным рендерингом: разделим пиксель на n×n более маленьких, прогоним check для каждого из них и установим прозрачность пропорционально количеству успешных проверок:

function trace(canvas) {
  var ctx = canvas.getContext("2d");
  var w = canvas.width;
  var h = canvas.height;
  var img = ctx.createImageData(w, h);
  var n = 2;
  for(var x=0; x<w; x++)
    for(var y=0; y<h; y++)
    {
      var k=0;
      for(var xx=0; xx<n; xx++)
        for(var yy=0; yy<n; yy++)
          if(check(x+xx/n, y+yy/n)) k++;
      if(k) img.data[(y*w+x)*4+3]=255*k/n/n;
    }
  ctx.putImageData(img, 0, 0);
}

Результат получается такой:

Уже вполне красиво. Кому мало, можно увеличить значение n (разумеется, считать будет медленнее).

Вернёмся к исходной задаче. По сути дела нам нужно написать характеристическую функцию для диаграммы разложения числа на простые множители. Я немного поменяю прототип функции, чтобы передать все нужные параметры задачи и воспользоваться рекурсией. Функция check будет принимать аргументы (factors, n, x, y, r), где x и y координаты точки относительно центра окружности, r — радиус окружности, factors — массив простых множителей, где двойки уже объединены в четвёрки, как это делал helarqjsc, а n — элемент массива, с которого нам нужно начинать рассмотрение. Тогда функция check будет выглядеть примерно так:
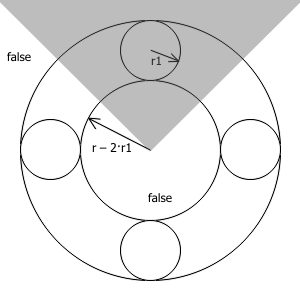— Если расстояние от центра до текущей точки больше радиуса, точка точно не подходит — вернём false;
— Если n указывает на конец массива, значит мы добрались до конца и надо просто рисовать закрашенный кружок — вернём true;
— Иначе вычислим радиус окружности следующего порядка (r1);
— Если расстояние от центра до текущей точки меньше радиуса за вычетом диаметра новой окружности (2*r1), то точка попадает внутрь кольца — вернём false;
— Вычислим сектор, в который попадает точка (серым цветом на картинке);
— Вызовем саму себя с тем же factors, на единицу большим n, новым радиусом r1 и значениями x и y, откорректированными в соответствии с центром новой окружности.

Вот, собственно, и всё. Готовое приложение на JS вы можете видеть здесь (требуется поддержка canvas в браузере, никаких fallback для IE 6-8 нету). Я использовал функции helarqjsc для разложения на простые множители, а рендеринг полностью мой. Картинки у меня немного другие, потому что радиусы окружностей и расположение секторов я вычислял по-другому. Можно заметить, что скорость отрисовки практически не зависит от вводимого числа. Хотя реализация helarqjsc быстрее для первой сотни, но дальше моя начинает выигрывать (для честности я тоже не кэшировал значения синусов и косинусов). Использованный мной подход позволяет упростить и ускорить визуализацию многих нетривиальных вещей. Особенно он полезен при рендеринге фракталов. Заметьте также, что при моём подходе очень легко добавить неограниченный зум в любой области рисунка.

Автор: lany