WebGL существует уже давно, про шейдеры написано немало статей, есть серии уроков. Но в основной массе они слишком сложные для верстальщика. Даже лучше сказать, что они охватывают большие объемы информации, которые скорее нужны разработчику игрового движка, чем верстальщику. Там сразу начинают с построения сложной сцены, камера, свет… На обычном сайте для создания пары эффектов с фотографиями все эти знания избыточны. В результате люди делают очень сложные архитектурные конструкции и пишут длинные-длинные шейдеры ради очень простых по сути действий.
Все это побудило создать введение в те аспекты работы с шейдерами, которые наиболее вероятно пригодятся в работе именно верстальщику для создания различных 2d-эффектов с картинками на сайте. Конечно с поправкой на то, что сами по себе в дизайне интерфейсов они у нас применяются относительно редко. Мы сделаем стартовый шаблон на чистом JS без сторонних библиотек и рассмотрим идеи создания некоторых популярных эффектов, основанных на сдвиге пикселей, которые сложно сделать на SVG, но при этом они легко реализуются с помощью шейдеров.
Предполагается, что читатель уже знаком с
canvas, в общих чертах представляет, что такое WebGL, и владеет минимальными познаниями в математике. Некоторые моменты будут описаны упрощенно, не академично, с целью дать практическое понимание технологий для работы с ними, а не полную теорию их внутренней кухни или термины для вызубривания. Для этого есть умные книжки.
Сразу стоит отметить, что интегрированные в статью редакторы от CodePen имеют свойство влиять на производительность того, что в них выполняется. Так что прежде, чем писать комментарий, что у вас на макбуке что-то тормозит — убедитесь, что проблема исходит не от них.
Основные идеи
Что такое шейдер?
Что такое фрагментный шейдер? По сути, это — маленькая программа. Она выполняется для каждого пикселя на сanvas. Если у нас есть canvas размером 1000x500px, то эта программа выполнится 500000 раз, каждый раз получая в качестве своих входных параметров координаты пикселя, для которого она выполняется в данный момент. Это все происходит на GPU во множестве параллельных потоков. На центральном процессоре подобные вычисления занимали бы гораздо больше времени.
Вершинный шейдер — это тоже программа, но он выполняется не для каждого пикселя на canvas, а для каждой вершины в фигурах, из которых у нас все строится в трехмерном пространстве. Также параллельно для всех вершин. Соответственно получает на вход координаты вершины, а не пикселя.
Дальше в контексте нашей задачи происходит следующее:
- Мы берем набор координат вершин прямоугольника, на котором потом будет "нарисована" фотография.
- Вершинный шейдер для каждой вершины считает ее расположение в пространстве. У нас это будет сводиться к частному случаю — плоскости, параллельной экрану. Фотографии в 3d нам не нужны. Последующая проекция на плоскость экрана можно сказать ничего не делает.
- Дальше для каждого видимого фрагмента, а в нашем контексте для всех фрагментов-пикселей, выполняется фрагментный шейдер, он берет фотографию и текущие координаты, что-то считает и выдает цвет для этого конкретного пикселя.
- Если во фрагментном шейдере не было никакой логики, то поведение всего этого будет напоминать метод
drawImage()уcanvas. Но потом мы добавим эту самую логику и получим много всего интересного.
Это сильно упрощенное описание, но должно быть понятно, кто что делает.
Немного про синтаксис
Шейдеры пишутся на языке GLSL — OpenGL Shading Language. Этот язык очень похож на Си. Описывать здесь весь синтасис и стандартные методы не имеет смысла, но вы всегда можете воспользоваться шпаргалкой:

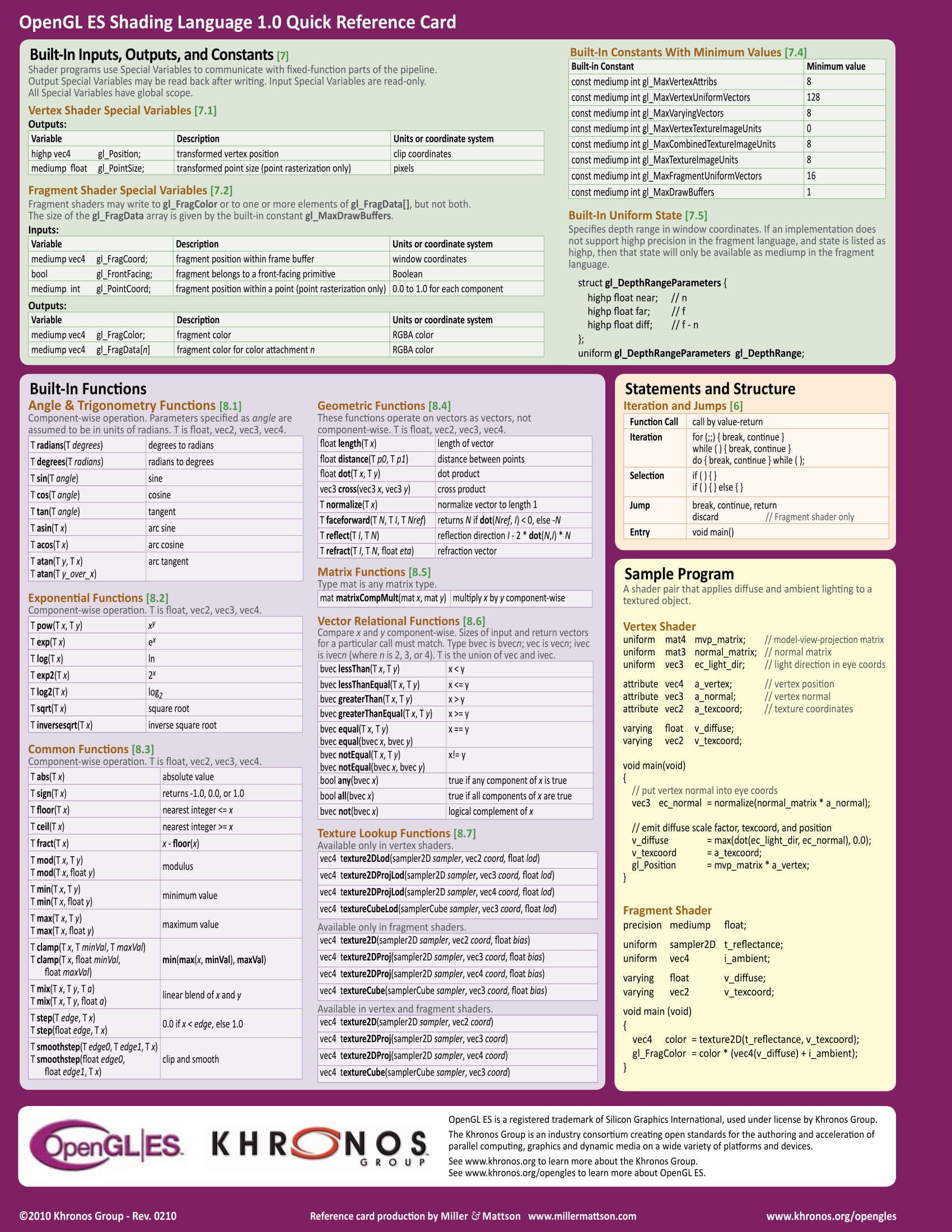


Каждый шейдер имеет функцию main, с которой начинается его выполнение. Стандартные входные параметры для шейдеров и вывод результатов их работы реализуются через специальные переменные с приставкой gl_. Они зарезервированы заранее и доступны внутри этих самых шейдеров. Так координаты вершины для вершинного шейдера лежат в переменной gl_Position, координаты фрагмента (пикселя) для фрагментного шейдера лежат в gl_FragCoord и.т.д. Полный список доступных специальных переменных вы всегда найдете в той же шпаргалке.
Основные типы переменных в GLSL достаточно незатейливы — void, bool, int, float… Если вы работали с каким-нибудь Си-подобным языком, вы их уже видели. Есть и другие типы, в частности векторы разных размерностей — vec2, vec3, vec4. Мы будем постоянно использовать их для координат и цветов. Сами переменные, которые мы можем создавать, бывают трех важных модификаций:
- Uniform — Глобальные во всех смыслах данные. Передаются извне, одинаковы для всех вызовов вершинных и фрагментных шейдеров.
- Attribute — Эти данные передаются уже более точечно и для каждого вызова шейдера могут быть разными.
- Varying — Нужны для передачи данных от вершинных шейдеров во фрагментные.
Полезно делать префиксы u/a/v ко всем переменным в шейдерах, чтобы упростить понимание того, какие данные откуда взялись.
Полагаю, что стоит перейти к практическому примеру, чтобы сразу смотреть все это в действии и не загружать свою память.
Готовим стартовый шаблон
Начнем с JS. Как это обычно и бывает при работе с canvas, нам нужен он сам и контекст. Чтобы не загружать код примеров, сделаем глобальные переменные:
const CANVAS = document.getElementById(IDs.canvas);
const GL = canvas.getContext('webgl');Пропустим момент, связанный с размером canvas и его перерасчетом при изменении размера окна браузера. Этот код включен в примеры и обычно зависит от остальной верстки. Нет смысла акцентировать на нем внимание. Перейдем сразу к действиям с WebGL.
function createProgram() {
const shaders = getShaders();
PROGRAM = GL.createProgram();
GL.attachShader(PROGRAM, shaders.vertex);
GL.attachShader(PROGRAM, shaders.fragment);
GL.linkProgram(PROGRAM);
GL.useProgram(PROGRAM);
}Сначала мы компилируем шейдеры (будет немного ниже), создаем программу, добавляем в нее оба наших шейдера и производим линковку. На этом этапе проверяется совместимость шейдеров. Помните про varying-переменные, которые передаются от вершинного во фрагментный? — Вот в частности их наборы здесь проверяются, чтобы потом в процессе не оказалось, что что-то не передали или передали, но совсем не то. Конечно, логические ошибки данная проверка не выявит, думаю это понятно.
Координаты вершин будут храниться в специальном массиве-буфере и будут по кусочкам, по одной вершине, передаваться в каждый вызов шейдера. Далее мы описываем некоторые детали для работы с этими кусочками. Во-первых, координаты вершины в шейдере мы будем использовать через переменную-атрибут a_position. Можно по-другому назвать, не важно. Получаем ее расположение (это что-то вроде указателя в Си, но не указатель, а скорее номер сущности, существующий только в рамках программы).
const vertexPositionAttribute = GL.getAttribLocation(PROGRAM, 'a_position');Далее мы указываем, что через эту переменную будет передаваться массив с координатами (в самом шейдере мы его будем воспринимать уже как вектор). WebGL самостоятельно разберется с тем, какие именно координаты каких точек в наших фигурах передавать в какой вызов шейдера. Мы только задаем параметры для массива-вектора, который будет передаваться: размерность — 2 (будем передавать координаты (x,y)), он состоит из чисел и не нормализован. Последние параметры нам не интересны, оставляем нули по умолчанию.
GL.enableVertexAttribArray(vertexPositionAttribute);
GL.vertexAttribPointer(vertexPositionAttribute, 2, GL.FLOAT, false, 0, 0);Теперь создадим сам буфер с координатами вершин нашей плоскости, на которой потом будет отображаться фотография. Координаты "в 2d" понятнее, а для наших задач это самое главное.
function createPlane() {
GL.bindBuffer(GL.ARRAY_BUFFER, GL.createBuffer());
GL.bufferData(
GL.ARRAY_BUFFER,
new Float32Array([
-1, -1,
-1, 1,
1, -1,
1, 1
]),
GL.STATIC_DRAW
);
}Этого квадрата будет достаточно для всех наших примеров. STATIC_DRAW означает, что буфер загружается один раз и потом будет переиспользоваться. Повторно мы ничего загружать не будем.
Перед тем, как перейти к самим шейдерам, посмотрим на их компиляцию:
function getShaders() {
return {
vertex: compileShader(
GL.VERTEX_SHADER,
document.getElementById(IDs.shaders.vertex).textContent
),
fragment: compileShader(
GL.FRAGMENT_SHADER,
document.getElementById(IDs.shaders.fragment).textContent
)
};
}
function compileShader(type, source) {
const shader = GL.createShader(type);
GL.shaderSource(shader, source);
GL.compileShader(shader);
return shader;
}Получаем код шейдеров из элементов на странице, создаем шейдер и компилируем его. По идее можно хранить код шейдеров в отдельных файлах и подгружать его во время сборки в виде строки в нужном месте, но CodePen не предоставляет такой возможности для примеров. Во многих уроках предлагается писать код прямо в строке в JS, но назвать это удобным язык не поворачивается. Хотя конечно на вкус и цвет...
Если при компиляции произойдет ошибка, скрипт продолжит выполнение показав пару предупреждений в консоли, которые не несут особого смысла. Полезно после компиляции посмотреть логи чтобы не ломать голову над тем, что же там не скомпилировалось:
console.log(GL.getShaderInfoLog(shader));WebGL предоставляет несколько разных вариантов отслеживания проблем при компиляции шейдеров и создании программы, но на практике получается, что в реальном времени мы все равно починить ничего не можем. Так что часто мы будем руководствоваться мыслью "отвалилось — значит отвалилось" и не будем загружать код кучей лишних проверок.
Переходим к самим шейдерам
Поскольку у нас будет всего одна плоскость, с которой мы ничего делать не собираемся, нам хватит и одного простого вершинного шейдера, который и сделаем в самом начале. Основные усилия будут сосредоточены на фрагментных шейдерах и все последующие примеры будут иметь отношение к ним.
Старайтесь писать код шейдеров с более-менее осмысленными названиями переменных. В сети вы встретите примеры, где из однобуквенных переменных будут собираться функции с ядреной математикой на 200 строк сплошного текста, но то, что кто-то так делает, еще не значит, что это стоит повторять. Подобный подход — это не "специфика работы с GL", это — банальная копипаста исходников еще из прошлого века, написанных людьми, которые в молодости имели ограничения на длину имен переменных.
Для начала вершинный шейдер. В переменную-атрибут a_position будет передаваться 2d-вектор с координатами (x,y), как мы и говорили. Шейдер должен вернуть вектор из четырех значений (x,y,z,w). Перемещать в пространстве он ничего не будет, так что по оси z просто все обнуляем и ставим значение w в стандартную единицу. Если вам интересно, почему координат четыре, а не три, то вы можете воспользоваться поиском в сети по запросу "однородные координаты".
<script id='vertex-shader' type='x-shader/x-vertex'>
precision mediump float;
attribute vec2 a_position;
void main() {
gl_Position = vec4(position, 0, 1);
}
</script>Результат работы записывается в специальную переменную gl_Position. У шейдеров нет оператора return в полном смысле этого слова, все результаты своей работы они записывают в специально зарезервированные для этих целей переменные.
Обратите внимание на задание точности для типа данных float. Чтобы избежать некоторой части проблем на мобильных устройствах, точность должна быть хуже, чем highp и должна быть одинаковой в обоих шейдерах. Здесь это показано для примера, но хорошей практикой будет на телефонах подобную красоту с шейдерами совсем отключать.
Фрагментный шейдер для начала будет возвращать всегда один и тот же цвет. Наш квадрат будет занимать весь canvas, так что по факту здесь мы задаем цвет каждому пикселю:
<script id='fragment-shader' type='x-shader/x-fragment'>
precision mediump float;
#define GOLD vec4(1.0, 0.86, 0.6, 1.0)
void main() {
gl_FragColor = GOLD;
}
</script>Вы можете обратить внимание на числа, описывающие цвет. Это знакомый всем верстальщикам RGBA, только нормализованный. Значения не целые от 0 до 255, а дробные от 0 до 1. Порядок тот же.
Не забывайте использовать препроцессор для всех магических констант в реальных проектах — это делает код более понятным не оказывая влияния на производительность (подстановка, также как и в Си, происходит при компиляции).
Стоит отметить еще один момент о препроцессоре:
Использование постоянных проверок #ifdef GL_ES в различных уроках лишено практического смысла, т.к. у нас в браузере на сегодняшний день никаких других вариантов GL просто не существует.
Но пора бы уже посмотреть на результат:
Золотой квадрат говорит о том, что шейдеры работают как положено. Имеет смысл немного поиграться с ними, перед тем, как перейти к работе с фотографиями.
Градиент и преобразования векторов
Обычно в уроках по WebGL начинают с рисования градиентов. Это имеет мало практического смысла, но будет полезно отметить пару моментов.
void main() {
gl_FragColor = vec4(gl_FragCoord.zxy / 500.0, 1.0);
}В этом примере мы используем координаты текущего пикселя в качестве цвета. Вы часто будете такое встречать в примерах в сети. И то и другое — векторы. Так что никто не мешает все смешать в кучу. У евангелистов TypeScript здесь должен случиться приступ. Важным моментом является то, как мы достаем из вектора только часть координат. Свойства .x, .y, .z, .xy, .zy, .xyz, .zyx, .xyzw и.т.д. в разных последовательностях позволяют вытащить элементы вектора в определенном порядке в виде другого вектора. Очень удобно реализовано. Также вектор большей размерности можно сделать из вектора меньшей размерности, добавив недостающие значения, как мы и поступили.
Всегда явно указывайте дробную часть чисел. Автоматического преобразования int -> float здесь нет.
Uniforms и ход времени
Следующий полезный пример — использование uniforms. Это те самые общие для всех вызовов шейдеров данные. Мы получаем их расположение почти тем же образом, что и для переменных-атрибутов, например:
GL.getUniformLocation(PROGRAM, 'u_time')Потом мы можем устанавливать им значения перед каждым кадром. Также, как и с векторами, здесь есть много похожих методов, начинающихся со слова uniform, далее идет размерность переменной (1 для чисел, 2, 3 или 4 для векторов) и тип (f — float, i — int, v — вектор).
function draw(timeStamp) {
GL.uniform1f(GL.getUniformLocation(PROGRAM, 'u_time'), timeStamp / 1000.0);
GL.drawArrays(GL.TRIANGLE_STRIP, 0, 4);
window.requestAnimationFrame(draw);
}На самом деле нам не всегда нужны 60fps в интерфейсах. Вполне можно добавить тормозилку к requestAnimationFrame и снизить частоту перерисовки кадров.
Для примера будем изменять цвет заливки. В шейдерах доступны все основные математические функции — sin, cos, tan, asin, acos, atan, pow, exp, log, sqrt, abs и другие. Воспользуемся двумя из них.
uniform float u_time;
void main() {
gl_FragColor = vec4(
abs(sin(u_time)),
abs(sin(u_time * 3.0)),
abs(sin(u_time * 5.0)), 1.0);
} Время в таких анимациях — понятие относительное. Здесь мы используем те значения, которые предоставляет нам requestAnimationFrame, но можем сделать свое "время". Идея в том, что если какие-то параметры описываются функцией от времени, то мы можем повернуть время в обратную сторону, замедлить, ускорить его или вернуться в исходное состояние. Это бывает очень полезно.
Но хватит абстрактных примеров, перейдем к использованию картинок.
Загружаем картинку в текстуру
Для того, чтобы использовать картинку, нам нужно создать текстуру, которая потом будет отрендерена на нашей плоскости. Для начала загружаем само изображение:
function createTexture() {
const image = new Image();
image.crossOrigin = 'anonymous';
image.onload = () => {
// ....
};
image.src = 'example.jpg';
}После того, как оно загрузится, создаем текстуру и указываем, что она будет идти под номером 0. В WebGL одновременно может существовать много текстур и мы должны явно указать, к какой будут относиться последующие команды. В наших примерах будет только одна текстура, но мы все равно явно указываем, что она будет нулевой.
const texture = GL.createTexture();
GL.activeTexture(GL.TEXTURE0);
GL.bindTexture(GL.TEXTURE_2D, texture);Остается добавить картинку. Также мы сразу говорим, что ее нужно перевернуть по оси Y, т.к. в WebGL ось перевернута:
GL.pixelStorei(GL.UNPACK_FLIP_Y_WEBGL, true);
GL.texImage2D(GL.TEXTURE_2D, 0, GL.RGB, GL.RGB, GL.UNSIGNED_BYTE, image);По идее текстуры должны быть квадратными. Точнее даже должны иметь размер, равный степени двойки — 32px, 64px, 128px и.т.д. Но все мы понимаем, что фотографии никто обрабатывать не станет и они будут каждый раз разных пропорций. Это будет вызывать ошибки даже если canvas по размеру идеально подходит к текстуре. Поэтому мы заполняем все пространство до краев плоскости крайними пикселями изображения. Это стандартная практика, хотя и кажется немного костыльной.
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_S, GL.CLAMP_TO_EDGE);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_WRAP_T, GL.CLAMP_TO_EDGE);
GL.texParameteri(GL.TEXTURE_2D, GL.TEXTURE_MIN_FILTER, GL.LINEAR);Остается передать текстуру в шейдеры. Это общие для всех данные, так что используем модификатор uniform.
GL.uniform1i(GL.getUniformLocation(PROGRAM, 'u_texture'), 0);Теперь мы можем использовать цвета из текстуры во фрагментном шейдере. Но мы также хотим, чтобы картинка занимала весь canvas. Если изображение и canvas имеют одинаковые пропорции, то эта задача становится тривиальной. Для начала передаем размер canvas в шейдеры (это нужно делать каждый раз при изменении его размера):
GL.uniform1f(GL.getUniformLocation(PROGRAM, 'u_canvas_size'),
Math.max(CANVAS.height, CANVAS.width));И делим на него координаты:
uniform sampler2D u_texture;
uniform float u_canvas_size;
void main() {
gl_FragColor = texture2D(u_texture, gl_FragCoord.xy / u_canvas_size);
} На этом моменте можно сделать небольшую паузу и заварить чаю. Мы проделали всю подготовительную работу и переходим к созданию различных эффектов.
Эффекты
При создании различных эффектов важную роль играет интуиция и эксперименты. Часто можно заменить сложный алгоритм чем-то совершенно простым и дающим похожий результат. Конечный пользователь разницы не заметит, а мы ускоряем работу и упрощаем поддержку. WebGL не предоставляет толковых инструментов для отладки шейдеров, так что нам выгодно иметь небольшие куски кода, которые могут уместиться в голове целиком.
Меньше кода — меньше проблем. И читать проще. Всегда проверяйте шейдеры, найденные в сети, на предмет лишних действий. Бывает, что можно половину кода удалить и ничего не изменится.
Немного поиграем с шейдером. Большинство наших эффектов будут строиться на том, что мы возвращаем цвет не того пикселя на текстуре, который должен быть в этом месте, а какой-то из соседних. Полезно попробовать добавлять к координатам результат выполнения какой-либо стандартной функции от координат. Время также будет полезно использовать — так результат выполнения будет проще отслеживать, да и в конечном счете мы все равно будем делать анимированные эффекты. Попробуем поиспользовать синус:
gl_FragColor = texture2D(u_texture, gl_FragCoord.xy / u_canvas_size
+ sin(u_time + gl_FragCoord.y));Результат странный. Очевидно, что все движется со слишком большой амплитудой. Поделим все на какое-нибудь число:
gl_FragColor = texture2D(u_texture, gl_FragCoord.xy / u_canvas_size
+ sin(u_time + gl_FragCoord.y) / 250.0);Уже лучше. Теперь понятно, что получилось небольшое волнение. По идее, чтобы увеличить каждую волну нам нужно поделить аргумент синуса — координату. Сделаем это:
gl_FragColor = texture2D(u_texture, gl_FragCoord.xy / u_canvas_size
+ sin(u_time + gl_FragCoord.y / 30.0) / 250.0);Подобные эффекты часто сопровождаются подбиранием коэффициентов. Это делается на глазок. Как и с кулинарией, поначалу будет сложно угадывать, но потом это будет происходить само собой. Главное — хотя бы примерно понимать, на что влияет тот или иной коэффициент в получившейся формуле. После того, как коэффициенты подобраны, имеет смысл выносить их в макросы (как это было в первом примере) и давать осмысленные имена.
Кривое зеркало, велосипеды и эксперименты
Думать полезно. Да, есть готовые алгоритмы решения некоторых задач, которые мы можем просто так брать и использовать. Но в процессе придумывания мы познаем идеи, которые так бы прошли мимо нас.
Возможно мы не хотим делать такие равномерные горизонтальные волны, а хотим "кривое зеркало", в котором все будет искажаться случайным образом. Что же делать?
Кажется, что нам будет нужна генерация случайных чисел, не так ли? Раз уж все должно быть случайным. Но вот незадача, у нас здесь нет стандартной функции rand() или чего-то похожего. Все дело в том, что она реализуется так, что следующий результат, следующее число, зависит от предыдущего. Получается последовательность случайных чисел. Но шейдеры выполняются параллельно и мы не можем передавать последовательность от одного к другому без вреда для производительности. Но если подумать, то нам это и не нужно. Нам нужно генерировать случайное число в зависимости от координат. То есть нам нужна урезанная реализация. Это даже скорее хеш-функция, чем генератор случайных чисел. Алгоритмов хеширования придумали уже достаточно много. Нам желательно иметь такой, чтобы принимал на вход координаты, чтобы самим не делать обертку над ним, и выдавал число. Есть готовый вариант этой функции, который уже очень давно кочует по интернету и многими называется "каноническим":
float rand(vec2 seed) {
return fract(sin(dot(seed, vec2(12.9898,78.233))) * 43758.5453123);
}
Одни умные люди говорят, что распределение случайных чисел у нее далеко не самое лучшее, другие, что реализация функции синуса у NVIDIA и ATI отличаются и результаты будут непредсказуемыми. Все это важно для криптографии, а нам короткий однострочник вполне может и сгодиться.
Если мы просто так добавим случайный компонент, то получится нечто странное, поэтому сразу поделим на коэффициент для уменьшения амплитуды нашего рандома:
gl_FragColor = texture2D(u_texture,
gl_FragCoord.xy / u_canvas_size
+ rand(gl_FragCoord.xy) / 100.0);И вернуть сюда функцию от времени тоже будет не лишним:
gl_FragColor = texture2D(u_texture,
gl_FragCoord.xy / u_canvas_size
+ rand(gl_FragCoord.xy + vec2(sin(u_time))) / 250.0);Получилось не совсем то, что нам нужно, но тоже занятно:
Очевидно, что в целом мы двигаемся в том направлении. Только сейчас анимируются отдельные пиксели, а нам нужно, чтобы двигались целые куски изображения. Первая мысль — поделить изображение на квадраты и применять трансформации к каждому по отдельности. Как это сделать? Округлением. Похожая фишка используется в блочной сортировке.
Поскольку у нас используются координаты от 0 до 1, нужно умножить их на какой-нибудь коэффициент. В данном случае 5 — это и будет количеством квадратов в одной линии в анимации. Также вынесем в отдельную переменную наши координаты, чтобы они не рассчитывались несколько раз.
vec2 texture_coord = gl_FragCoord.xy / u_canvas_size;
gl_FragColor = texture2D(u_texture,
texture_coord
+ rand(floor(texture_coord * 5.0) + vec2(sin(u_time))) / 100.0);Получатся просто квадраты, которые двигаются туда-сюда и рвут все изображение. Нам нужно как-то сгладить все это. Сделать, чтобы сдвиги менялись плавно, без выраженных границ. Как мы можем это сделать?
Мы можем рассчитать значения сдвига для отдельных точек, а все, что между ними, выразить какой-нибудь функцией. Это так и называется интерполяция, сглаживание. В данном случае билинейная, т.к. у нас функции от двух переменных-координат. Пусть этими точками будут вершины квадратов, на которые мы поделили все изображение. Вынесем часть логики в отдельную функцию. То, что у нас получится в итоге из этой функции, называется генератором шума. Вы будете иногда встречать его в различных эффектах.
Добавим также отдельно sin и cos для разных координат, чтобы немного рассинхронизировать анимацию. Такое часто делают. Будет полезно поиграть и с другими функциями и коэффициентами.
gl_FragColor = texture2D(u_texture,
texture_coord
+ vec2(
noise(texture_coord * 10.0 + sin(u_time + texture_coord.x * 5.0)) / 10.0,
noise(texture_coord * 10.0 + cos(u_time + texture_coord.y * 5.0)) / 10.0));Для начала пусть все будет линейным. Используем функцию fract как есть. Блоки будут размера 1 на 1 — мы округляем до целых чисел:
float noise(vec2 position) {
vec2 block_position = floor(position);
float top_left_value = rand(block_position);
float top_right_value = rand(block_position + vec2(1.0, 0.0));
float bottom_left_value = rand(block_position + vec2(0.0, 1.0));
float bottom_right_value = rand(block_position + vec2(1.0, 1.0));
vec2 computed_value = fract(position);
// ...
}Мы можем попробовать использовать другую функцию для интерполяции. WebGL в частности предоставляет нам функцию smoothstep, она даст более плавные движения:
vec2 computed_value = smoothstep(0.0, 1.0, fract(position));Возникает вопрос о том, какое значение вернуть из этой функции. Алгоритм интерполяции известен, но давайте в качестве эксперимента попробуем вернуть координату по X у полученного значения:
return computed_value.x;Ооо… Ни разу не то, что нужно, но зато как красиво...
Полезно иногда сделать что-нибудь странное, поменять знаки в известных алгоритмах, вернуть только часть результатов и.т.д. и заодно набраться идей для решения других задач.
Если возвращать значение по y — будет то же самое, но по горизонтали. А что если вернуть длину вектора?
return length(computed_value);Тоже очень даже интересная штука.
Но вернемся к известному алгоритму. Для удобства сразу вычитаем 0.5 — пусть будут и отрицательные значения тоже.
return mix(top_left_value, top_right_value, computed_value.x)
+ (bottom_left_value - top_left_value) * computed_value.y * (1.0 - computed_value.x)
+ (bottom_right_value - top_right_value) * computed_value.x * computed_value.y
- 0.5;На этот результат точно стоит посмотреть:
Тут можно сделать еще одну паузу, поиграть с коэффициентами, посмотреть, что будет.
Отменяем эффект
Поскольку мы делаем эффекты не просто в вакууме, а для использования в интерфейсах, было бы неплохо добавить возможность возвращать все к исходной картинке. И применять эффект при наведении мыши или еще каком-нибудь событии.
Проще всего добавить uniform-переменную, которая будет отвечать за силу применения трансформаций. Скажем от 0 до 1, где 0 — ничего не происходит, а 1 — трансформируется все.
uniform float u_intensity;Мы можем умножать на нее вектор трансформации:
gl_FragColor = texture2D(u_texture,
texture_coord
+ vec2(noise(texture_coord * 10.0 + sin(u_time + texture_coord.x * 5.0)) / 10.0,
noise(texture_coord * 10.0 + cos(u_time + texture_coord.y * 5.0)) / 10.0)
* u_intensity);Для примера будем плавно менять интенсивность при наведении мыши, отключая тем самым эффект с искажениями.
Если совместить этот процесс с изменением прозрачности цвета (также от 0 до 1), то можно делать красивые растворения изображений при переходе к новому слайду в галерее.
После того, как эффект полностью отменен, имеет смысл прекращать перерисовку каждого кадра до тех пор, пока не будет нужно активировать эффект снова. Если у вас на странице одновременно перерисовываются несколько элементов — старайтесь все их собрать в один цикл с requestAnimationFrame. Чем больше этих циклов будет на странице, тем сильнее будет проседать FPS.
Увеличительное стекло и мышка
И раз уж заговорили про мышку, будет не лишним передать в шейдер ее положение. Также через uniform-переменную.
document.addEventListener('mousemove', (e) => {
let rect = CANVAS.getBoundingClientRect();
MOUSE_POSITION = [
e.clientX - rect.left,
rect.height - (e.clientY - rect.top)
];
GL.uniform2fv(GL.getUniformLocation(PROGRAM, 'u_mouse_position'), MOUSE_POSITION);
});И попробуем использовать сдвиг, основываясь на направлении и длине вектора из текущего положения в положение мыши. Если расстояние не очень большое — применяем трансформацию, а все остальное пусть остается как есть.
void main() {
vec2 texture_coord = gl_FragCoord.xy / u_canvas_size;
vec2 direction = u_mouse_position / u_canvas_size - texture_coord;
float dist = distance(gl_FragCoord.xy, u_mouse_position) / u_canvas_size;
if (dist < 0.4) {
gl_FragColor = texture2D(u_texture,
texture_coord
+ u_intensity * direction * dist * 1.2
);
} else {
gl_FragColor = texture2D(u_texture, texture_coord);
}
} Читателю будет полезно поиграть с коэффициентами и использовать какую-нибудь нелинейную функцию от расстояния. Таким образом можно будет получить вогнутую или выпуклую линзу.
Узнайте как ведут себя все стандартные математические функции по отдельности и при сложении. Это даст понимание того, какие именно функции дадут тот или иной результат.
Помехи
Напоследок посмотрим еще одну популярную штуку. Glitch-эффект можно делать тысячей разных способов, в том числе и на SVG. Но там его сложно сделать производительным. А на шейдерах — напротив. Что из себя представляет данный эффект? В целом здесь нет ничего сложного — горизонтальные полосы, некоторые из них, выбранные случайным образом, сдвигаются на случайную величину по горизонтали.
float random_value = rand(vec2(texture_coord.y, u_time));
if (random_value < 0.05) {
gl_FragColor = texture2D(u_texture,
vec2(texture_coord.x + random_value / 5.0,
texture_coord.y));
} else {
gl_FragColor = texture2D(u_texture, texture_coord);
}"Что из себя представляет данный эффект?" — Это важный вопрос, который начинающие часто забывают себе задать. И это приводит к ступору даже с такими простыми задачами.
Можно также увеличить ширину полос. Действуем по уже знакомому сценарию — умножаем координаты, округляем и производим одни и те же вычисления для множества точек.
float random_value = rand(vec2(floor(texture_coord.y * 20.0), u_time));Можем также поиграть с цветом. Например поменять яркость, добавляя случайное значение ко всем каналам цвета:
gl_FragColor = texture2D(u_texture,
vec2(texture_coord.x + random_value / 4.0,
texture_coord.y))
+ vec4(vec3(random_value), 1.0);На фоне предыдущих примеров этот уже не должен казаться сложным. Игры с отдельными компонентами цвета оставим в качестве упражнения — здесь можно долго экспериментировать. Удобно, что из вектора отдельные цветовые каналы можно доставать аналогично координатам — есть свойства .r, .g, .b, .rg, .rb, .rgb, .bgr, и.т.д. Использование разных обозначений для цветов и для координат помогает не смешивать все в одну кучу.
Возвращаем параметр интенсивности и смотрим на результат:
float random_value = u_intensity * rand(vec2(floor(texture_coord.y * 20.0), u_time));Что в итоге?
На примере нескольких простых эффектов с фотографиями мы выяснили, что их вполне можно делать без сторонних библиотек и что шейдеры могут быть короткими и вполне доступными для понимания, если их намеренно не усложнять. Многие популярные эффекты базируются на смещении пикселей по определенным формулам, и все, что нужно для их написания — это немного пространственного воображения и базовые знания по математике.
Автор: sfi0zy