Профессор математики Опиеми Энох (Opeyemi Enoch) из Нигерии заявил о том, что он смог решить одну из семи математических «проблем тысячелетия». Речь идет о так называемой гипотезе Римана, над доказательством которой математики со всего мира работают вот уже 150 лет. Как говорит нам Википедия, гипотеза Римана о распределении нулей дзета-функции Римана была сформулирована Бернхардом Риманом в 1859 году. В то время как не найдено какой-либо закономерности, описывающей распределение простых чисел среди натуральных, Риман обнаружил, что количество простых чисел, не превосходящих 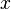 , — функция распределения простых чисел, обозначаемая
, — функция распределения простых чисел, обозначаемая 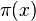 — выражается через распределение так называемых «нетривиальных нулей» дзета-функции. Многие утверждения о распределении простых чисел, в том числе о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности гипотезы Римана.
— выражается через распределение так называемых «нетривиальных нулей» дзета-функции. Многие утверждения о распределении простых чисел, в том числе о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности гипотезы Римана.
Гипотеза Римана входит в список семи математических «проблем тысячелетия». За решение каждой из них Математический институт Клэя (Clay Mathematics Institute, Кембридж, Массачусетс) обещает выплатить награду в один миллион долларов США. Институт заявляет, что это делается для популяризации математики как науки, и для привлечения новых адептов этой науки из числа молодежи. В случае публикации контрпримера к гипотезе Римана, учёный совет института Клэя вправе решить, можно ли считать данный контрпример окончательным решением проблемы, или же проблема может быть переформулирована в более узкой форме и оставлена открытой (в последнем случае автору контрпримера может быть выплачена небольшая часть награды).
Формулировка гипотезы
Дзета-функция Римана 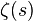 определена для всех комплексных
определена для всех комплексных 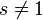 и имеет нули в отрицательных чётных
и имеет нули в отрицательных чётных 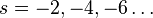 .
.
из функционального уравнения 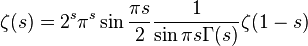 и явного выражения
и явного выражения 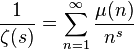 при
при 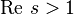 , где
, где 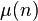 — функция Мёбиуса, следует, что все остальные нули, называемые «нетривиальными», расположены в полосе
— функция Мёбиуса, следует, что все остальные нули, называемые «нетривиальными», расположены в полосе 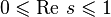 симметрично относительно так называемой «критической линии»
симметрично относительно так называемой «критической линии» 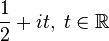 .
.
Свое доказательство гипотезы нигерийский математик представил коллегам в Федеральном университете в городе Ойе-Экити. Пресс-служба этого университета уже подтвердила корректность доказательства. Ранее математик, как сообщает пресс-служба учебного заведения, работал над моделированием систем, позволяющих получать энергию звука, урагана и прибоя.
Nigerian academic solves 150-year old math problem https://t.co/6KYj4wtc2i pic.twitter.com/ZrIOaiQ40F
— This Is Africa (@ThisIsAfricaTIA) 17 ноября 2015
В Математическом институте Клэя пока что считают гипотезу Римана недоказанной. По словам представителей института, для того, чтобы достижение было зафиксировано, его необходимо опубликовать в авторитетном международном журнале, с последующим подтверждением доказательства научным сообществом.
Ранее одну из проблем тысячелетия, гипотезу Пуанкаре, доказал российский математик Григорий Яковлевич Перельман. От награды в миллион долларов он отказался.
Автор: marks