Постановка задачи
На днях я увидел на просторах интернета крайне любопытную вещь: мендосинский двигатель. Ротор на подшипниках крайне низкого трения: оригинальный имел стеклянный цилиндр, подвешенный на двух иголках, современные имеют магнитный подвес оси. Двигатель бесколлекторный, на роторе подвешены солнечные батареи, которые выдают напряжение на катушки, намотанные на роторе. Ротор проворачивается в фиксированном магнитном поле статора, солнечная батарея уходит от направленного света, на её место приходит другая. Крайне элегантное решение, которое вполне под силу сделать дома каждому.
Вот на этом видео крайне подробно описан (на русском языке) принцип работы:
Но ещё больше самого двигателя мне показалась любопытной следующая вещь. В описании этого видео Дмитрий Коржевский написал следующую вещь: «Боковую опору заменить магнитом НЕВОЗМОЖНО!!! Не задавайте больше этот вопрос!»
Отмазка: я ни разу не физик, могу сильно ошибаться, поправки приветствуются.

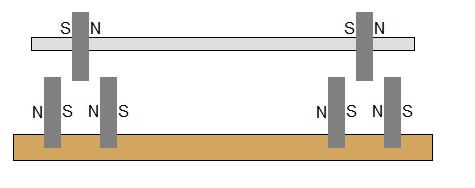
О, это интересно. Давайте ещё раз посмотрим, как работает магнитный подвес ротора. Если мы поставим два магнита, то изолиния потенциала выглядит следующим образом в зависимости от расстояния между двумя магнитами:
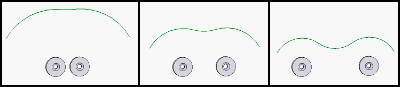
То есть, мы ставим два фиксированных магнита на статоре. Магнит на оси ротора не захочет сдвинуться вбок, т.к. изолиния потенциала имеет некий локальный минимум. Он захочет выскочить вдоль оси ротора. Делаем две таких системы, получаем ось ротора, которая зафиксирована магнитным полем в радиальном направлении, но при этом нестабильна в продольном. Упираем ось в стеклянную стеночку и вуаля, получили подшипник слабого трения.
Но стеклянная стеночка — это как-то… неэлегантно, что ли? Вполне логично желание получить полностью парящий в воздухе ротор, безо всяких костылей. И явно Дмитрия затюкали этим вопросом, да так, что он был вынужден написать невозможность подобного прямо в описании видео. И ведь Дмитрий Коржевский не один такой.
Давайте посмотрим сюда, цитирую:
What would happen if the base magnets were spaced and oriented like in this drawing? Would it give it stability in the axial plane, and do away with the mirror requirement?
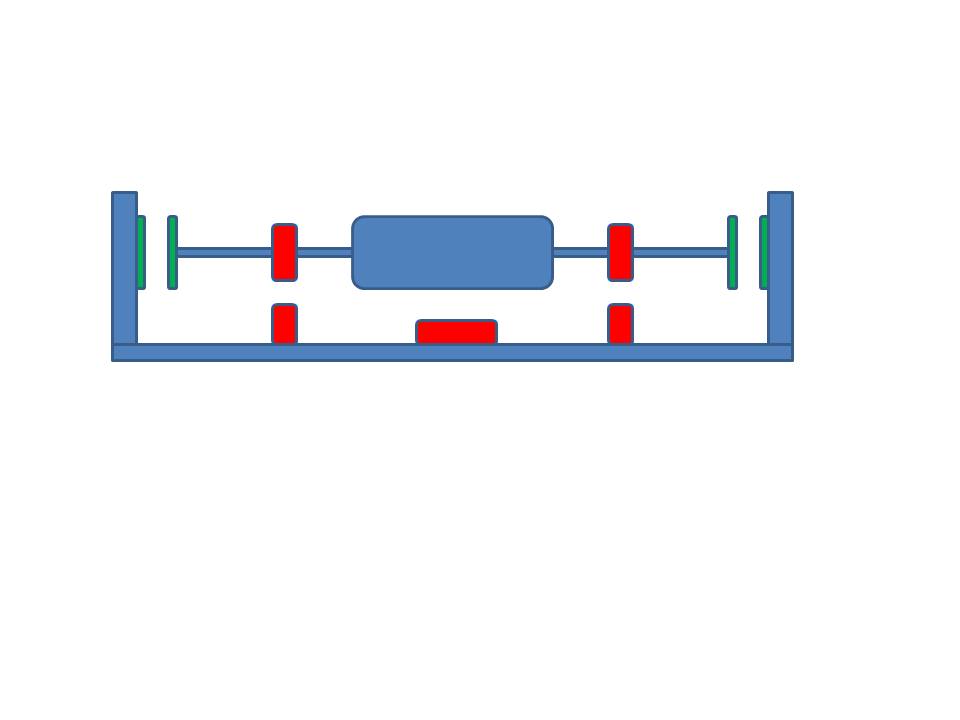
Или сюда, цитирую:
On a Mendocino Motor why does one side float free while the other has a tip to a wall? I know the question might sound trivial but I have worked up the idea why not use the same magnets used to levitate as a counter force on both sides of the shaft? I attached a very rough jpg of what I mean. the green magnets at the end of the shafts is what im referring to. is there some theory or law preventing this?
То есть, люди по всему миру хотят избавиться от механической поддержки оси. Я в школе учился плохо и мне невозможность создания полностью магнитного подвеса без костылей тоже ни разу не очевидна. При случае я за чашкой чая задал своему начальнику, учёному с мировым именем (не физику, прикладному математику), этот вопрос: «А почему, собственно невозможно?» И знаете, ему это тоже не было очевидно!
На вышеозначенных форумах никто толком не объяснил, почему это невозможно. В лучшем случае цитировали какую-то теорему Ирншоу, которая не слишком-то удобоварима. Итак, она гласит следующее: «Всякая равновесная конфигурация точечных зарядов неустойчива, если на них кроме кулоновских сил притяжения и отталкивания ничто не действует.» Вам ясно? Мне нет. Положим, я могу смириться с тем, что мы говорим про заряженные частицы, а не про магниты. Но дальше?
Первая иллюстрация
Когда мне что-то неясно, я рисую картинку. Для простоты она будет в двумерном пространстве. Давайте представим четыре закреплённых единичных заряда по углам квадрата и свободный заряд в центре квадрата. Примерно так:

Неужели свободный заряд не находится в состоянии устойчивого равновесиия? Ведь куда бы он ни двинулся, он приближается к одному из фиксированных зарядов, увеличивая силу отталкивания! Давайте попробуем нарисовать карту потенциальной энергии свободного заряда. Я в школе учился плохо, физику прогуливал, поэтому будем черпать знания из википедии. Итак, если мы имеем в пространстве только один закреплённый заряд, то он создаёт во всём пространстве электростатический потенциал.
Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:
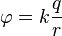
Во всех умозрительных опытах все коэффициенты у меня равны либо нулю, либо единице. Поэтому заряд q единичный, неясный k тоже единица. То есть, один закреплённый заряд создаёт потенциал, измеряемый по формуле 1/r, где r — это расстояние до заряда.
Потенциальная энергия свободного единичного заряда в поле нашего закреплённого заряда также равна 1/r. (Вообще говоря, энергия равна k*q1*q2/r, но коэффициенты выбираем так, чтобы было удобно считать). Для нескольких зарядов все потенциалы просто складываются.
Давайте рисовать карту потенциальной энергии нашего свободного заряда, я это делаю при помощи sage:
var('x,y')
def unit_potential(a,b,x,y): return 1/(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)
Вот карта, я выколол точки, где потенциальная энергия уходит в бесконечность:
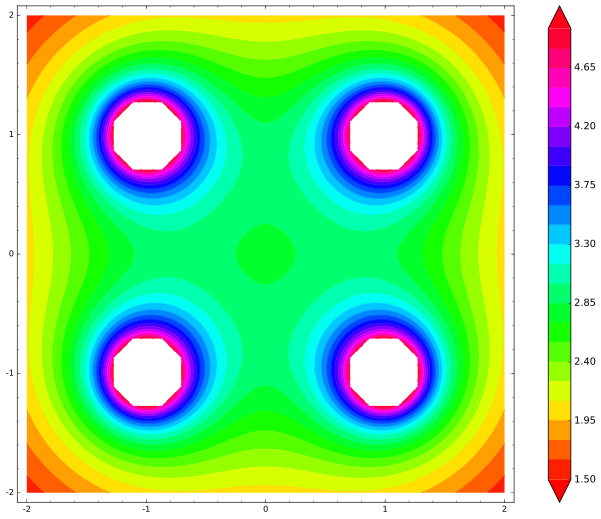
По центру квадрата чётко виден локальный минимум энергии. Куда бы ни двинулась частица из центра, энергия будет увеличиваться, поэтому от небольших возмущений она явно захочет вернуться назад в центр, это точка устойчивого равновесия. Неужели Ирншоу соврал? Нет, он не соврал. Проблема в том, что я плохо нарисовал картинку. И многие ошибаются ровно так же, как и я. Остановитесь сейчас, подумайте, где я ошибся?
В данном случае ошибка в том, что в двумерном пространстве закреплённый заряд создаёт потенциал, измеряемый по формуле -ln r, где r — это расстояние до заряда, а вовсе не 1/r. Давайте на некоторое время вы мне поверите на слово и разрешите неясным образом изменить кулоновскую формулу, тогда корректный код будет выглядеть вот так:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True)
Вот картинка с картой потенциальной энергии:
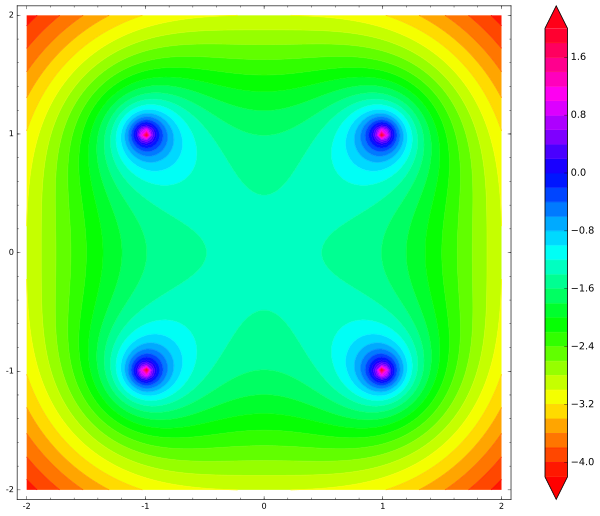
Обратите внимание, что локальных минимумов на карте нет. Центр квадрата — седловая точка, то есть, точка неустойчивого равновесия. Как только свободный заряд сдвинется хоть на микрон от центра квадрата, он обязательно скатится и вылетит из квадрата, ускоряясь и ускоряясь.
Секунду, что всё же произошло с формулой потенциала?
Когда я получил явное противоречие с теоремой Ирншоу, я понял, что где-то прокололся и стал искать ошибку. Ошибку искать лучше всего последовательно с самого начала. Я тяжко вздохнул и пошёл читать, что такое уравнения Максвелла. В школе я учился не то, что бы очень плохо, оценки у меня были отличными. Только знаний вынес явно не по всем предметам. Например, уравнения Максвелла мне разве что в кошмарах снились после школы, а в университете и далее с ними сталкиваться просто не приходилось.
А оказалось, что там всё крайне просто, особенно если мы интересуемся только электростатикой! Уравнений Максвелла четыре по количеству следующих законов:
1. Закон Гаусса, он нам пригодится. Пока оставим всякие дивергенции, «на пальцах» это просто закон сохранения: энергия из ниоткуда не берётся и в никуда не уходит.
2. Закон Гаусса для магнитного поля — те же яйца, вид сбоку. Да и магнитным полем я пока не интересуюсь, т.к. разговор идёт от заряженных частицах, пропускаем.
3. Закон Фарадея: если мы двигаем магнитами, то они порождают электрическое поле, это интересно, подробнее поглядим потом.
4. Закон Ампера: если мы двигаем электрическим полем, то порождаем магнитное. На фиг, неинтересно.
Итак, эти четыре закона связывают между собой два векторных поля E и B, электрическое поле и магнитное. Эти векторные поля — это функции, которые имеют четыре аргумента (x,y,z,t), и каждой четвёрке аргументов сопоставляют один трёхмерный вектор. Магнитное нам не очень интересно в данном случае, рассмотрим поле E(x,y,z,t). Причём не забываем, что мы интересуемся электростатикой, поэтому E постоянно во времени. Очень удобно рассматривать это векторное поле как некоторую реку, где каждой в каждой точке реки мы говорим, куда и с какой скоростью течёт вода.
Закон Фарадея говорит о том, что в случае постоянное во времени поле E (мы же говорим про электростатику) не имеет вихрей.
Как связан электростатический потенциал с электрическим полем? Очень просто: если поле E безвихревое (наш случай), то возможно создать такой ландшафт u, что покрыв его метровым слоем воды (на всех высотах!) и «отпустив» эту воду, скорость и направление течения воды породит поле E. Если умными словами, то можно найти такую скалярную функцию u, что её градиент равен полю E.
Закон Гаусса говорит следующее: возьмём маленькую область пространства. Если мы в неё не поместили заряда специально, то количество
«воды», которое затекает в эту область, равно количеству, которое вытекает. Если хочется выпендриться, то можно сказать, что дивергенция поля E равна нулю.
Напоминаю, что поле E — это производная скалярной функции u. Если её дивергенция равна нулю, то это означает, что лапласиан функции u равен нулю. Лапласиан — это умное слово для обозначения «кривизны» функции. В случае функции одной переменной лапласиан — это просто вторая производная. Вторая производная равна нулю только у постоянной или линейной функции (логично, кривизна равна нулю). В случае функции двух переменных лапласиан — это сумма двух частных производных. Если он равен нулю, то кривизна в одном направлении обязана быть аннулирована кривизной в другом направлении. То есть, чипсы разрешены:

А вот локальных минимумов (максимумов тоже) функция с нулевым лапласианом не имеет. То есть, чипсы разрешены, а холмы нет:

Представьте, что мы обмакнём проволочное колечко (хорошо изогнутое) в мыльную воду. Тогда мыльная плёнка образует поверхность с нулевым лапласианом:

Это будет так называемая минимальная поверхность. Мыльная плёнка старается уменьшить свою площадь. Логично, что если бы на ней был некий локальный максимум, то сгладив его, мы получили бы плёнку меньшей площади. Поэтому их и нет. Итак, электростатический потенциал — это своего рода минимальная поверхность, локальных максимумов (в местах, куда мы специально заряд не помещали) не имеет.
Функция 1/r имеет нулевой лапласиан в трёхмерном пространстве, а вот в двумерном нет! Если мы хотим рисовать двумерные примеры, то нам нужно решить задачу Дирихле, я о ней уже говорил в одной из своих предыдущих статей. Для 2D это будет функция -ln r.
Теорема Ирншоу и её следствия
Итак, возвращаясь к нашему примеру с одной свободной заряженной частицей. Потенциал электростатического поля не имеет локальных минимумов, и, как следствие, потенциальная энергия одной частицы локальных минимумов не имеет. Поэтому одна частица не может находиться в состоянии устойчивого равновесия в постоянном поле. Поздравляю вас, мы только что доказали теорему Ирншоу. Но вот как быть с более сложными системами? Как применить эту теорему к ним?
Вот очередной пример, предложенный моим начальником, который должен был опровергнуть теорему Ирншоу. Давайте зафиксируем два заряда и создадим подвижное тело, состоящее из невесомой нерастяжимой палки с зарядами на обоих концах:

Интуитивно, если мы слегка сдвинем палку влево (вправо), то один из концов приблизится к фиксированным зарядам, и они его оттолкнут, вернув палку в изначальное положение. Где же подвох? Давайте нарисуем электрстатический потенциал двух фиксированных зарядов:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)
contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)
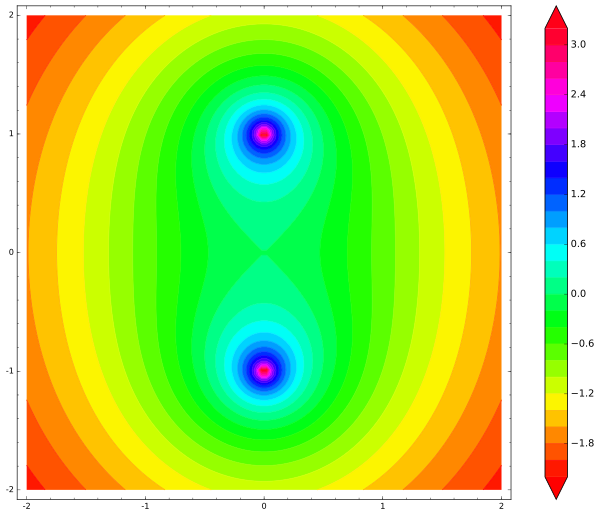
Как нарисовать потенциальную энергию нашей заряженной по концам палки? Палка имеет три степени свободы (две на перемещение и одна на вращение), поэтому график будет четырёхмерным. Давайте попробуем проигнорировать вращение и разрешим палке только параллельно перемещаться. Зафиксируем точку на палке, например, её центр, будем рисовать карту потенциальной энергии палки для положения её центра. Тогда общая потенциальная энергия палки — это сумма потенциальных энергий зарядов на конце:
var('x,y')
def unit_potential(a,b,x,y): return -ln(sqrt((x-a)^2 + (y-b)^2))
def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y)
def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y)
contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True)
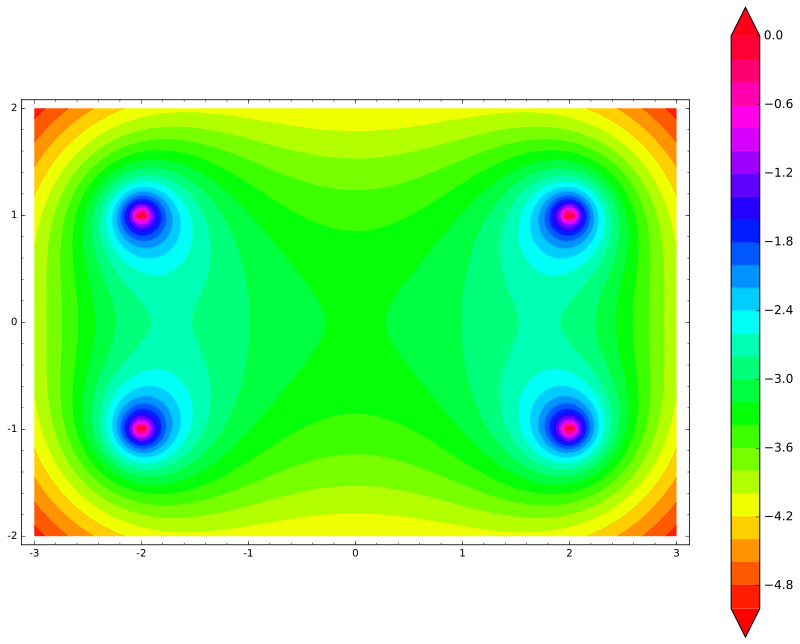
Итак, энергия палки имеет четыре пика (каждый из двух концов палки попадает на каждый из двух зарядов). Как и предполагалось, палка не захочет двигаться по горизонтали. Она убежит по вертикали!
Это логично, ведь из чего мы получили энергию? Мы сложили потенциальные энергии каждого заряда. Мы знаем, что потенциальная энергия каждого заряда — это функция с нулевым лапласианом. Их сумма тоже будет иметь нулевой лапласиан. То есть, потенциальная энергия любого (не только нашей палки!) заряженного тела не может иметь минимумов в постоянном электрическом поле!
Выводы
Ментальное изображение магнитных и электрических полей у людей, плотно не работавших с физикой, обманчиво. нас обманывает, рисуя картины минимумов энергии. К сожалению, это не так, и действительно создать мендосинский двигатель без опоры представляется затруднительным.
Какие могут быть лазейки? Теорема Ирншоу (если мы сделаем усилие и вообще применим её к магнитам) применима только системам неподвижных постоянных магнитов.
1. Мы можем попытаться создать динамическое магнитное поле
2. Диамагнетизм и всякие сверхпроводники также не входят в рамки теоремы Ирншоу
3. Подвижные вообще и вращающиеся в частности тела также не рассмотрены, наиболее известный пример левитрон
Так что, не всё ещё потеряно. Да, использование любой из этих вещей убьёт начисто лаконичность мендосинского двигателя, но магия свободно парящих в воздухе вещей перекроет всё!
Автор: haqreu