Математическая модель восприятия (Часть 2)

<< Часть 1 ^[1]

Предисловие

Последнее время ознаменовано громким триумфом промышленного внедрения искусственных нейронных сетей. Узнать ли слово или лицо, подобрать мелодию под настроение — задачи, которые с уверенностью можно считать уже решенными. СМИ пестрят то и дело появляющимися заголовками о создании искусственного интеллекта, а фантасты рассуждают о том, может ли в таких сетях самопроизвольно зародится мысль. Но действительно ли успех так грандиозен, ведь различать цифры — не значит иметь абстракцию числа, а искусно составлять предложения не означает уметь определять их смысл.
Давайте попробуем посмотреть на эти проблемы немного с другого ракурса. В природе есть один хорошо обоснованный ею процесс — эволюция: все, что не может приспособится, обычно вымирает. Именно задача приспособления на определенном этапе стала причиной развития у живых существ способности восприятия свойств внешнего мира, а необходимость оперативно отвечать на изменения этих свойств поощрило у животных развитие нервной системы. Не стоит ли поэтому попытаться представить какие именно задачи и в какой усложняющейся последовательности пришлось решать развивающемуся интеллекту животных, ведь возможно тогда, решив их, мы повторим путь эволюции и наконец приблизимся к пониманию механизмов мышления ^[2]. Вторая кажущаяся разумной идея — прежде чем приступать к конструированию машин, способных составлять представление о чем-либо (факте присутствия на картинке зеркальносимметричного фрагмента, или что у исследуемого лабиринта есть путь к выходу) попытаться:
1) назвать это «что-либо» в терминах восприятия машины;
2) охарактеризовать класс всех тех понятий, которые могут быть представлены машиной данной конструкции.
Однако назвать чем же являются такие базовые понятия как «время» и «пространство», не в рамках какой-либо формальной теории, а по своей природе — может оказаться неразрешимой проблемой. Здесь спасает то, что во многих случаях процесс восприятия можно формально заменить (мульти) символьной последовательностью, изображающей состояния рецепторов через одинаковые достаточно малые промежутки времени. После такой подмены оказывается уже не важной истинная природа понятий, подлежащих восприятию — важно лишь то, чем они являются в терминах упомянутой символьной последовательности. С этой новой позиции интересно рассмотреть такие понятия, как «время», «место», «число», «память», «будущее». В настоящей части моей работы я попытался найти подход к определению понятия симметрии и понятия формы, а так же показать как фактически они реализуются на учебном примере «зрительного зонда». Если Вы не читали первую часть статьи ^[1], рекомендую Вам это сделать, поскольку части не независимы и дальнейшее содержание может оказаться непонятным

Внутреннее определение симметрий

Математика знает много примеров, когда те или иные свойства не могут быть установлены «изнутри». Пожалуй, самый известный из них– это утверждение о невозможности лишь средствами арифметики установить её непротиворечивость. Другой же говорит о том, что ни на одном языке нельзя так охарактеризовать, какие из его фраз являются истинами, чтобы ничего не упустить и не прийти при этом к противоречию. Вообще, самоопределимость и самоописуемость – частые причины возникновения различных парадоксов и антимоний. Интересно, а что может «сказать» о себе зонд? Имеется в виду, о каких качествах и свойствах зонда может составить представление человек лишь на основании опыта наблюдения за его индикаторами. К примеру, взглянув хотя бы раз на зонд, как на предмет, трудно не заметить его симметричность. А может ли ее «заметить» сам зонд, ведь никакого способа «видеть себя» у него нет? Достаточно неожиданным оказывает, что обо всех симметриях зонда удается составить представление исключительно по закономерностям изменения цвета клеток, воспринимаемых его рецепторами. Методу, которым это может быть сделано, посвящено ближайшее повествование.
Для начала найдем каждому участвующему в дальнейшем описании зонда понятию его «индикаторного двойника». Способы раскраски семи клеток, обозреваемых зондом, назовем цветовые конфигурации. Поскольку над одними и теми же клетками зонд может оказаться в разных положениях (скажем, если среди его простых движений имеются повороты), то, если быть более точными, под цветовой конфигурацией будем понимать исчерпывающее описание того, над клеткой какого цвета находится каждый его цветочувствительный рецептор. Различные цветовые конфигурации приведены на рис.15

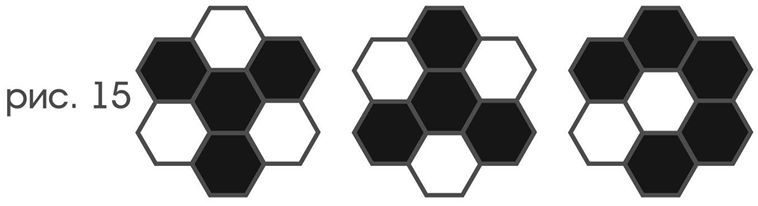
Двойственным понятию цветовой конфигурации является понимание цветовой конфигурации в несобственном смысле – исчерпывающее описание того, какие цветовые индикаторы зонда горят, а какие нет.
Так как по условию простое движение происходит в точности тогда, когда гаснет представляющий его цветовой индикатор, то эти явления оказываются двойственными друг другу, причем последнее разумно назвать простым движением в несобственном смысле. Серию следующих друг за другом простых движений назовем общим или составным движением. Всякое простое движение, как серия длины 1, является при таком определении в том числе и общим. Двойственным к общему движению будет явление, состоящее в том, что сначала гаснет только лампа ∆_1, затем только лампа ∆_2, …, затем только лампа ∆_n и между этими моментами не гаснет ни один индикатор движения.
Это явление Σ, изображаемое как ∆_1*∆_2*…*∆_n, в силу определения простого движения в несобственном смысле оказывается общим движением в несобственном смысле.
Легко видеть, что если Σ_1,Σ_2,… Σ_k – общие движения (в собственном или несобственном смысле), то общим движением будет и явление Σ_1*Σ_2*… *Σ_k, когда сначала происходит Σ_1, затем Σ_2,…, затем Σ_k, и между двумя из этих идущих друг за другом движений никаких движений не происходит.
Некоторые сложные движения (в собственном смысле) на самом деле по своему завершению оставляют зонд в прежнем месте в прежнем положении. Поэтому их стоило бы назвать стационарными. Таковыми, например, являются ↑*↓, &nwarr;*&nearr;*↓ и ↷*↶. А можно ли определить свойство двойственное стационарности по отношению к общим движениям в несобственном смысле. Непосредственный перевод формулировки этого свойства потребовал бы предварительного определения в терминах индикаторов понятий «место на гексагональной решетке» и «положение зонда», которыми мы пока не располагаем. Попробуем найти косвенный путь. Заметим сначала, что всякий раз цветовая конфигурация, наблюдаемая перед выполнением любого стационарного движения точно такая же, что и по его завершению. В этом смысле все стационарные движения «сохраняют» цветовые конфигурации. На самом деле, если гексагональная решетка раскрашена достаточно разнообразно, других движений, сохраняющих цветовые конфигурации нет. Эти два обстоятельства говорят о равнозначности свойств «стационарность» и «движению сохранять цветовые конфигурации», последнее из которых легко переводимо на язык индикаторов: нужно лишь термины «движение» и «цветовая конфигурация» воспринимать в несобственном смысле. Упомянутая же равнозначность дает нам право этот перевод считать свойством, двойственным свойству стационарности. Для выражения свойства стационарности движения Σ (в собственном или несобственном смысле), будем использовать формальную запись Σ ≃E.
Движения U и V такие, что их последовательное выполнение в любом порядке является стационарным движением (U*V≃E и V*U≃E), разумно назвать взаимнообратными. Таковы, к примеру, пары ↑и↓, и, ↷и ↶, (&nwarr;*&nearr;) и↓ среди собственных движений, а так же n[↑] и n[↓], n[&nwarr;] и n[&searr;], n[↷] и n[↶], (n[&nwarr;]*n[&nearr;]) и n[↓] — среди несобственных.
Можно ли распространить применение знака эквивалентности “≃” на нестационарные движения? Так, общее движение ↑ и (&nwarr;*&nearr;), будучи различными по способу выполнения, по сути, приводят к одному и тому же результату. Вообще, если две инструкции по результату их выполнения, дают одно и то же перемещение зонда, то этот факт может быть всегда установлен уже по виду этих инструкций. Например, где бы ни находился зонд, выполнение либо: “сместить ↑, сместить, затем ↷ », либо: “сместить &nwarr;, затем ↷, сместить ↑» изменят его место и положение одинаковым образом. «Эквивалентность» движений двух типов может быть подмечена также путем непосредственного наблюдения за их выполнением зондом на гексагональной решетке: достаточно как-нибудь однообразно в обоих случаях описать конечное положение через начальное, (скажем, «всякий раз по завершении движения U зонд оказывается смещенным на семь клеток в направлении «4», одну клетку в направлении «6» и повернутых на 60° против часовой стрелки, отсчитывая от его положения на момент начала выполнения этого движения»). Если описания получились одинаковыми, то типы «эквивалентны». Тем не менее, никакого простого способа установить «эквивалентность» движений по наблюдению лишь за индикаторами зонда, по всей видимости, нет. Здесь ситуация отдаленно напоминает следующую: пусть имеется много двухдверных шкафов, за каждой дверью которых прячется по цветку ромашки или тюльпана, причем цветы внутри одного шкафа всегда одинаковые: либо оба — ромашки, либо тюльпаны (рисунок 16).

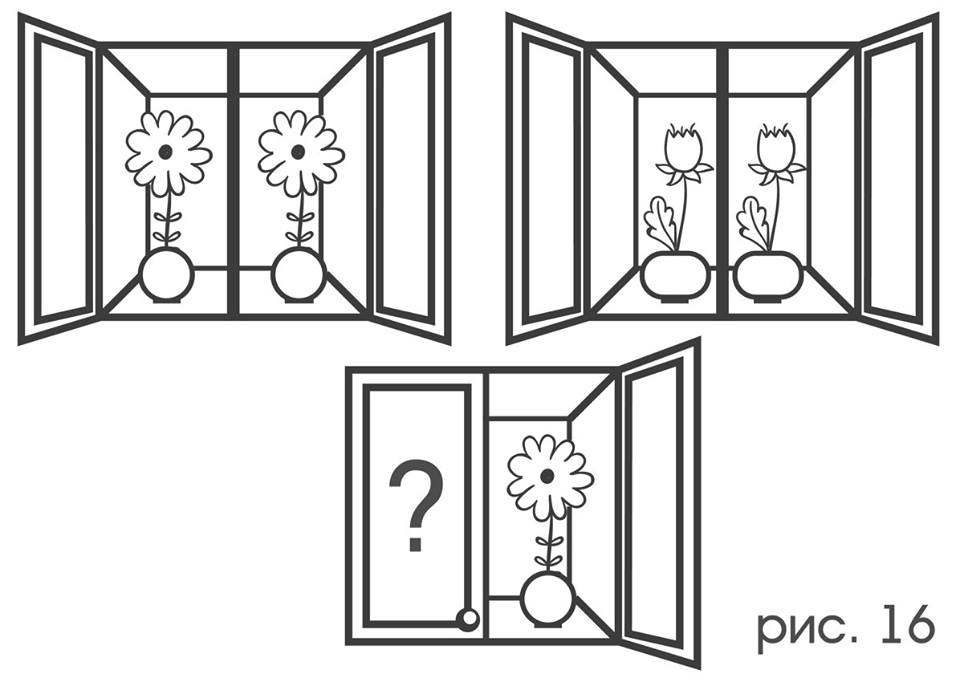
Но можно ли догадаться до этой закономерности, если в каждом шкафу можно открывать только одну дверцу? Наблюдая за индикаторами трудно понять, что какие-нибудь два движения (в несобственном смысле) приводили бы всегда к одинаковым изменениям цветовых конфигураций. Ведь на деле каждый раз оказывается выполненным только одно из этих движений. Невозможность простого определения «эквивалентности» делает несколько затруднительным применение обычных алгебраических методов при построении «теории зонда» и заставляет пользоваться сильно урезанным аналогом эквивалентности – стационарностью. Однако несколько полезных правил алгебраического характера выразить все же удается:
i) Пусть U и V – стационарные движения, тогда стационарными будут и движения U*V и V*U;
ii) Пусть U*V — стационарные движения, тогда каково бы ни было стационарное движение Σ, движение U*Σ*V также стационарно.

Доказательство приведенных выше правил, когда все термины понимаются в собственном смысле, следует из определения стационарности — свойства движений в итоге не менять положение зонда, а из-за принципа двойственности эти правила оказываются верны и в несобственном случае. Точно также, доказав какое-нибудь утверждение о проективной плоскости, вы можете в силу принципа двойственности проективной геометрии считать доказанным и утверждение, получающееся из доказанного заменой слов “точка” на “прямая” и “ прямая” на “точка”. Пример еще одного важного для описания зонда свойства, обобщающего свойство взаимной обратимости, демонстрирует тройка движений — &nwarr;,&nearr;, ↓. Условимся говорить, что движения U,V и W образуют циклическую тройку, если их выполнение в любом порядке приводит к стационарному движению. Несложный анализ показывает, что среди элементарных смещений есть в точности две циклические тройки: (&nwarr;,&nearr;, ↓) и (&swarr;,&searr;,↑), получающиеся друг из друга заменой входящих в них движений на обратные к ним. Уже было показано, как, наблюдая за индикаторами, выделить среди них шесть лампочек, представляющих элементарные смещения, но не дано никакого фактического способа указать, которая из этих лампочек представляет, скажем, смещение ↑, а которая. Забегая вперед, предупредим читателя, что такого способа, в силу симметричности зонда и произвольности его соединения с циферблатом, попросту нет, однако двойственный характер свойств цикличности и взаимной обратимости дает возможность в упомянутой шестерке ламп указать пары, соответствующие парам взаимнообратных движений, и тройки, соответствующие циклическим тройкам. Для простоты будем говорить о взаимнообратных индикаторах и их циклических тройках. Оказывается, что этих двух свойств вполне достаточно, чтобы выразить в двойственных терминах понятие симметричности зонда, как предмета. Зонд как предмет можно “накладывать на себя”, переворачивая его подобно монетке, или поворачивать вокруг центрального рецептора. Любое такое “наложение” определяет перестановку между отметками “12”, “2”, “4”,… ,”10”, связанного с ним циферблата. Например, при повороте на 60 градусов по ходу часовой стрелки «12» накладывается на «2», «2» — на «4», …, «10» — на «12». Эта перестановка в виду принятого соответствия между отметками циферблата и элементарными смещениями порождает перестановку: "↑"→"&nearr;"→"&searr;"→"↓"→"&swarr;"→"&nwarr;"→"↑". Последняя, как можно увидеть на рис.17, сохраняет свойства цикличности и взаимной обратимости в том смысле, что если два смещения взаимнообратны, то они переводятся во взаимнообратные, а если некоторые три из них образуют циклическую тройку, то и их образы также образуют циклическую тройку.

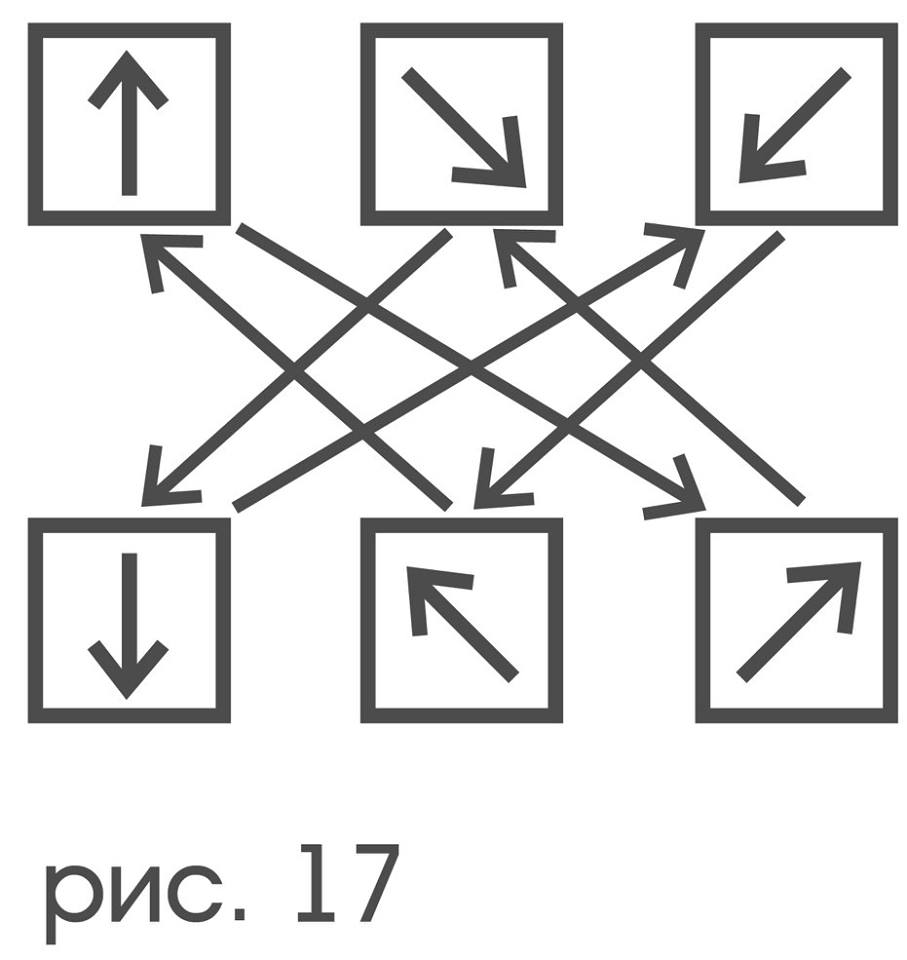
На самом деле, описанная ситуация с сохранением цикличности и взаимной обратимости не случайна: цифры, соответствующие взаимнообратным движениям диаметрально противоположны на цифербалате, соответствующие же циклическим тройкам – расположены по концам правильных трехконечных «звезд» (рис. 18), а всякое наложение зонда на себя безусловно сохраняет диаметральную противоположность его точек и форму «звезд».

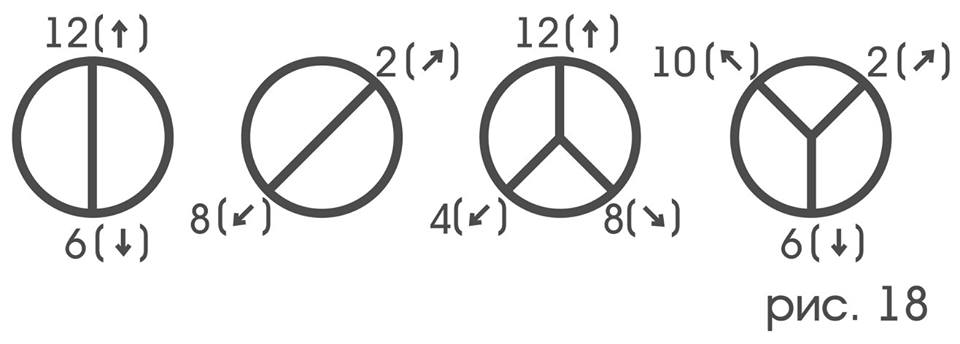
Путем несложных рассуждений можно показать, что и обратно: всякая перестановка среди элементарных смещений, сохраняющая свойство взаимной обратимости и цикличности порождается в точности одним наложением зонда на себя.
Совокупность всех таких перестановок назовем группой внутренних симметрий зонда. Это название оправдывается следующим фактом. Присвоим какие-нибудь имена всем индикаторам цвета (обозначим множество задействованных при этом имен через К) и всем индикаторам, представляющим элементарные смещения (соответствующее множество обозначим через М). Достаточно подробным описанием зонда (как системы закономерностей состояний индикаторов) будет список L всех таких троек имен x, y, p, для которых индикатор цвета x лежит по направлению элементарного смещения, представляемого индикатором p от индикатора цвета y (в несобственном смысле). Пусть m – перестановка имен индикаторов цвета на М, а k – перестановка имен индикаторов, представляющих элементарные смещения на К. Что если выполнить эти перестановки одновременно внутри списка L? Вообще говоря, как вид списка, так и смысл, который в нем заключается, после этого могут измениться. Однако если k и m порождены некоторым наложением зонда на себя, то единственным результатом обоюдного выполнения этих перестановок в списке станет изменение в нем порядка перечисления троек, никак не влияющее на его смысл.
Пусть теперь некоторые m и k после своего выполнения над списком L меняют в нем разве что только порядок следования троек, оказывается, верно и обратное: они должны быть порождены некоторым наложением зонда на себя (как предмета), а все такие m образуют группу изоморфную группе внутренних симметрий зонда. Более подробно о связи симметрий объекта с симметриями его описаний речь пойдет в следующей главе.

Механизмы восприятия формы

Как определить понятие формы? Давайте представим, как постигают его дети. Возьмем, например, развивающую игру для самых маленьких — деревянный пазл – это набор из предметов разных геометрических форм и доски с подходящими под формы предметов отверстиями. Ребенок решает непростую для себя задачу: какой формы должен быть предмет, чтобы его можно было вставить в отверстие. Первая удача в этой игре ждет его с элементом круглой формы – он симметричен относительно поворотов и легко узнаваем. А вот с элементом пазла в форме флажка, случайно его перевернув, ребенку придется изрядно повозиться.

Наблюдая за птицами, в особенности за воронами и попугаями, легко заметить, как рассматривая предметы, они наклоняют голову то вправо, то влево. Известно, что многие живые существа (в том числе более простые, чем вороны) способны узнавать предметы в их зеркальном отражении, тогда как увидеть отраженный предмет в его эталонном положении можно лишь, поменяв глаза местами и перевернув в них сетчатку.
Понятие формы вещей не относится только к зрительному восприятию: люди легко узнают любимые мелодии, даже если сыграть эти мелодии немного не так, как в оригинале: на октаву выше или ниже, в замедленном темпе или в ускоренном; даже, если мелодия будет насвистана, её по-прежнему можно узнать. Не является ли музыка поэтому формой последовательности звуков?
Оказывается, что часто о форме или симметрии вещи удается судить лишь по ее описанию. Этот метод предпочтителен тем, что не требует каких-либо манипуляций с самой вещью и, быть может, именно он позволяет узнавать мелодии, не имея возможности замедлять или ускорять время или же менять октаву звучания, а форму предметов – не наклоняя голову и не проталкивая их через отверстия.
Сами вещи, как реальные, так и математические абстракции, в большинстве случаев являются совокупностями более простых вещей, находящихся друг с другом в определённых отношениях: кирпичная стена – совокупность расположенным определенным образом друг относительно друга кирпичей, рабочий коллектив – совокупность людей, связанных между собой отношениями подчиненности.
В качестве еще одного примера будем рассматривать произвольный треугольник, как совокупность трех отрезков с отношениями «иметь длину» и «иметь общий конец».

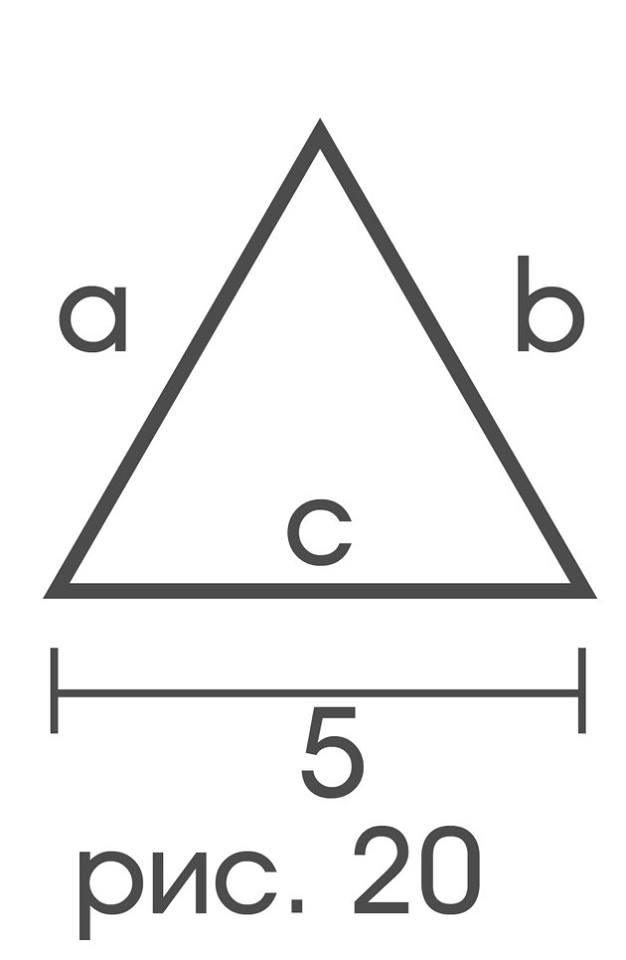
В этих терминах равносторонний треугольник на рис.20 допускает следующее исчерпывающее описание:
«Треугольник ∆ — совокупность трех отрезков a,b,c, причем:
1) один из концов a — общий с b, другой — с c, длина a равна 5;
2) один из концов b- общий с c, другой — с a, длина b равна 5;
3) один из концов c — общий с a, другой — с b, длина c равна 5
».
Сложно не заметить удивительную симметричность этого описания, до некоторой степени отражающего в себе тем самым все симметрии определяемого им треугольника. Чтобы придать сказанному большую ясность, наложим треугольник на себя, повернув на 120 градусов (рис.21).

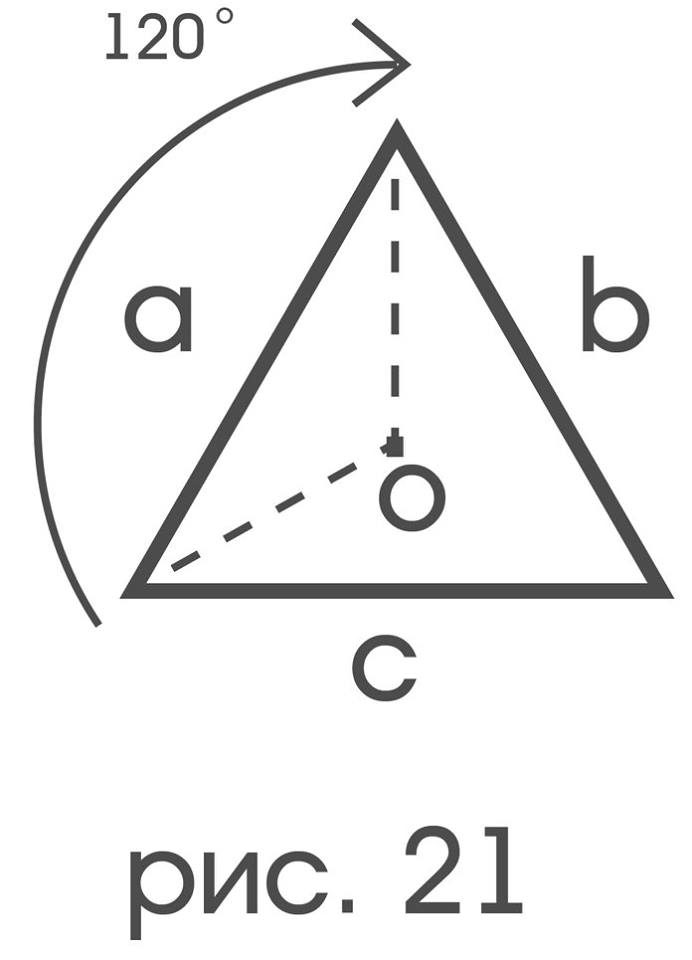
По завершению этого движения a перейдет «на место» b, b — «на место» c, c в свою очередь — «на место» a. Если формально осуществить выписанную перестановку в описании ∆, то получится следующее:
«Треугольник ∆ — совокупность трех отрезков a,b,c, причем:
1) один из концов b- общий с c, другой — с a, длина b равна 5;
2) один из концов c — общий с a, другой — с b, длина c равна 5
3) один из концов a — общий с b, другой — с c, длина a равна 5
».
Отсюда видно, что в результате такой подстановки описание ∆, за исключением несущественного изменения порядка перечисления, полностью сохраняет свой вид. Как может догадаться читатель, верно и обратное: всякая перестановка среди a,b,c, сохраняющая с упомянутой оговоркой вид описания ∆, порождается некоторой его геометрической симметрией.
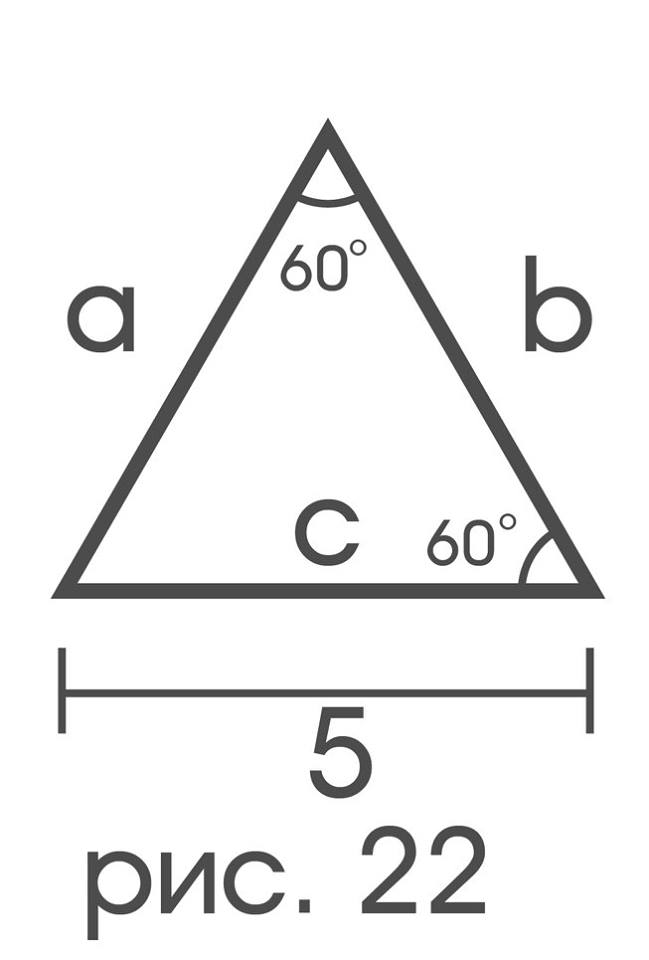
Подобная двойственность между симметриями вещи и симметриями ее описания возникает не всегда. Конечно, если описание уже обладает какой-либо симметрией (существует перестановка имен вещей, фигурирующих внутри описания, не меняющая его вид ), то она обязательно порождается симметрией вещи. Обратное, однако, не верно: тому же одностороннему треугольнику можно дать описание, не обладающее никакими симметриями, кроме тождественной:
«Треугольник ∆ — совокупность трех отрезков a,b,c, причем:
1) один из концов a — общий с b, другой — с c;
2) один из концов b- общий с c, другой — с a;
3) один из концов c — общий с a, другой — с b;
4) длина a равна 5;
5) угол между a и b равен 60°;
6) угол между b и c равен 60°».

Уделим внимание теперь случаю, когда вещью является граф. Всякий граф можно считать совокупностью вершин с двуместным отношением «… соединен ребром с …», а, чтобы получить исчерпывающее описание конкретного графа, достаточно просто перечислить все пары его вершин, находящихся в этом отношении. Такое описание условимся называть списком инцидентностей. Для наглядности вершины графа можно представить себе пуговицами, а ребра, соединяющие их, — нитями.
Всякое наложение (отображение множества вершин графа на себя), при котором на каждую вершину в итоге накладывается ровно одна вершина и на каждое ребро – в точности одно ребро, естественно назвать симметрией этого графа, если же наложение с перечисленными условиями возможно между двумя различными графами, то естественно говорить об изоморфизме между графами одинаковой формы.
Пусть для читателя будем несложным упражнением показать, что всякая симметрия графа соответствует (дуальна) некоторой симметрии списка его инцидентностей, а два графа имеют одинаковую форму тогда и только тогда, когда список инцидентностей одного можно получить из списка инцидентностей другого простой заменой (точной подстановкой) имен вершин в этом списке.
На рис.23 изображены три по-разному раскрашенных экземпляра одного и того же графа.

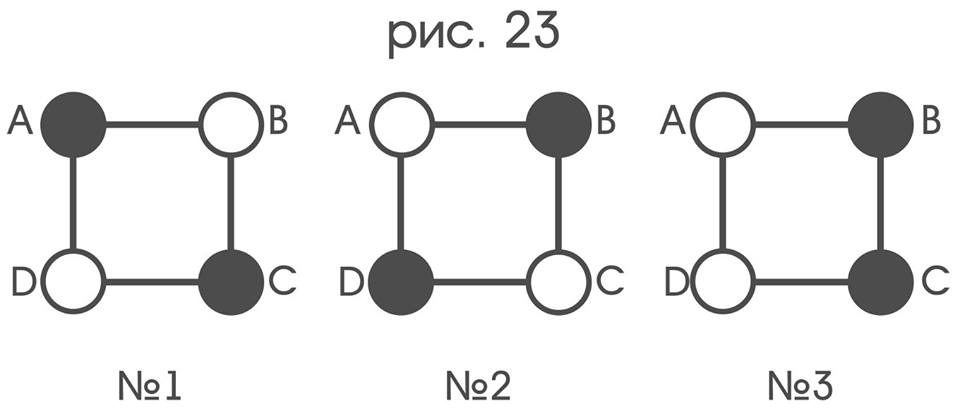
Наверное, самый непосредственный способ получить описание экземпляра графа с выбранной раскраской – присоединить к списку его инцидентностей перечисление того, какой цвет имеет каждая его вершина. Совершенно очевидно, что не все симметрии, ровно как и не все изоморфизмы графов, оставляют выбранную раскраску неизменной: так как при попытке наложить экземпляр №1 на себя поворотом на 90° наложение каждой вершины будет выполнено на вершину противоположного цвета. Разумно поэтому симметрии раскрашенного графа, при которых накладываются друг на друга только вершины одинакового цвета, назвать симметриями выбранной раскраски, а если же между двумя графами возможен изоморфизм с описанным свойством, то говорить об изоморфизме между раскрасками двух графов одинаковой формы (или об одинаковой с точностью до этого изоморфизма форме раскраски). Согласно данным определениям, раскраски экземпляров №1 и №2 имеют одинаковую форму, отличную от формы раскраски экземпляра №3.
Но что делать, если никакого физического способа накладывать одни графы на другие нет? Как тогда определить форму раскраски? Пусть снова для читателя окажется несложным упражнением показать, что всякая симметрия выбранной раскраски графа соответствует (дуальна) такой перестановке имен его вершин, которая сохраняет как список инцидентностей, так и список перечисления цветов вершин. Раскраски же двух различных графов имеют одинаковую форму тогда и только тогда, когда оба упомянутых списка для одного из них можно получить из списков для другого простой подменой (точной подстановкой) имен их вершин.

Теперь настало время пролить немного света на то, как происходит сличение формы предметов. Удобней всего это сделать на примере уже знакомого нам зонда, причем рассмотрение коснется крайнего случая стесненности его простых движений, когда последние ограничены исключительно элементарными смещениями. Оказывается, что уже их вполне достаточно, чтобы по отношению к цветовым конфигурациям ячеек решетки на рис.24 сказать, что флажки a) и б)

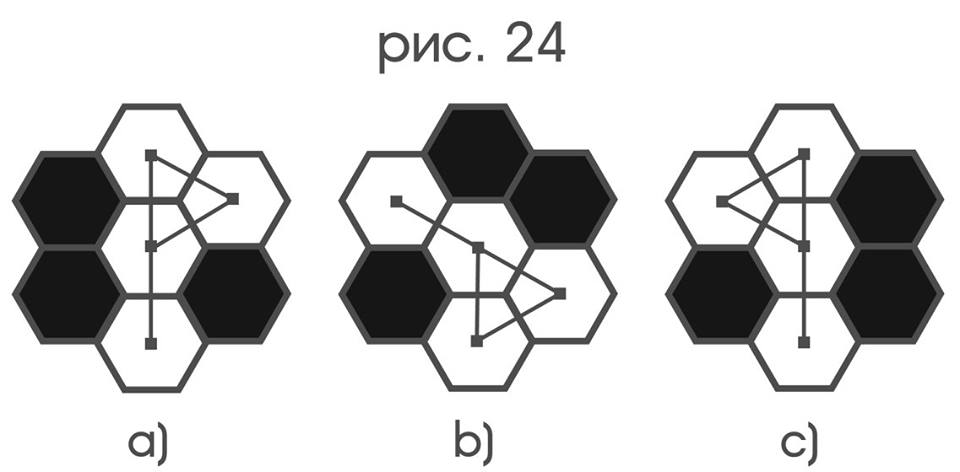
одной формы с точностью до «поворота», флажки б) и с) одной форм с точностью до «зеркального отражения», тогда как сам зонд, еще раз подчеркну, лишен какой-либо возможности поворачиваться или «зеркально отражаться». В описанной ситуации понятия «поворот» и «зеркальное отражение» получат корректные определения чисто языковыми методами. Во многом все перечисленное возможно благодаря тому замечательному факту, что, как и область решетки в «поле зрения зонда», так и сам зонд имеют ровно такой же набор симметрий, каким обладает «зонтичный» граф рис 25.

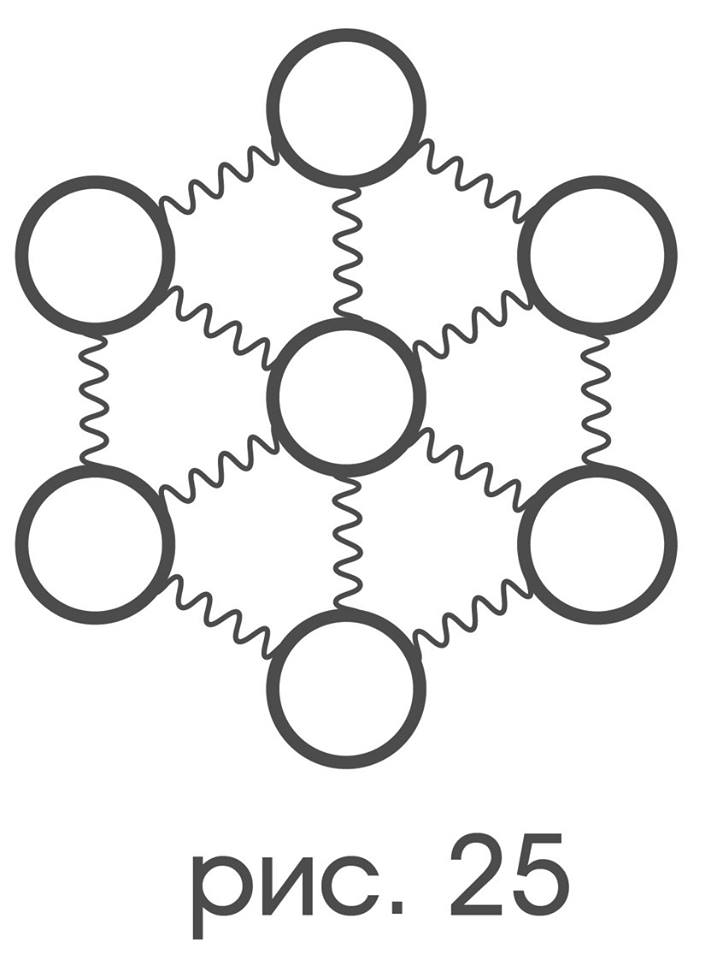
Чтобы дать обещанный способ сличения форм цветовых пятен, будет показано, каким образом на множестве ячеек под зондом, множестве цветочувительных рецепторов и множестве связанных рецепторами индикаторов ввести структуру, превращающую каждое из этих множеств в зонтичный граф. Тем самым задача сличения форм цветовых пятен окажется эквивалентной задаче сличения форм раскрасок зонтичного графа.
Идея решения последней без вовлечения в порочный круг использования еще не определенных геометрических понятий заключается в том, чтобы о симметриях зонтичного графа судить по симметриям его описания. Но тут-то и возникает проблема: какие из этих симметрий стоит назвать отражениями, а какие поворотами (других симметрий у зонтичного графа нет), ведь без осуществления непосредственных манипуляций над вещью теряется смысл слов «отражение» и «поворот», в то время как описание при выполнении перестановок имен в нем вовсе не поворачивается и не отражается?
Один из способов вернуть потерянный смысл – найти категоричное свойство перестановок, соответствующих каждому конкретному типу симметрий. Подходящим для этих целей и испытанным свойством оказывается структура орбит. Так симметрии, в интуитивном понимании являющейся поворотом на 60°, соответствует перестановка

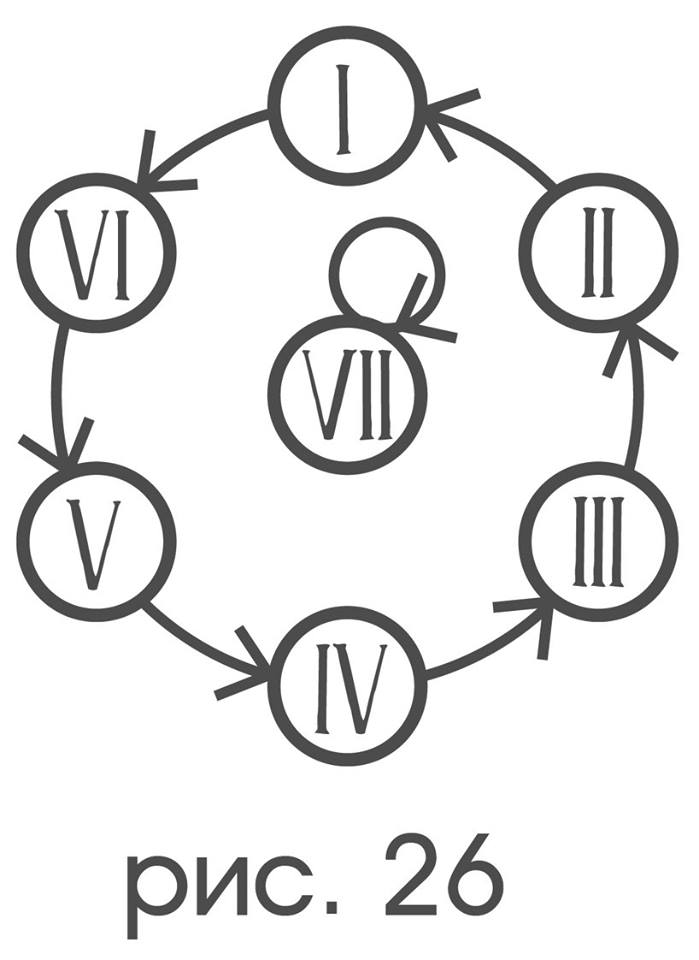
и только повороты на 60° имеют структуру орбит π:

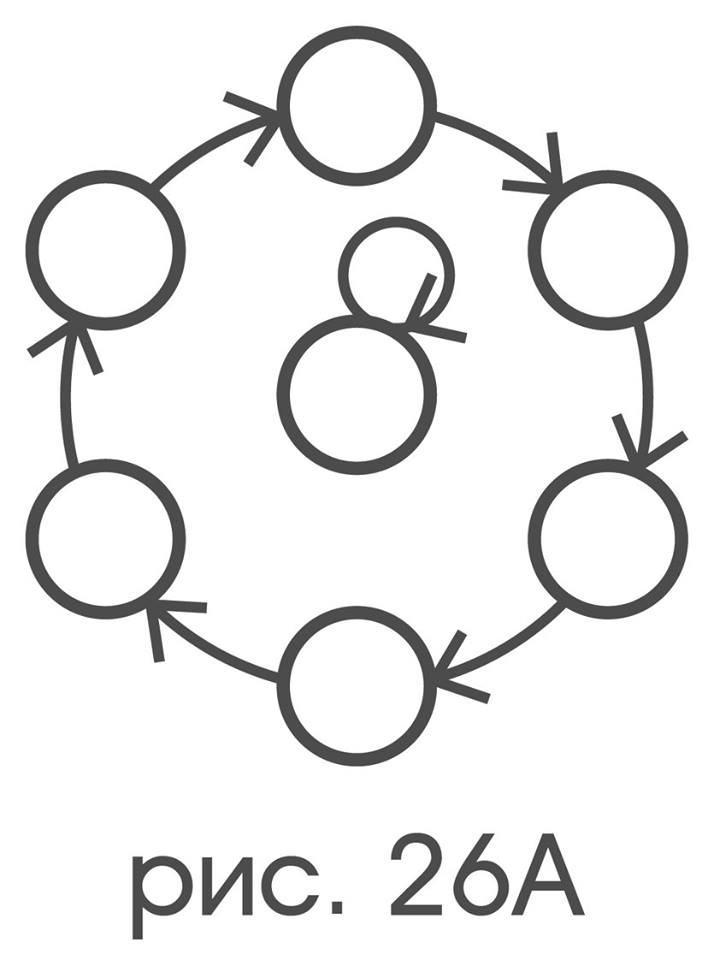
Симметрии, в интуитивном понимании являющейся зеркальными отражениями, и только они имеют структуру I:

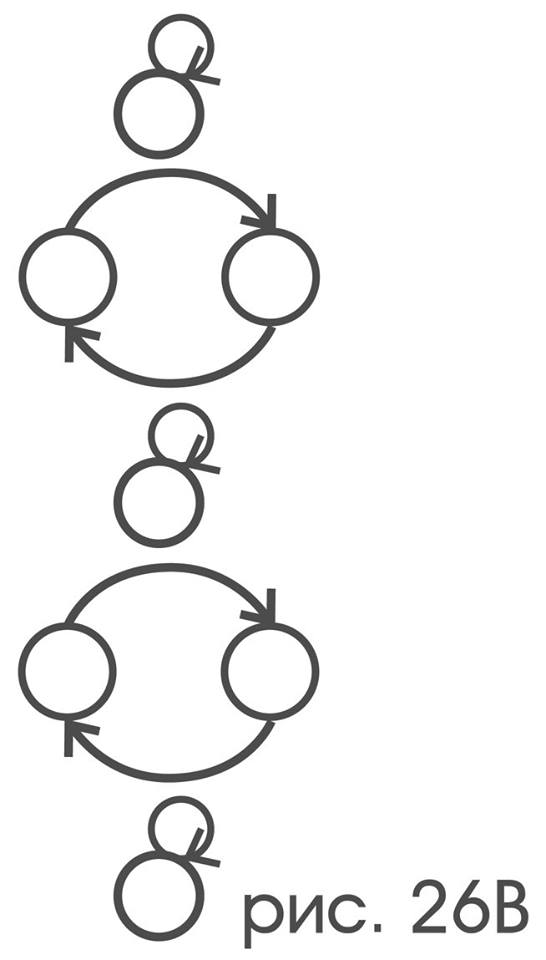
Структуру орбит E:

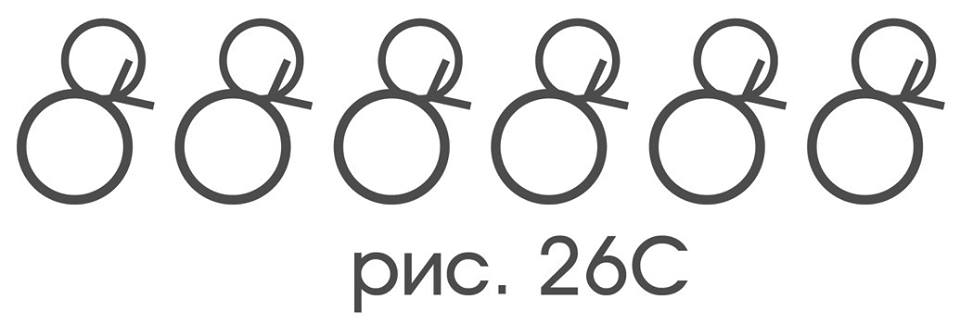
имеет лишь тождественная симметрия,
структуру

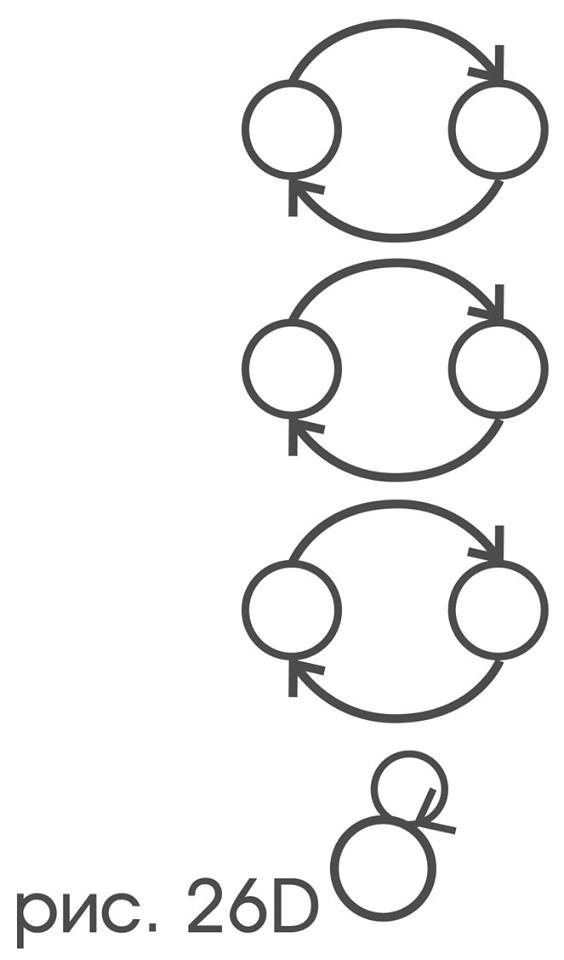
— только поворот на 180°,
и только «поворот на 120°» однозначно соответствует структуре:

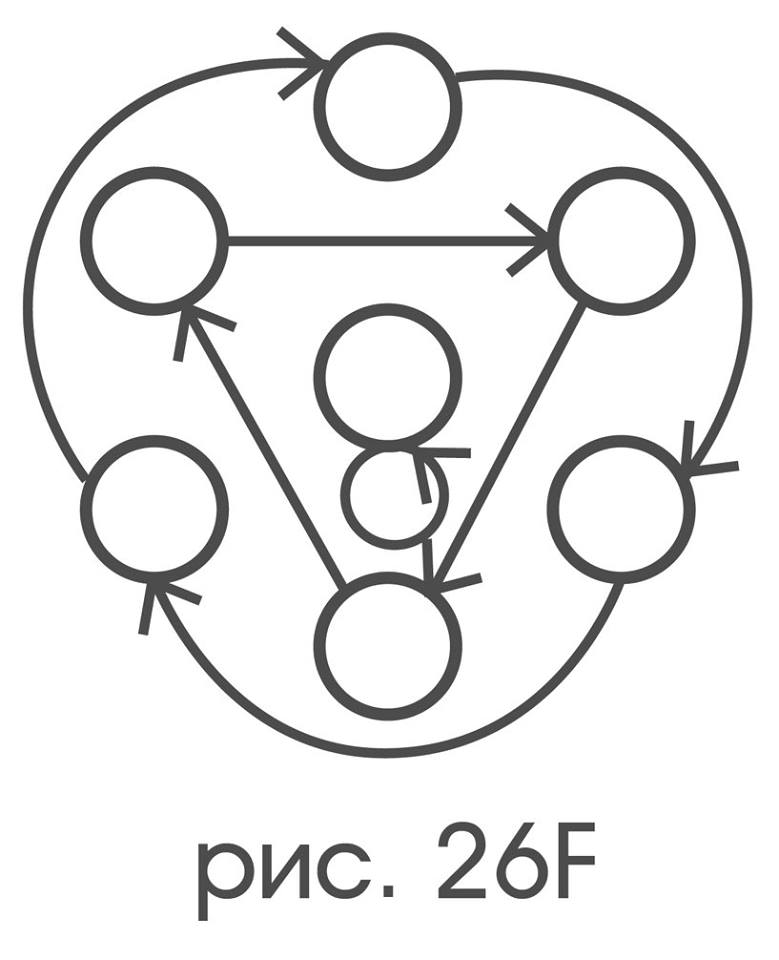
Этим завершается перечисление всех возможных типов симметрий зонтичного графа.

Давайте превратим область решетки, являющуюся «полем зрения» зонда в граф, вершины которого — суть клетки этой области, а ребра между ними изображают отношение «быть смежным по стороне» (рис 27).

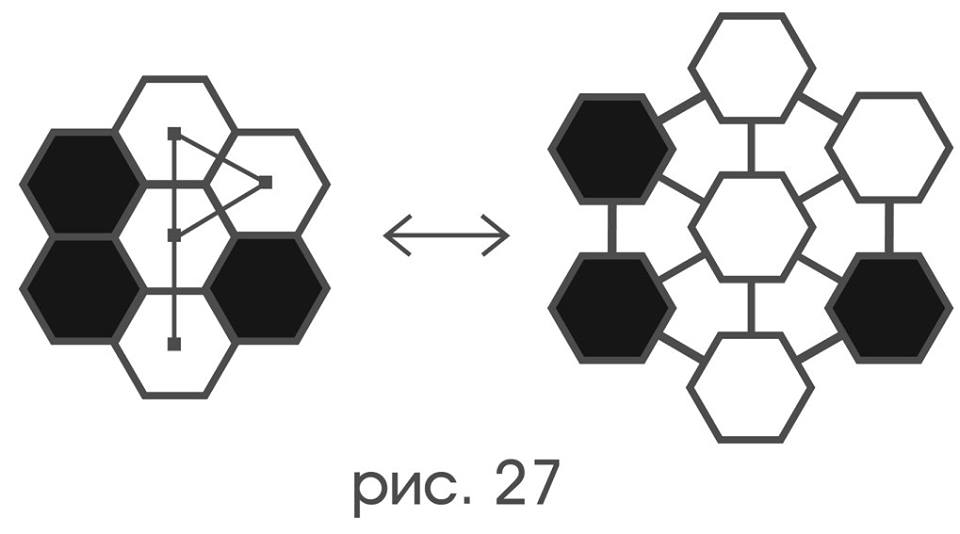
Такой метаморфоз позволяет сравнивать обозреваемые зондом картинки, как раскраски получившегося графа, путем анализа их описаний, не требуя при этом никакой «физической» возможности что-либо друг на друга накладывать. Например, цветовым конфигурациям рис.24 соответствуют раскраски a’), b’), c’) зонтичного графа (рис 28), причем, если под “поворотом”

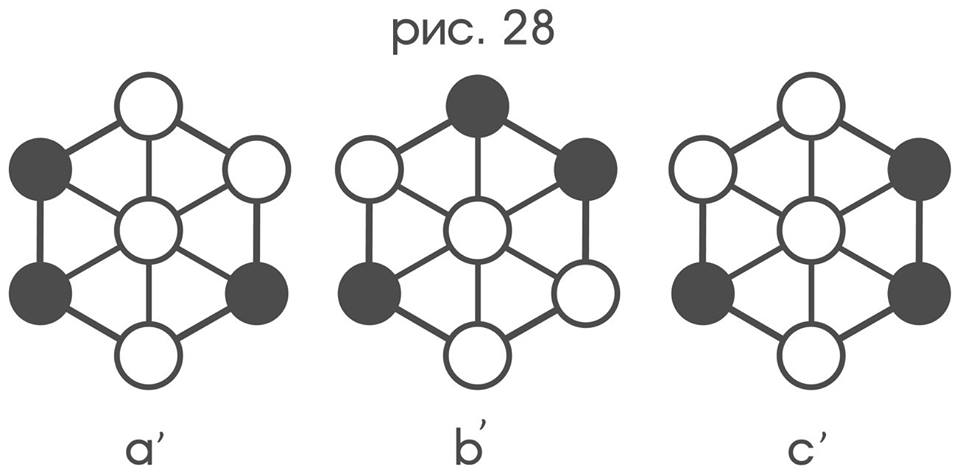
и “зеркальным отражением” понимать наличие у орбит перестановок, отвечающих изоморфизмам раскрасок той или иной структуры, то a’) и b’) действительно имеют одинаковую форму с точностью до поворота на 120°, а b’) и c’) — с точностью до зеркального отражения.
Читатель наверное обратил внимание на то, что с самого начала зонд изображался в виде зонтичного графа с рецепторами-вершинами и жесткими стержнями-ребрами. Можно было бы поэтому сказать, что сравнение формы цветовых конфигураций на его рецепторах снова сводится к анализу описаний раскрасок упомянутого графа, однако жесткие стержни невозможно увидеть с помощью рецепторов или составить о них представление из наблюдений за индикаторами. Тем не менее, все же существует способ превратить множество рецепторов в доступный для восприятия зонтичный граф с той же самой структурой: для этого нужно лишь заметить, что рецептор x «соединен стержнем» с рецептором y в точности тогда, когда выполняется отношение:
“существует такое элементарное смещение S, что x лежит по направлению S от y”. Именно в этом месте важным является присутствие среди простых движений зонда всех его элементарных смещений, поскольку тогда справедливость или несправедливость последнего отношениями между конкретными рецепторами x и y может быть установлена путем достаточно долгого наблюдения за воспринимаемыми ими цветами. Ещё одно замечание состоит в том, что элементарных смещений среди простых движений оказывается достаточным, чтобы судить об одинаковости формы и двух конфигураций, получаемых друг из друга поворотом или зеркальным отражением, даже когда сам зонд в принципе не может быть повернут или зеркально отражен.
Осталось заметить, что фраза “∃ S (S есть элементарное смещение) ∧(x лежит по направлению S от y) ” допускает непосредственный перевод в двойственные термины, тем самым определяя двойственное отношение на множестве индикаторов цвета, превращающее это множество в зонтичный граф. Последнее означает, что лишь по наблюдению за букетами ламп, связанных с зондом, даже когда все его простые движения сводятся к плоскопараллельным смещениям и сам зонд непосредственному наблюдению недоступен, удается все же адекватно и исключительно во внутренних терминах определить понятия «поворот», «зеркальное отражение» и способ сличения формы цветовых конфигураций индикаторов.

Автор: Sergey_Kovalenko

Источник ^[3]