12 мая мы с товарищами зашли в московское метро с его открытием утром и, не выбираясь наверх, посетили все 199 доступных в данный момент станций до закрытия метрополитена. Зачем мы всё это сделали – совершенно не ясно, но я попробую рассказать, как так получилось.
Давным-давно, кажется, с год назад жена сказала мне, что хотела бы как-нибудь сфотографировать все станции метро в Москве. Я тогда пошутил, что под такое дело можно рассчитать оптимальный маршрут, позволяющий посетить все станции, напрягаясь по-минимуму. Пошутил и забыл, а тут зимой вспомнил и решил попробовать.
По мере изучения вопроса я обнаружил, что идея сама по себе не то чтобы очень нова – в нью-йоркской подземке аналогичные соревнования проходят с 1966 года. Что же касается московского метро, то ЖЖ-пользователь estrella-de-sur полгода назад проехал его за 12 часов 36 минут (расчётное время – 11 часов 50 минут) по правилу «один шаг на каждую станцию». Но у нас была другая задача – мы хотели выйти на каждой станции и по возможности красиво её сфотографировать. Это означало, что нам в большинстве случаев придётся ждать на ней следующего поезда. Исходя из этого я и строил расчёт.
Предупреждение: если вы умеете решать задачу коммивояжёра на 200 узлах (с помощью генетических алгоритмов или без них) – вас, скорее всего, ждут в другом месте. Можете просто пролистать пост и посмотреть картинки.
Где взять данные
Первым делом для такой задачи нужно было оцифровать граф метро (узлы – станции, рёбра – переезды и переходы) и дополнить его элементы разной полезной информацией: для станций – географические координаты, время открытия-закрытия и интервалы следования поездов в разное время суток; для рёбер – время перегона или перехода между станциями.
Станций в Москве много (Саларьево на тот момент ещё не открыли, но всё равно хватало), и руками всё это делать не хотелось совершенно. Тогда я обратился к сайту Яндекс.Метро. Для старта это было в самый раз, но этот сервис использует усредненные оценки времени, а для серьезного расчёта нужно было иметь более точные сведения. Тут я вспомнил пару довольно древних программ с народными замерами времени – pMetro и mMetro – это, если кто не знает, такие десктопные калькуляторы метромаршрутов. Первая почти перестала официально обновляться в 2011 году, вторая – ещё раньше, но всё лучше, чем ничего.
Среди файлов в папке pMetro обнаружился Moscow.pmz, на деле оказавшийся обычным zip-архивом с кучей файликов в архаичном .ini-формате. Там нашлась почти вся нужная информация (на схеме не хватало нескольких самых свежих станций). Я наваял одноразовый парсер всего этого в tsv и довбил руками отсутствующие станции и перегоны, «прозвонив» тайминги для них на Яндекс.Метро. Координаты новых станций я взял из статей Википедии.
Схема в итоге получилась вот такой (проекция, конечно, не Меркатора, но суть передаёт):
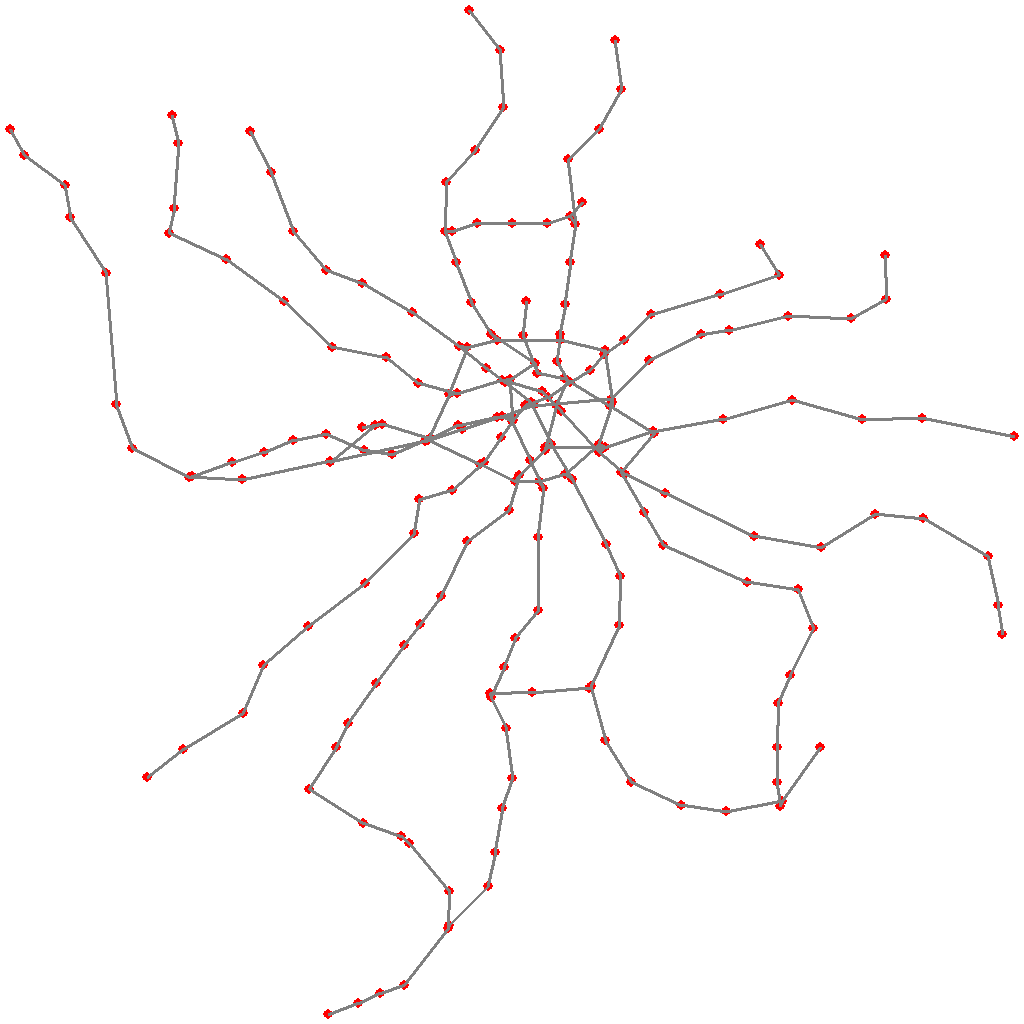
(тут я нарисовал ещё и линию монорельса, но, в дальнейшем, было решено от неё отказаться)
Теперь предстояло попробовать со всем этим взлететь.
Геном коммивояжёра
Итак, нужно было решить классическую задачу коммивояжёра в постановке на неполном графе над 200 вершинами. Опыт предков учит нас, что задача эта NP-полна и даже, вероятно, трансвычислительна. В переводе на русский первое означает, приблизительно, что нам не известно способа нахождения её наилучшего решения, кроме перебора всех возможных ответов, а второе – что перебирать нам придётся довольно долго (не менее, чем миллиарды лет). На практике, однако, можно попробовать организовать перебор таким хитрым способом, чтобы постепенно находить всё более хорошие решения и остановиться «по готовности».
Перед тем, как продолжить, замечу, что первым нормальным побуждением здорового человека является попытка проложить оптимальный маршрут самостоятельно, вручную, или хотя бы набросать его крупными мазками, а потом доводить автоматически. Но т.к. в нашем случае цена ребра зависит от его положения в маршруте (т.е. от времени суток), а 51 станция находится на достаточно плотном участке графа (внутри кольца и на нём, включая пересадки), прохождение которого существенно зависит от точки входа и выхода, использовать здравый смысл не так уж просто. Интересно также, что в зависимости от того, собираемся ли мы выходить на каждой станции и ждать следующего поезда, или нет, оптимальный маршрут может быть совершенно разным (т.к. интервалы движения поездов на разных линиях различны).
Но продолжим. Как я уже сказал, можно организовать перебор таким способом, чтобы постепенно находить всё более хорошие решения, и, если нам не нужно гарантий того, что найденное решение самое лучшее, мы можем остановиться в любой момент, когда сочтём, что текущий лучший результат «достаточно хорош» для нас. Один из древних классических подходов в такой ситуации – использование генетических алгоритмов.
Это довольно простая идея времён былой популярности эволюционной теории: опишем каждое решение некоторым вектором («геномом»), сформулируем функцию качества конкретного генома (в нашем случае – время прохождения всего маршрута) и запустим эволюцию: добавим случайные мутации, а то и заставим лучшие из «особей», натурально, спариваться. Несколько тысяч поколений этакой евгеники – и у нас готов неплохой сверхчеловек маршрут.
Но дьявол, как водится, в деталях. Во-первых, надо хорошо выбрать представление информации в геноме. Можно, например, сделать геномом вектор с номерами всех станций в порядке их следования в маршруте. Чем это плохо? Геномы разных маршрутов будут разной длины – им будет неудобно скрещиваться. А ещё среди случайных значений генома будет много невалидных маршрутов – таких, которые не позволяют посетить все станции. Другими словами, в пространстве значений генома концентрация действительно возможных кандидатур будет невысокой – а значит, нам отдельно придётся проверять каждого кандидата на валидность, тратя на это лишнее время.

Гораздо удобнее объявить геномом перестановку длины 200 – т.е. такой вектор длины 200, в котором каждая станция встречается лишь 1 раз. Правда, при таком подходе соседними в маршруте могут оказаться станции, между которыми нет прямого соединения. Не беда – мы можем перейти к полному графу, рассчитав кратчайший маршрут по графу между каждой парой вершин (в лоб это несложно сделать за О(|V|^3) операций, что в нашем случае – не так много). Важно отметить, что этот кратчайший маршрут также может быть различным в разное время суток, с учётом динамики расписания. Поэтому, имеет смысл рассчитать такие таблицы для каждого среза расписания интервалов.
Во-вторых, нужно пошаманить с разными видами мутаций и скрещиваний. Науки тут особо нет, сплошная эмпирика, направленная главным образом на то, чтобы, с одной стороны обеспечить быструю сходимость, а с другой – возможность выбраться из эволюционного тупика локального оптимума. В итоге, я остановился на наборе из следующих преобразований:
• случайная перетасовка случайного интервала генома – это быстрая мутация, но не очень аккуратная, на финальных этапах эволюции она с очень низкой вероятностью может улучшить уже неплохое решение.
• зеркальное отражение случайного интервала генома – может быть полезно для сильных изменений (выхода из локального оптимума), с шансами сохранить некоторый порядок (высокое качество) маршрута в контексте нашей задачи
• перестановка X пар случайных значений в геноме местами – хорошая мутация, но медленная, из тупика на ней не выберешься.
• скрещивание (“crossover”) двух геномов – сначала выбираем точку скрещивания на геноме, отрезаем по ней хвосты наших геномов и меняем их местами. После этого мы можем получить некорректный маршрут – поэтому уникализируем результат и добавляем все потерянные узлы, например, в случайные места генома.
Итого, на каждой итерации мы некоторое подмножество лучших особей подвергаем их различным мутациям и формируем из их потомков новое поколение, досыпая к ним несколько полностью случайных маршрутов, чтобы не пасть жертвами инбридинга. Расчёт такой эволюции длиной в 50000 поколений наколеночным скриптом на питоне занимает на моём домашнем десктопе в среднем 20 минут. А чтобы было не так скучно ждать, можно подглядывать за ним в динамике, отрисовывая лучшую особь каждого, скажем, сотого поколения. Вот небольшая гифка, показывающая фаворитов нескольких первых тысяч поколений в цикле:
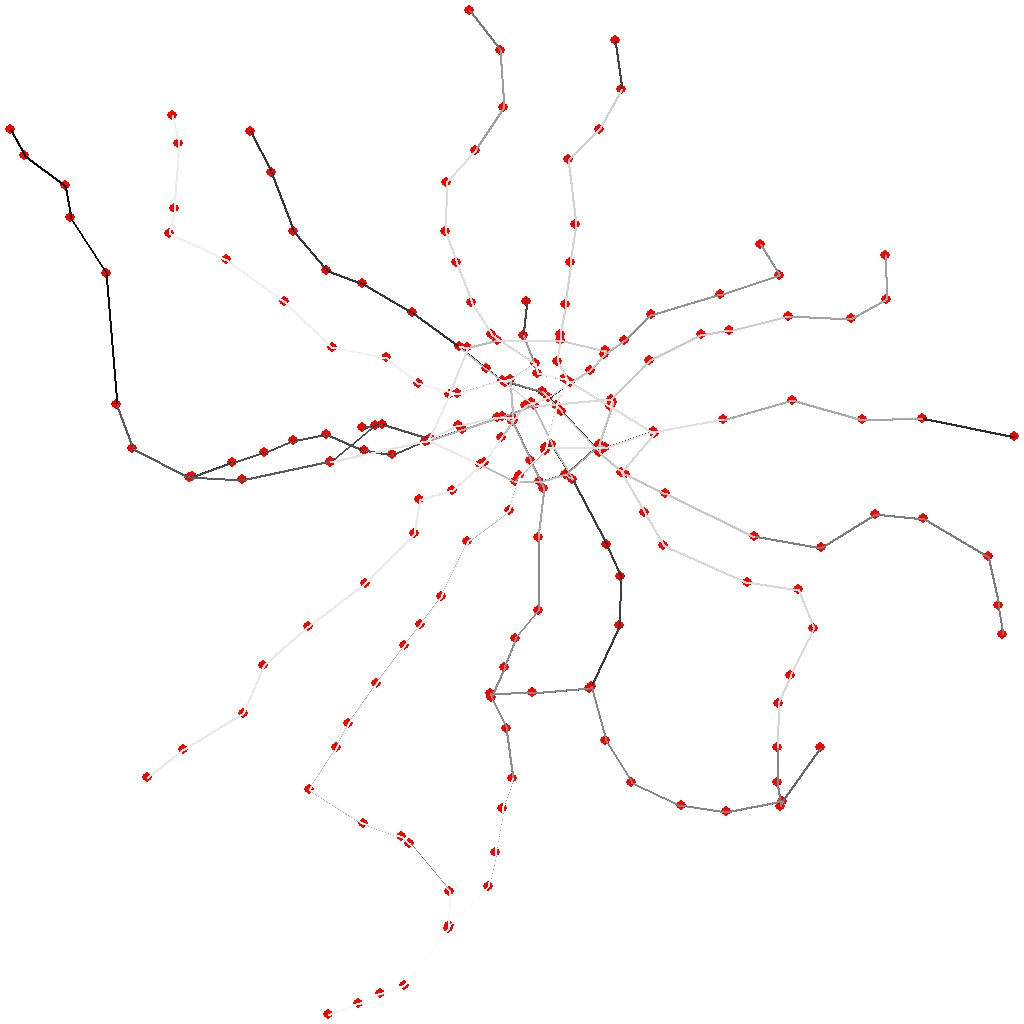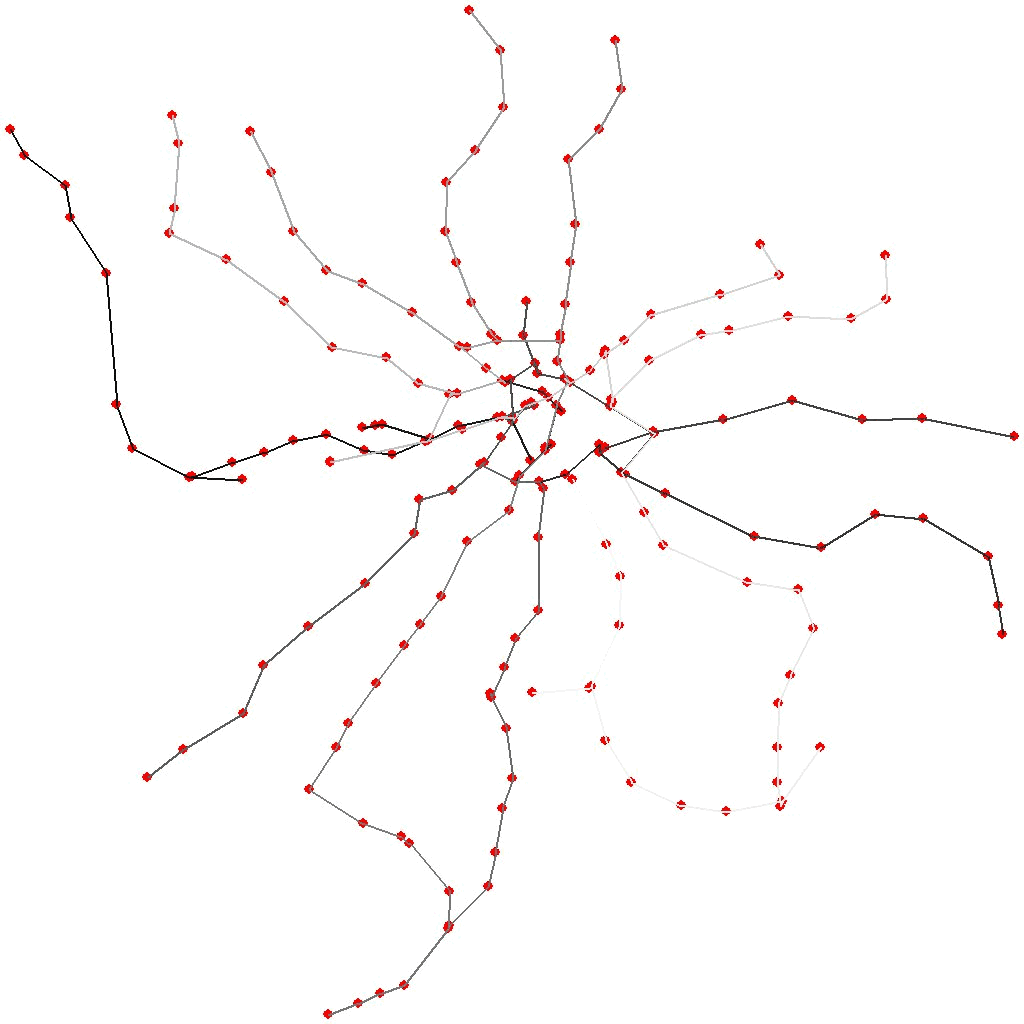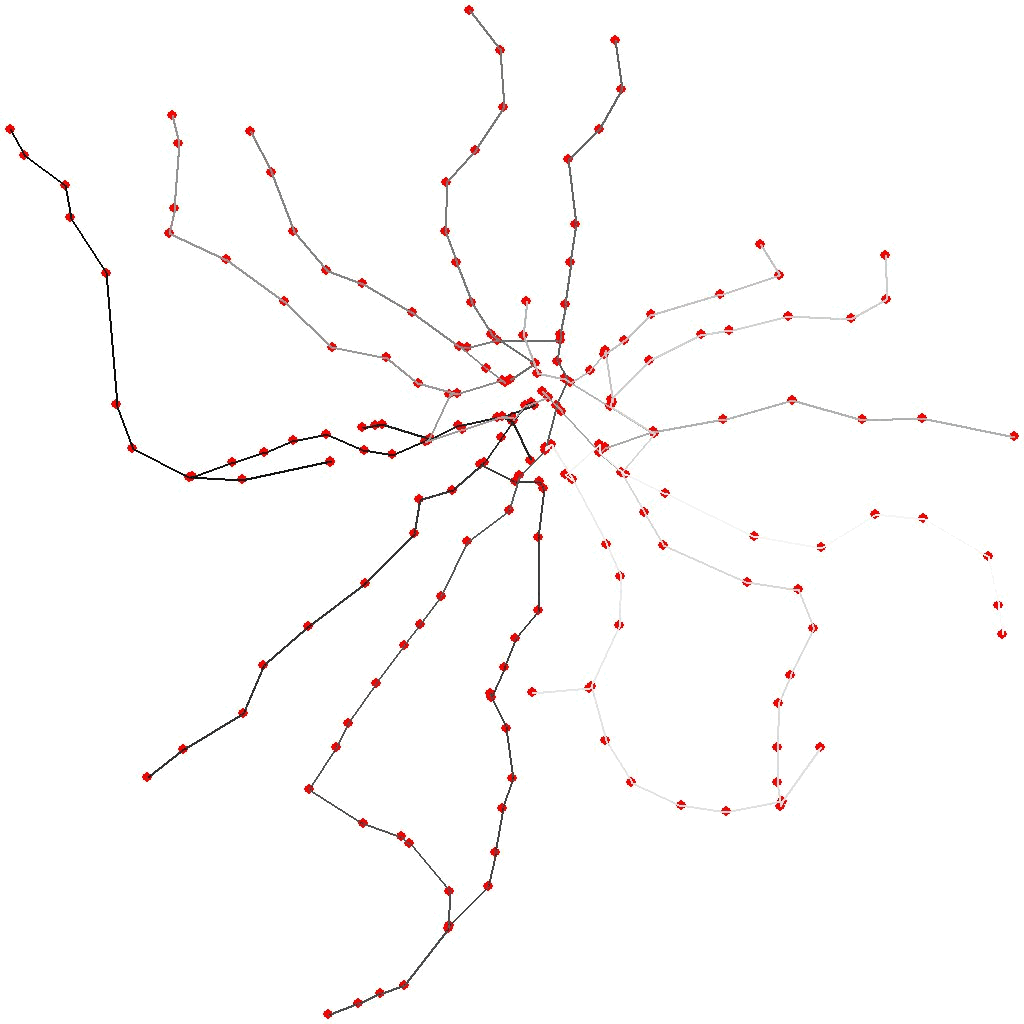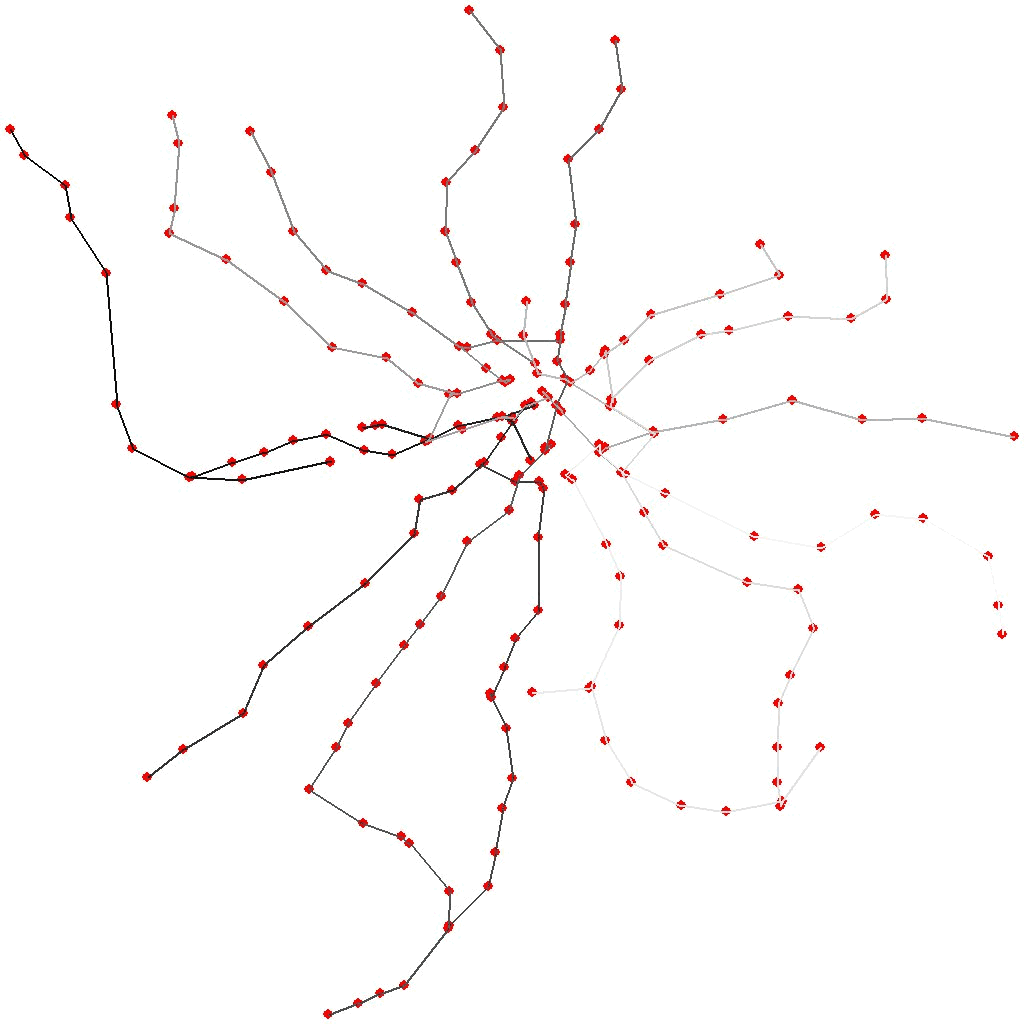
Последовательность шагов в маршруте соответствует градиенту серого. Видно, что в самом начале маршрут меняется достаточно хаотично, потом быстро выходит на локальный оптимум и начинает доводку по мелочам. А если ждать достаточно долго (уже за пределами данной гифки), можно, если повезёт, увидеть, как, время от времени, эволюция перепрыгивает в новый, более глубокий оптимум и продолжает оптимизацию там.
Важный момент – если мы видим, что независимые прогоны оптимизации дают нам существенно разные ответы, пусть и похожие по качеству, значит, велика вероятность того, что мы так и не нашли глобальный оптимум. Но нас устроит и достаточно хорошее его приближение, которое можно попробовать получить «мультистартами» – запустить алгоритм много раз (в т.ч. с разными настройками, например, задавая начало и конец маршрута равными различным фиксированным веткам) и выбирать лучший из наблюдаемых результатов.
Чтобы немного продлить саспенс, покажу вам маршрут, занявший по моим расчётам второе место (ехать от светлого к тёмному):
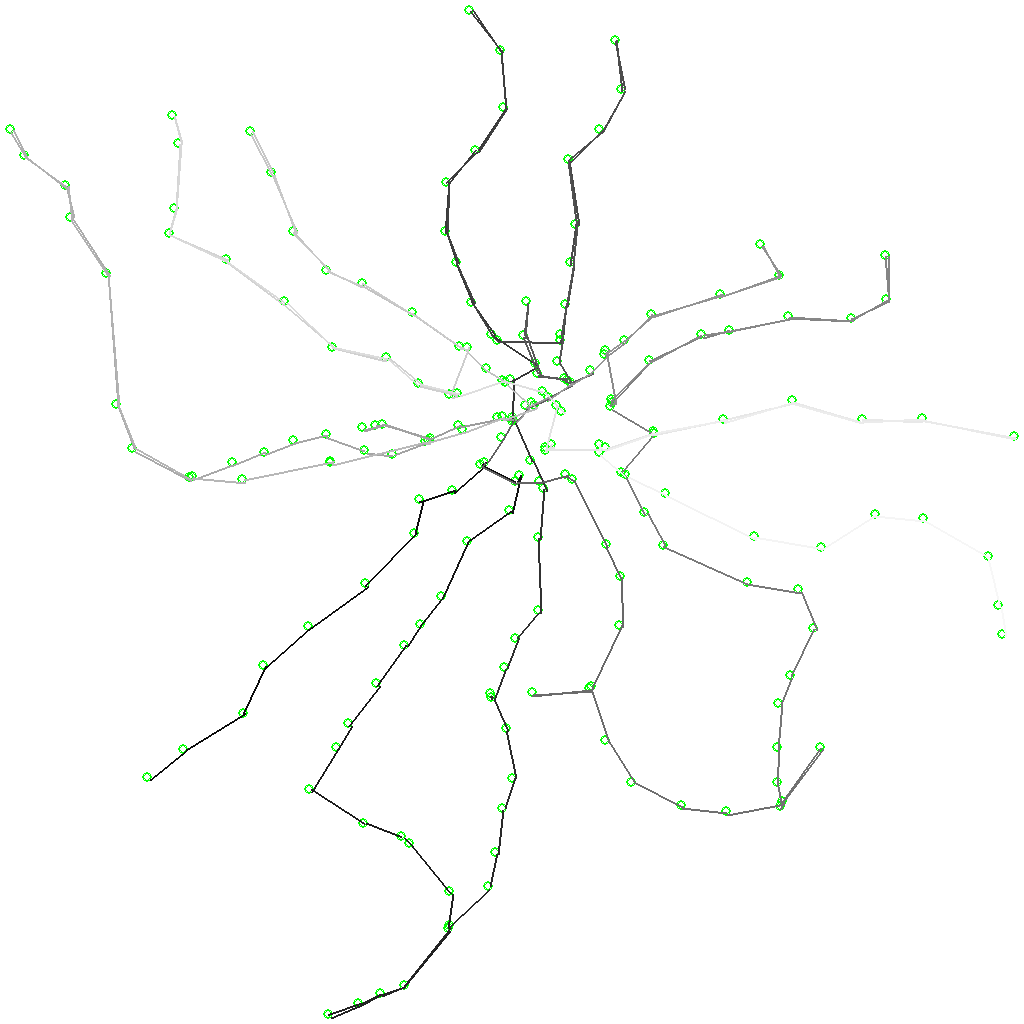
А итоговая оценка длительности самого лучшего маршрута получилась равной 19 часам 51 минуте. Напомню, интервал работы московского метро – примерно 20 часов, а все исходные данные об интервалах следования поездов я взял из любительских замеров. Если бы у меня получился маршрут в 10 или 40 часов – всё было бы, так или иначе, ясно. Но тут запас составлял всего 9 минут при неизвестной (но явно не маленькой) погрешности.
Назад, в реальный мир
Примерно в этот момент идея проверить этот маршрут на практике окрепла. К тому времени несколько моих друзей уже были в курсе моих странных изысканий. Пара из них оказались достаточно безумными, и вот – мы собрали команду для проверки боем. Но, так как риски «не попасть» в отведённое время были довольно высокими, я решил сначала проверить ряд альтернативных вариантов.
Вариант «Вернуть монорельс». Любопытный факт: проезд от Тимирязевской до ВДНХ на метро с пересадкой через кольцо занимает меньше времени, чем с переходом на монорельс и обратно (по данным pMetro, без необходимости выходить на каждой станции). Вариант отвергнут.
Вариант «Добавить наземный транспорт». Идея в том, что можно попробовать перемещаться между конечными разных линий на общественном транспорте по земле. За данными по пересадкам на наземный траспорт я пошёл к Диме Крюкову из Яндекс.Расписаний. Оказалось, что точной информации о пересадках между метро и наземном транспортом у нас сейчас нет, зато есть подробная информация о всех наземных остановках и маршрутах автобусов/троллейбусов/трамваев.
Делать нечего, пришлось делать матчинг остановок со станциями по названиям. Там обнаружилось довольно много подводных граблей, о которых рассказывать не очень интересно. Скажу только, что в Москве нашлось ровно 999 наземных остановок, названных «в честь» той или иной станции метро (не считая нескольких «метромостов», «метродепо», «метрогородков» и прочего). А ещё, некоторые остановки до сих пор названы в честь уже переименованных станций метро. Но это мелочи.
Вот вам, кстати, схема с найденными наземными «хордами»:
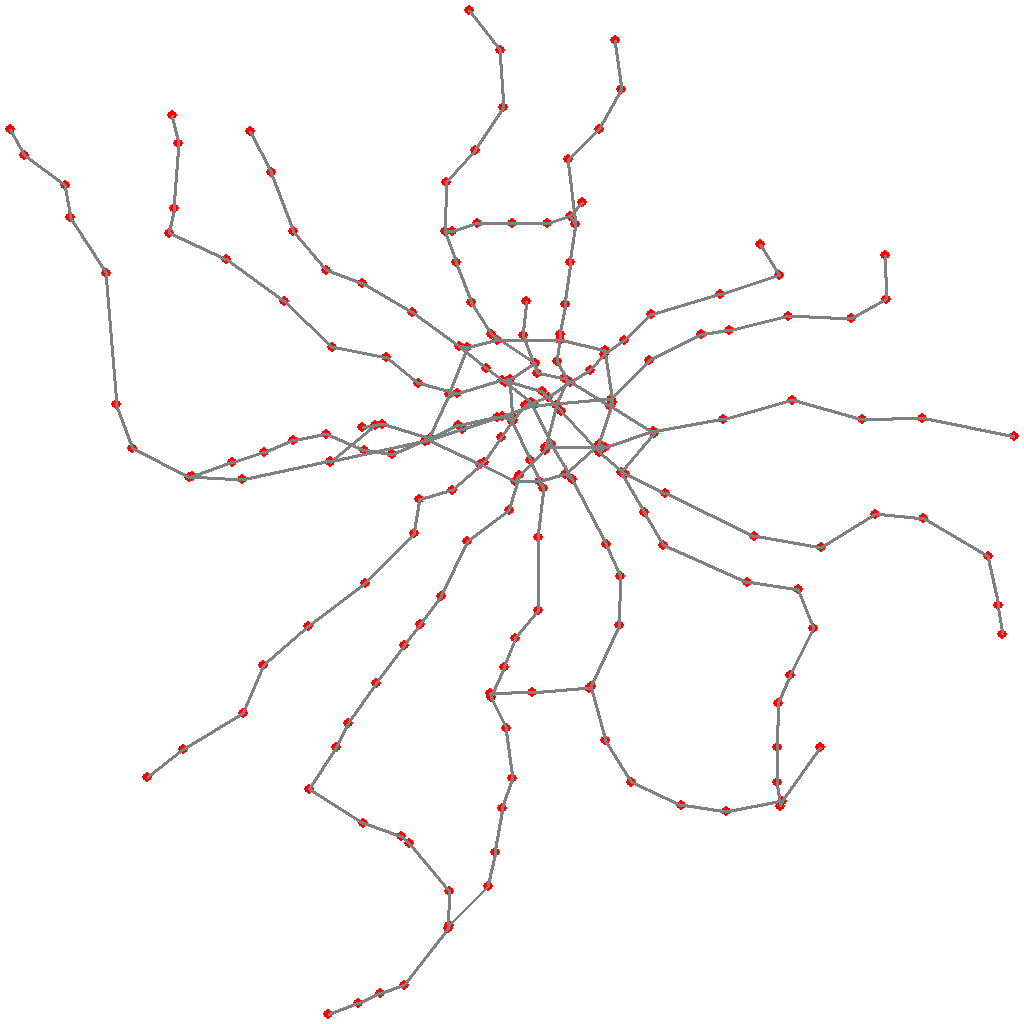
Но, так или иначе, когда я добавил оценки по времени выхода + ожидания наземного транспорта + проезда + возвращения в метро, оказалось, что эти «хорды» не очень помогают – концепция «метро-трипа» теряет исходную чистоту, а расчётный выигрыш составляет всего 15-20 минут. Вариант отвергнут.
Вариант «Добавить такси». По сути, это модификация предыдущего варианта, но вместо общественного транспорта предполагается использование такси. Для этого я руками выбрал для каждой конечной странции каждой радиальной ветки географически ближайшие к ней станции на соседних ветках и добавил для таких пар «хорды» с оценкой времени по Яндекс.Навигатору.
После оптимиазации получился вот такой интересный маршрут с четырьмя «хордами»:

Такой маршрут по расчётам оказался примерно на 30 минут короче, чем мой оптимальный. Вариант отвергнут, как «не спортивный».
Итоги
После бурных дебатов мы решили ехать оптимальный маршрут без «хорд» и с выходом на каждой станции. В конце концов, если б мы хотели просто номинально объехать все станции, можно было бы вообще не выходить из вагона и получить время порядка 12 часов. Но московское метро по праву считается одним из красивейших метрополитенов мира, так что лучше насладиться частью станций, чем посетить все, но не увидеть ничего.
Настрой был серьезным, поэтому на данном этапе мы обратились в Московский метрополитен, и провалидировали с их помощью наш маршрут. Нам выделили специального сопровождающего из Центра обеспечения мобильности пассажиров, разрешили вести фото и видеосъемку и даже позволили изредко пользоваться служебными туалетами, которые, как выяснилось, есть на каждой станции.
Итак, 12 мая мы с товарищами зашли в московское метро ранним утром и, не выбираясь наверх, посетили все 199 доступных в данный момент станций до закрытия метрополитена. Зачем мы всё это сделали – совершенно не ясно, но суть не в этом, главное – нам это удалось.
У нас не было задачи проехать всё метро «на время», скорее мы хотели действительно посмотреть все станции за один день. Мы выходили на каждой станции, делали фотографии (пару сотен фото можно найти в наших различных лентах в соцсетях) и ехали дальше – иногда в том же поезде, а иногда пропуская по несколько поездов к ряду, если станция была настолько интересной, что нам хотелось провести на ней побольше времени.
Наше итоговое время составило 16 часов 22 минуты, и мы с удовольствием публикуем наш маршрут, с тем, чтобы любой желающий мог попробовать улучшить это время.

Я с огромным удовольствием благодарю всех, кто так или иначе помогал нам в этой безумной затее –и саму команду марафонцев, и команду онлайн-сопровождения, и многочисленных людей, помогавших нам в подготовке.
Подробные благодарности можно прочитать в нашем закрывающем посте на ФБ.
Автор: Яндекс







