В современных условиях интерес к анализу данных постоянно и интенсивно растет в совершенно различных областях, таких как биология, лингвистика, экономика, и, разумеется, IT. Основу этого анализа составляют статистические методы, и разбираться в них необходимо каждому уважающему себя специалисту в data mining.
К сожалению, действительно хорошая литература, такая что умела бы предоставить одновременно математически строгие доказательства и понятные интуитивные объяснения, встречается не очень часто. И данные лекции, на мой взгляд, необычайно хороши для математиков, разбирающихся в теории вероятностей именно по этой причине. По ним преподают магистрам в немецком университете имени Кристиана-Альбрехта на программах «Математика» и «Финансовая математика». И для тех, кому интересно, как этот предмет преподается за рубежом, я эти лекции перевел. На перевод у меня ушло несколько месяцев, я разбавил лекции иллюстрациями, упражнениями и сносками на некоторые теоремы. Замечу, что я не профессиональный переводчик, а просто альтруист и любитель в этой сфере, так что приму любую критику, если она конструктивна.
Вкратце, лекции вот о чем:

Условное математическое ожидание
Эта глава не относится непосредственно к статистике, однако, идеальна для старта её изучения. Условное математическое ожидание — это наилучший выбор для предсказания случайного результата на основе уже имеющейся информации. И это тоже случайная величина. Здесь рассматриваются его различные свойства, такие как линейность, монотонность, монотонная сходимость и прочие другие.
Основы точечного оценивания
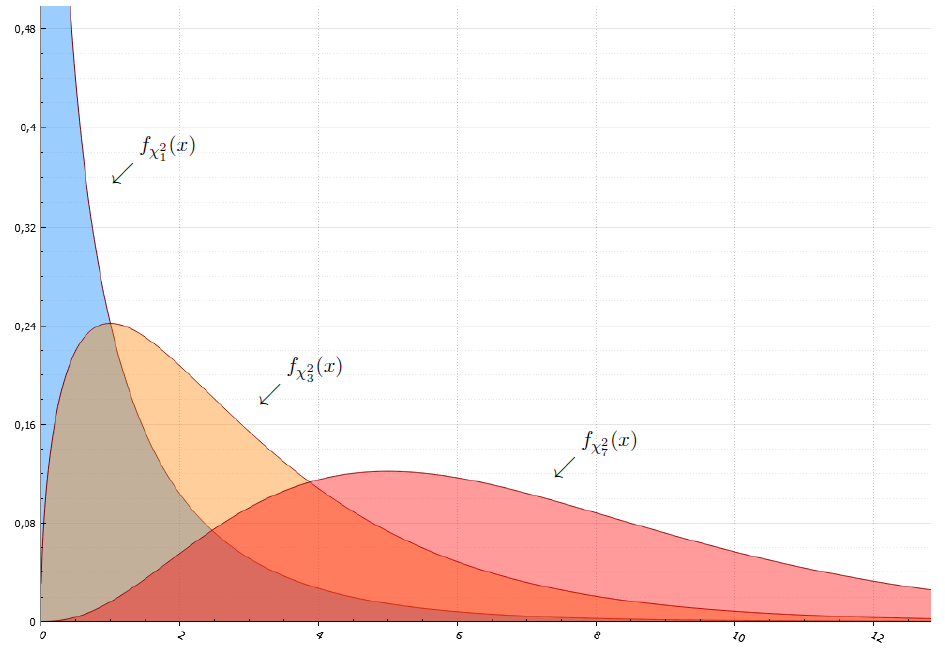
Как оценить параметр распределения? Какой для этого выбрать критерий? Какие методы при этом использовать? Эта глава позволяет ответить на все эти вопросы. Здесь вводятся понятия несмещенной оценки и равномерно несмещенной оценки с минимальной дисперсией. Объясняется, откуда берутся распределение хи-квадрат и распределение Стьюдента, и чем они важны при оценивании параметров нормального распределения. Рассказывается, что такое неравенство Рао-Крамера и информация Фишера. Также вводится понятие экспоненциального семейства, многократно облегчающего получение хорошей оценки.
Байесовское и минимаксное оценивания параметров

Здесь описывается иной философский подход к оценке. В данном случае параметр считается неизвестным потому, что он является реализацией некой случайной величины с известным (априорным) распределением. Наблюдая результат эксперимента мы рассчитываем так называемое апостериорное распределение параметра. На основе этого, мы можем получить Байесовскую оценку, где критерием является минимум потерь в среднем, или минимаксную оценку, минимизирующую максимально возможные потери.
Достаточность и полнота
Эта глава имеет серьезное прикладное значение. Достаточная статистика — это функция от выборки, такая что достаточно хранить только результат этой функции для того, чтобы оценить параметр. Таких функций много и среди них выделяют так называемые минимальные достаточные статистики. Например, для оценки медианы нормального распределения достаточно хранить лишь одно число — среднее арифметическое по всей выборке. Работает ли это также для других распределений, например, для распределения Коши? Как достаточные статистики помогают в выборе оценок? Здесь вы можете найти ответы на эти вопросы.
Асимптотические свойства оценок
Пожалуй, самое важное и необходимое свойство оценки — это её состоятельность, то есть стремление к истинному параметру при увеличении размера выборки. В этой главе рассказывается какими свойствами обладают известные нам оценки, полученные описанными в предыдущих главах статистическими методами. Вводятся понятия асимптотической несмещенности, асимптотической эффективности и расстояния Кульбака-Лейблера.
Основы тестирования
Кроме вопроса о том, как оценить неизвестный нам параметр, мы должны каким-то образом проверить, удовлетворяет ли он требуемым свойствам. Например, проводится эксперимент, в ходе которого испытывается новое лекарство. Как узнать, выше ли вероятность выздоровления с ним, нежели чем с использованием старых лекарств? В этой главе объясняется, как строятся подобные тесты. Вы узнаете, что такое равномерно наиболее мощный критерий, критерий Неймана-Пирсона, уровень значимости, доверительный интервал, а также откуда берутся небезызвестные критерий Гаусса и t-критерий.
Асимптотические свойства критериев
Как и оценки, критерии должны удовлетворять определенным асимптотическим свойствам. Иногда могут возникнуть ситуации, когда нужный критерий построить невозможно, однако, используя известную центральную предельную теорему, мы строим критерий, асимптотически стремящийся к необходимому. Здесь вы узнаете, что такое асимптотический уровень значимости, метод отношения правдоподобия, и как строятся критерий Бартлетта и критерий независимости хи-квадрат.
Линейная модель
Эту главу можно рассматривать как дополнение, а именно, применение статистики в случае линейной регрессии. Вы разберетесь в том, какие оценки хороши и в каких условиях. Вы узнаете, откуда взялся метод наименьших квадратов, каким образом строить критерии и зачем нужно F-распределение.
Ссылки на
Автор: The_Freeman