Интересные алгоритмы кластеризации, часть первая: Affinity propagation

в 5:38, , рубрики: affinity propagation, clustering, data mining, graphs, Алгоритмы, математика, машинное обучение, метки:

Если вы спросите начинающего аналитика данных, какие он знает методы классификации, вам наверняка перечислят довольно приличный список: статистика, деревья, SVM, нейронные сети… Но если спросить про методы кластеризации, в ответ вы скорее всего получите уверенное «k-means же!» Именно этот золотой молоток рассматривают на всех курсах машинного обучения. Часто дело даже не доходит до его модификаций (k-medians) или связно-графовых методов.

Не то чтобы k-means так уж плох, но его результат почти всегда дёшев и сердит. Есть более совершенные способы кластеризации, но не все знают, какой когда следует применять, и очень немногие понимают, как они работают. Я бы хотел приоткрыть завесу тайны над некоторыми алгоритмами. Начнём с Affinity propagation.

image


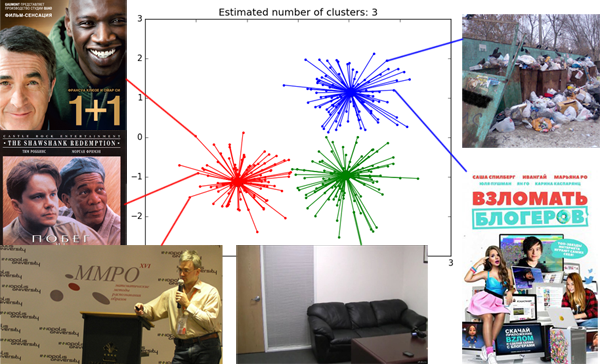
Предполагается, что вы знакомы с классификацией методов кластеризации, а также уже применяли k-means и знаете его плюсы и минусы. Я постараюсь не очень глубоко вдаваться в теорию, а попытаться донести идею алгоритма простым языком.

Affinity propagation

Affinity propagation (AP, он же метод распространения близости) получает на вход матрицу схожести между элементами датасета $textbf{S}=N times N$ и возвращает набор меток, присвоенных этим элементам. Без лишних слов сразу выложу алгоритм на стол:

image

Ха, было бы что выкладывать. Всего три строчки, если рассматривать основной цикл; (4) — явно правило присвоения меток. Но не всё так просто. Большинству программистов совсем не очевидно, что же эти три строчки делают с матрицами $textbf{S}$, $textbf{R}$ и $textbf{A}$. Околоофициальная статья поясняет, что $textbf{R}$ и $textbf{A}$ — матрицы «ответственности» и «доступности» соответственно, и что в цикле происходит «обмен сообщениями» между потенциальными лидерами кластеров и остальными точками. Честно сказать, это весьма поверхностное объяснение, и толком непонятно ни назначение этих матриц ни как и почему изменяются их значения. Попытка разобраться скорее всего приведёт вас куда-нибудь сюда. Хорошая статья, но неподготовленному человеку сложно выдержать целый экран монитора, забитый формулами.

Так что я начну с другого конца.

Интуитивное объяснение

В некотором пространстве, в некотором государстве живут точки. У точек богатый внутренний мир, но существует некоторое правило $s(i, k)$, по которому они могут сказать, насколько похож на них сосед. Более того, у них уже есть таблица $textbf{S}$, где записаны все $s(i, k)$, и она почти никогда не меняется.

Одним жить на свете скучно, поэтому точки хотят собраться в кружки по интересам. Кружки формируются вокруг лидера (exemplar), который представляет интересы всех членов товарищества. Каждая точка хотела бы видеть лидером кого-то, кто максимально на неё похож, но готова мириться с другими кандидатами, если те нравятся многим другим. Следует добавить, что точки довольно-таки скромные: все думают, что лидером должен быть кто-нибудь другой. Можно переформулировать их низкую самооценку так: каждая точка считает, что когда дело доходит до объединения в группы, то она сама на себя не похожа ($s(k, k) < 0$). Убедить точку стать лидером, могут либо коллективные ободрения со стороны похожих на неё товарищей, либо, наоборот, если в обществе не будет совсем никого похожего на неё.

Точки заранее не знают ни что это будут за коллективы, ни общее их количество. Объединение идёт сверху вниз: сначала точки цепляются за президентов групп, затем только размышляют, кто ещё поддерживает того же кандидата. На выбор точки в качестве лидера влияют три параметра: сходство (про него уже сказано), отвественность и доступность. Ответственность (responsibility, таблица $textbf{R}$ c элементами $r(i, k)$) отвечает за то, насколько $i$ хочет видеть $k$ своим предводителем. Ответственность возлагается каждой точкой на кандидата в лидеры группы. Доступность (availability, таблица $textbf{A}$, c элементами $a(i, k)$) — есть ответ от потенциального предводителя $k$, насколько хорошо $k$ готова представлять интересы $i$. Ответственность и доступность точки вычисляют в том числе и сами для себя. Только когда велика самоответственность (да, я хочу представлять свои интересы) и самодоступность (да, я могу представлять свои интересы), т.е. $a(k, k) + r(k, k) > 0$, точка может перебороть врождённую неуверенность в себе. Рядовые точки в конечном итоге присоединяются к лидеру, для которого у них наибольшая сумма $a(i, k) + r(i, k)$. Обычно в самом начале, $textbf{R}=textbf{0}$ и $textbf{A}=textbf{0}$.

Возьмём простой пример: точки X, Y, Z, U, V, W, весь внутренний мир которых — любовь к котикам, $K$. У X аллергия на кошек, для него будем считать $K=-2$, Y относится к ним прохладно, $K=-1$, а Z просто не до них, $K=0$. У U дома четыре кошки ($K=4$), у V — пять ($K=5$), а у W целых сорок ($K=40$). Определим непохожесть как абсолютную величину разности $K$. X непохож на Y на один условный балл, а на U — на целых шесть. Тогда сходство, $s(i, k)$ — это просто минус непохожесть. Получается, что точки с нулевым сходством как раз таки одинаковы; чем более отрицательно $s(i, k)$, тем сильнее отличаются точки. Немного контринтуитивно, ну да ладно. Размер «самонепохожести» в примере оценим в 2 балла ($s(k, k)=-2$).

Итак, на первом шаге каждая точка $i$ возлагает ответственность на всех $k$ (в том числе и на себя) пропорционально сходству между $i$ и $k$ и обратно пропорционально сходству между $i$ и самым похожим на него вектором кроме $k$ ((1) c $a(i,j)=0$). Таким образом:

  • Ближайшая (самая похожая) точка задаёт распределение ответственности для всех остальных точек. Расположение точек дальше первых двух пока что влияет только на $r(i, k)$ отведённую им и только им.
  • Ответственность, возлагаемая на ближайшую точку также зависит от расположения второй ближайшей.
  • Если в радиусе досягаемости $i$ есть несколько более-менее похожих на него кандидатов, на тех будет возложена примерно одинаковая ответственность
  • $s(k, k)$ выступает своего рода ограничителем — если какая-то точка слишком сильно непохожа на все остальные, ей ничего не остаётся, кроме как надеяться только на себя

Если $r(i, k) > 0$, то $i$ хотела бы, чтобы $k$ был её представителем. $r(k, k) > 0$ означает, что сама $k$ хочет быть основателем коллектива, $r(k, k) < 0$ — что $k$ хочет принадлежать другому коллективу.

Возвращаясь к примеру: X возлагает на Y отвественность в размере $inline$-1-(-2)=1$inline$ балл, на Z — $inline$-2-(-1)=-1$inline$ балл, на U — $inline$-6-(-1)=-5$inline$, а на себя $inline$-2-(-1)=-1$inline$. X в общем-то не против, чтобы лидером группы котоненавистников был Z, если Y не захочет быть им, но вряд ли будет общаться с U и V, даже если они соберут большую команду. W настолько непохожа на все остальные точки, что ей ничего не остаётся, как возлагать отвественность в размере $inline$-2-(-35)=33$inline$ балла только на себя.

Затем точки начинают думать, насколько они сами готовы быть лидером (доступны, available, для лидерства). Доступность для самого себя (3) складывается из всей положительной ответственности, «голосов», отданных точке. Для $k$ неважно, сколько точек думают, что она будет плохо их представлять. Для неё главное, что хоть кто-то думает, что она будет их представлять хорошо. Доступность $k$ для $i$ зависит от того, насколько сильно $k$ готов представлять сам себя и от количества положительных отзывов о нём (2) (кто-то другой тоже считает, что он будет отличным представителем коллектива). Эта величина ограничивается сверху нулём, чтобы снизить влияние точек, про которых слишком многие думают хорошо, чтобы они не объединили в одну группу ещё больше точек и цикл не вышел из под контроля. Чем меньше $r(k, k)$, тем больше голосов нужно собрать $k$, чтобы $a(i, k)$ было равно 0 (т.е. эта точка была не против взять под своё крыло ещё и $i$).

Начинается новый этап выборов, но теперь уже $textbf{A} neq textbf{0}$. Вспомним, что $a(k, k) geq 0$, а $a(i, k) leq 0, i neq k$. Это по-разному влияет на $r(i, k)$

  1. $i=k$. Тогда $a(k, k) geq 0$ не играет роли, и в (1) все $inline$-max(dots)$inline$ в правой части будут не меньше, чем были на первом шаге. $a(i, j) < 0$ по сути отдаляет точку $i$ от $j$. Самоответственность точки повышается от того, что у самого лучшего кандидата с её точки зрения, плохие отзывы.
  2. $i neq k$. Тут выступают оба эффекта. Этот случай расщепляется на два:
    • $a(i, j) + s(i, j), i neq j$ — max. То же самое что и в случае 1, но повышается отвественность возлагаемая на точку $k$
    • $a(i, i) + s(i, i)$ — max. Тогда $inline$-max(dots)$inline$ будет не больше, чем на первом шаге, $r(i, k)$ уменьшается. Если продолжать аналогию, то это как если бы точка, которая и так уже задумывалась, не стать ли её лидером, получила дополнительное одобрение.

Доступность оставляет в соревновании точки которые или готовы сами постоять за себя (W, $a(i, i)=0$, но это никак не влияет на (1), т.к. даже с учётом поправки W находится очень далеко от остальных точек) или те, за которых готовы постоять другие (Y, в (3) у неё по слагаемому от X и от Z). X и Z, которые не строго лучше всего похожи на кого-то, но при этом на кого-то таки похожи, выбывают из соревнования. Это влияет на распределение отвественности, что влияет на распределение доступности и так далее. В конце концов, алгоритм останавливается — $a(i, k)$ перестают меняться. X, Y и Z объединяются в компанию вокруг Y; дружат U и V c U в качестве лидера; W хорошо и с 40 кошками.

Перепишем решающее правило, чтобы получить ещё один взгляд на решающее правило алгоритма. Воспользуемся (1) и (3). Обозначим $tilde s(i, k)=a(i, k) + s(i, k)$ — сходство с поправкой на то, что $k$ говорит о своих командирских способностях $i$; $tilde d(i, k)=- tilde s(i, k)$ — непохожесть $i$ -$k$ с поправкой.

image

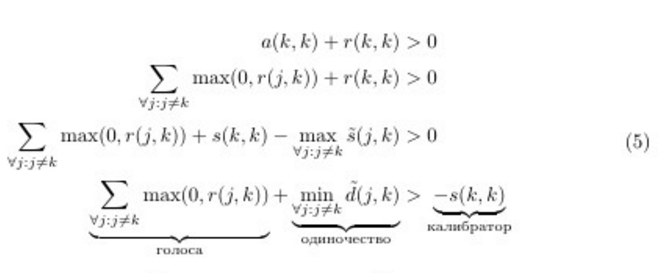
Примерно то, что я сформулировал вначале. Отсюда видно, что чем менее уверены в себе точки, тем больше «голосов» необходимо собрать или тем более непохожим на остальные нужно быть, чтобы стать лидером. Т.е. чем меньше $s(k, k)$, тем крупнее получаются группы.

Что ж, я надеюсь, вы приобрели некоторое интуитивное представление того, как работает метод. Теперь чуть серьёзнее. Давайте поговорим про нюансы применения алгоритма.

Очень-очень краткий экскурс в теорию

Кластеризацию можно представить в виде задачи дискретной максимизации с ограничениями. Пусть на множестве элементов задана функция сходства $s(i, j)$. Наша задача найти такой вектор меток $mathbf{c}={c_1, c_2 ... c_N}, c_i in {1 dots N}$, который максимизирует функцию

$S(c)=sum^N_{i=1}{s(i, c_i)} + sum^N_{k=1}{delta(c_k)}$

где $delta(c_k)$ — член ограничитель, равный $inline$-infty$inline$, если существует точка $i$, которая выбрала точку $k$ своим лидером ($c_i=k$), но сама $k$ лидером себя не считает ($c_k neq k$). Плохая новость: нахождение идеального $mathbf{c}$ — это NP-сложная задача, известная как задача о размещении объектов. Тем не менее, для её решения существует несколько приближённых алгоритмов. В интересующих нас методах $s_i$, $c_i$ и $delta_i$ представляются вершинами двудольного графа, после чего между ними происходит обмен информации, позволяющий с вероятностной точки зрения оценить, какая метка лучше подойдёт для каждого элемента. См. вывод здесь. Про распространение сообщений в двудольных графах см. здесь. Вообще распространение близости — это частный случай (скорее, сужение) циклического распространения убеждений (loopy belief propagation, LBP, см. здесь), но вместо суммы вероятностей (подтип Sum-Product) в некоторых местах мы берём только максимальную (подтип Max-Product) из них. Во-первых, LBP-Sum-Product на порядок сложнее, во-вторых, там легче столкнуться с вычислительными проблемами, в-третьих теоретики утверждают, что для задачи кластеризации это имеет больший смысл.

Авторы AP при много говорят про «сообщения» от одного элемента графа к другому. Такая аналогия происходит из вывода формул через распространение информации в графе. На мой взгляд она немного путает, ведь в реализациях алгоритма никаких сообщений «точка-точка» нет, зато есть три матрицы $textbf{S}$, $textbf{R}$ и $textbf{A}$. Я бы предложил следующую трактовку:

  1. При вычислении $r(i, k)$ идёт пересылка сообщений от точек данных $i$ к потенциальным лидерам $k$ — мы просматриваем матрицы $textbf{S}$ и $textbf{A}$ вдоль строк
  2. При вычислении $a(i, k)$ идёт пересылка сообщений от потенциальных лидеров $k$ ко всем остальным точкам $i$ — мы просматриваем матрицы $textbf{S}$ и $textbf{R}$ вдоль столбцов

Affinity propagation детерминирован. Он имеет сложность $O(N^2T)$, где $N$ — размер набора данных, а $T$ — количество итераций, и занимает $O(N^2)$ памяти. Существуют модификации алгоритма для разреженных данных, но всё равно AP сильно грустнеет с увеличением размера датасета. Это довольно серьёзный недостаток. Зато распространение близости не зависит от размерности элементов данных. Пока что не существует распараллеленного варианта AP. Тривиальное же распараллеливание в виде множества запусков алгоритма не подходит в силу детерминированности. В официальном FAQ, написано, что вариантов с добавлением данных в реальном времени тоже нет, но я нашёл вот такую статью.

Существует ускоренный вариант AP. Предложенный в статье метод основывается на идее, что необязательно вычислять вообще все обновления матриц доступности и ответственности, ведь все точки в гуще других точек относятся к далёким от них экземплярам примерно одинаково.

Если вам хочется экспериментов (так держать!), я бы предложил поколдовать над формулами (1-5). Части $max{(0, x)}$ в них выглядят подозрительно похоже на нейронно-сеточные ReLu. Интересно, что получится если использовать ELu. Кроме того, раз вы теперь понимаете суть происходящего в цикле, вы можете добавить в формулы дополнительные члены, ответственные за необходимое вам поведение. Таким образом можно «подтолкнуть» алгоритм в сторону кластеров определённого размера или формы. Также можно наложить дополнительные ограничения, если известно, что какие-то элементы с большей вероятностью принадлежат одному множеству. Впрочем, это уже спекуляции.

Обязательные оптимизации и параметры

Affinity propagation, как многие других алгоритмов, можно прервать досрочно, если $textbf{R}$ и $textbf{A}$ перестают обновляться. Для этого почти во всех реализациях используется два значения: максимальное количество итераций и период, с которым проверяется величина обновлений.

Affinity propagation подвержен вычислительным осцилляциям в случаях, когда есть несколько хороших разбиений на кластеры. Чтобы избежать проблем, во-первых, в самом начале к матрице сходства добавляется немного шума (очень-очень немного, чтобы не повлиять на детерменированность, в sklearn-имплементации порядка $10^{-16}$), а во-вторых, при обновлении $textbf{R}$ и $textbf{A}$ используется не простое присваивание, а присваивание с экпоненциальным сглаживанием. Вторая оптимизация притом в целом хорошо влияет на качество результата, но из-за неё увеличивается количество необходимых итераций $T$. Авторы советуют использовать параметр сглаживания $0.5 leq gamma < 1.0$ со значением по умолчанию в $0.5$. Если алгоритм не сходится или сходится частично, следует увеличить $gamma$ до $0.9$ или до $0.95$ с соответствующим увеличением количества итераций.

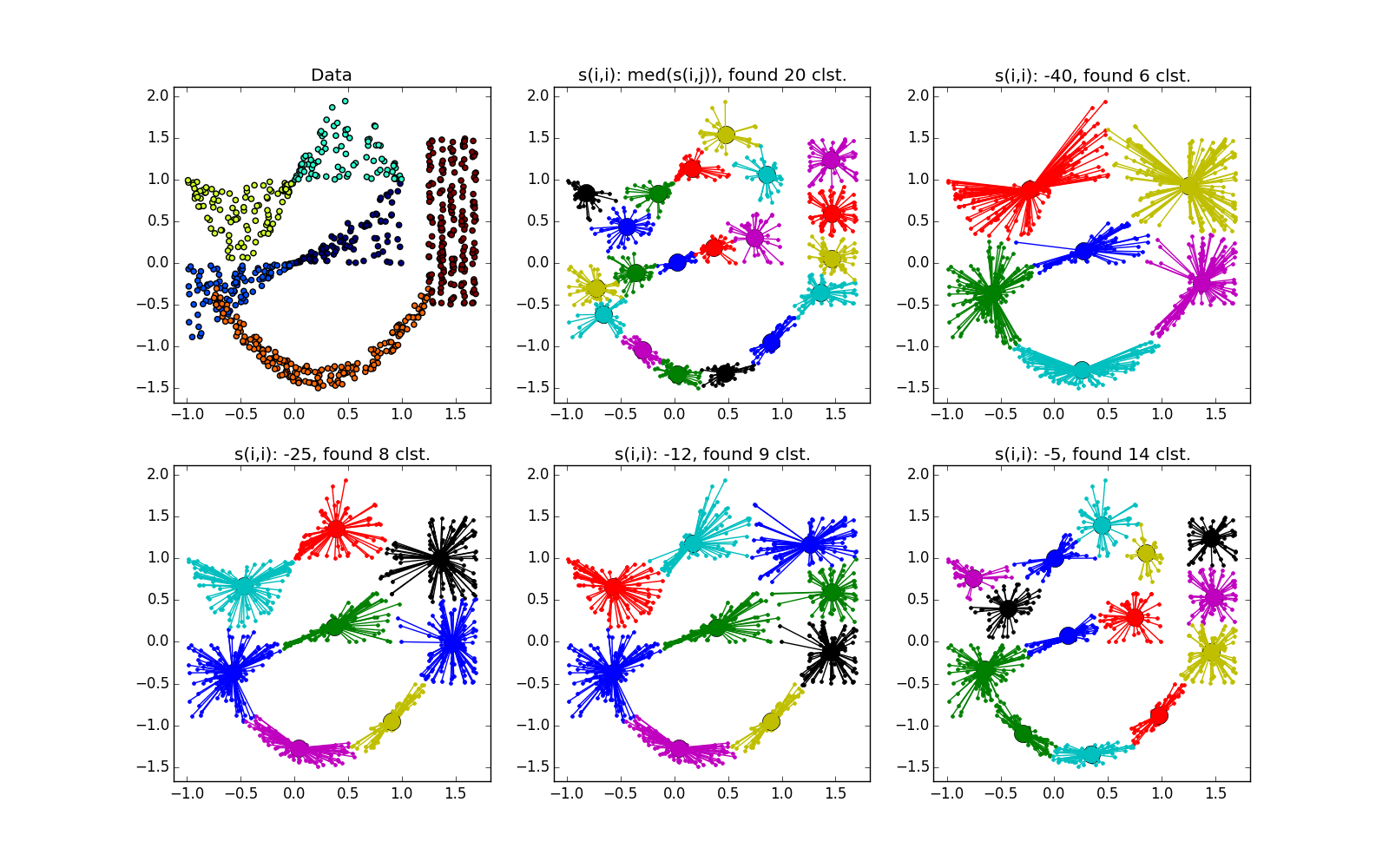
Вот так выглядит отказ — куча мелких кластеров, окружённая кольцом кластеров среднего размера:

image

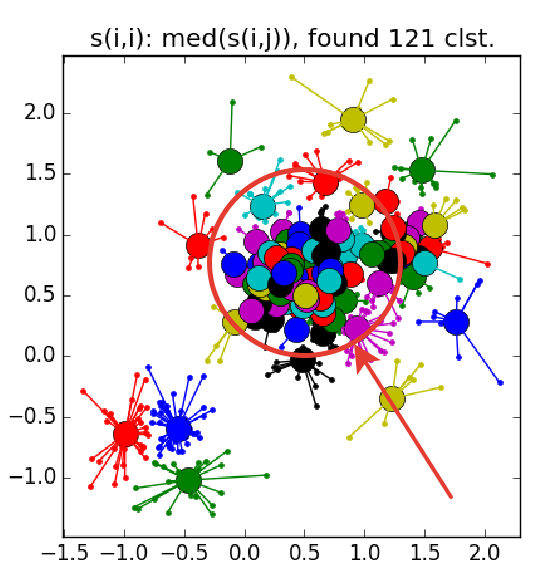
Как уже было сказано, вместо наперёд заданного количества кластеров используется параметр «самоподобия» $s(k, k)$; чем меньше $s(k, k)$, тем крупнее кластеры. Существуют эвристики для автоматической подстройки значения этого параметра: используйте медиану по всем $s(i, k)$ для большего числа кластеров; 25 перцентиль или даже минимум по $s(i, k)$ — для меньшего (всё равно придётся подгонять, ха-ха). При слишком маленьком или слишком большом значении «самоподобия» алгоритм и вовсе не выдаст каких-то полезных результатов.

В качестве $s(i, k)$ само собой напрашивается использовать отрицательное евклидово расстояние между $i$ и $j$, но вас никто не ограничивает в выборе. Даже в случае датасета из векторов действительных чисел можно перепробовать много интересного. Вообще же, авторы утверждают, что на функцию сходства не наложено каких-либо особых ограничений; даже не обязательно, чтобы выполнялось правило симметрии или правило треугольника. Но стоит заметить, что чем более хитроумная у вас $s(i, j)$, тем меньше вероятность, что алгоритм сойдётся к чему-то интересному.

Размеры кластеров, полученных в ходе распространения близости, варьируются в довольно небольших пределах, и если в датасете есть сильно различные по размеру скопления, AP может либо пропустить маленькие, либо посчитать большие за несколько. Обычно вторая ситуация менее неприятна — она исправима. Поэтому часто AP нуждается в постобработке — дополнительной кластеризации лидеров групп. Подходит любой другой метод, тут может помочь дополнительная информация о задаче. Следует помнить, что честным одиноко стоящим точкам выделяется свои кластеры; такие выбросы нужно отфильтровывать перед постобработкой.

Эксперименты

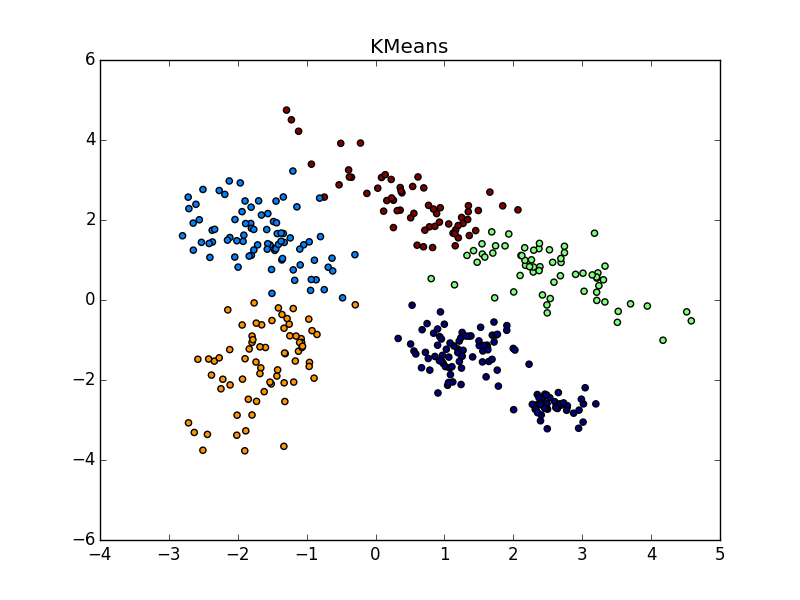
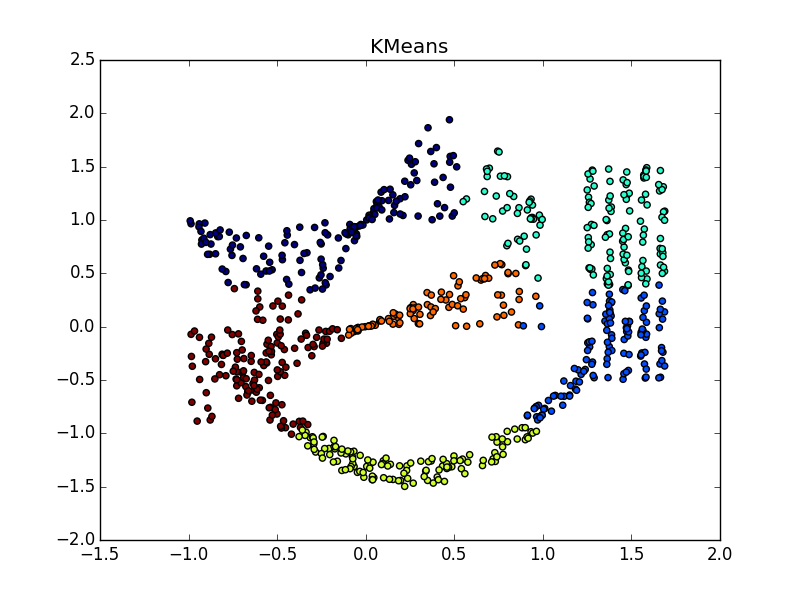
Фух, закончилась стена текста, началась стена картинок. Проверим Affinity propagation на разного вида кластерах.

Стена картинок

Распространение близости неплохо работает на кластерах в виде складок размерности меньше размерности данных. AP обычно не выделяет всю складку, а разбивает её на мелкие куски-субкластеры, которые потом придётся склеивать воедино. Впрочем, это не так уже и сложно: с двадцатью точками это проще, чем с двадцатью тысячами, плюс у нас есть дополнительная информация о вытянутости кластеров. Это намного лучше, чем k-means и многие другие неспециализированные алгоритмы.

image
image
image
image

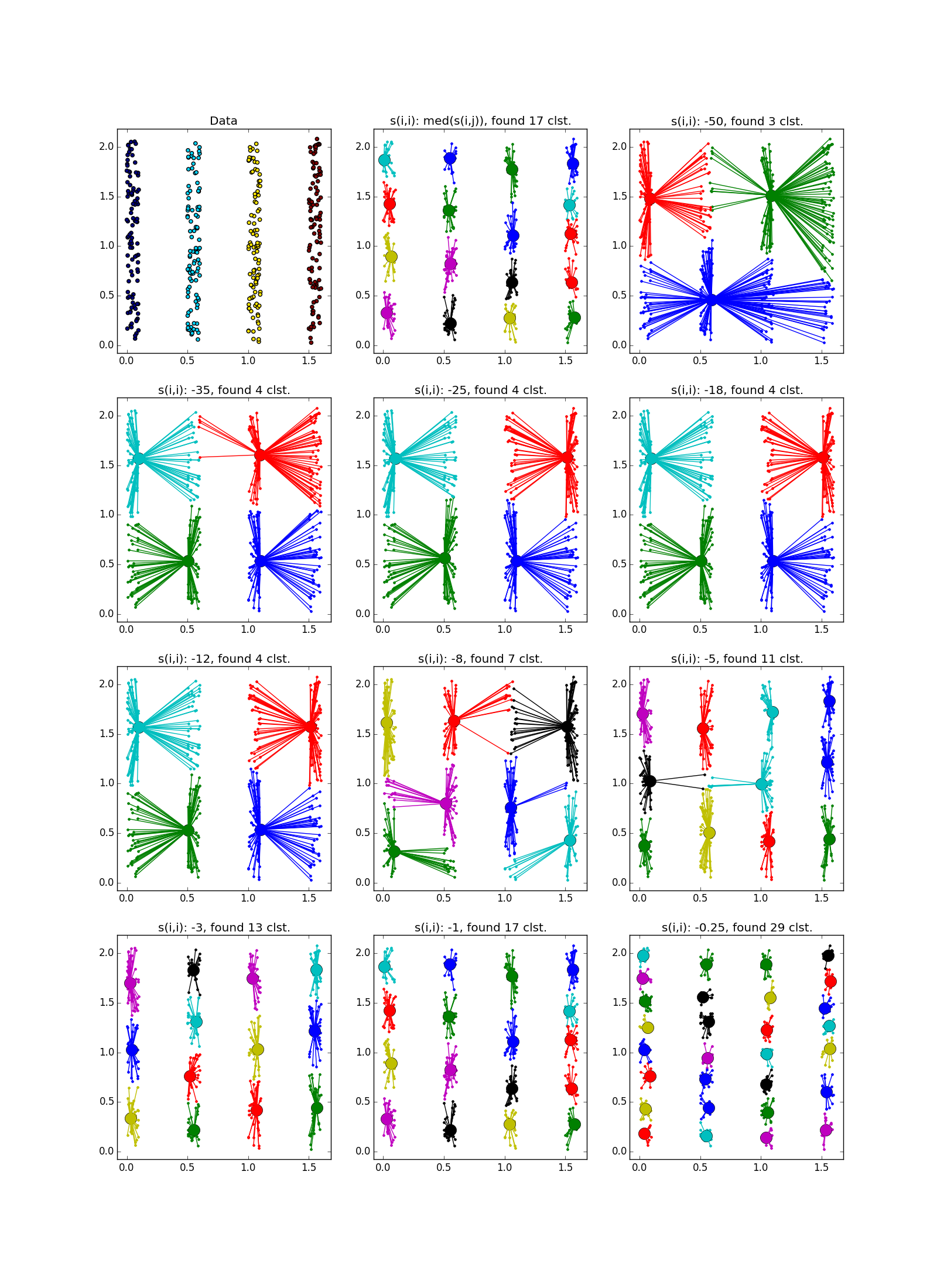
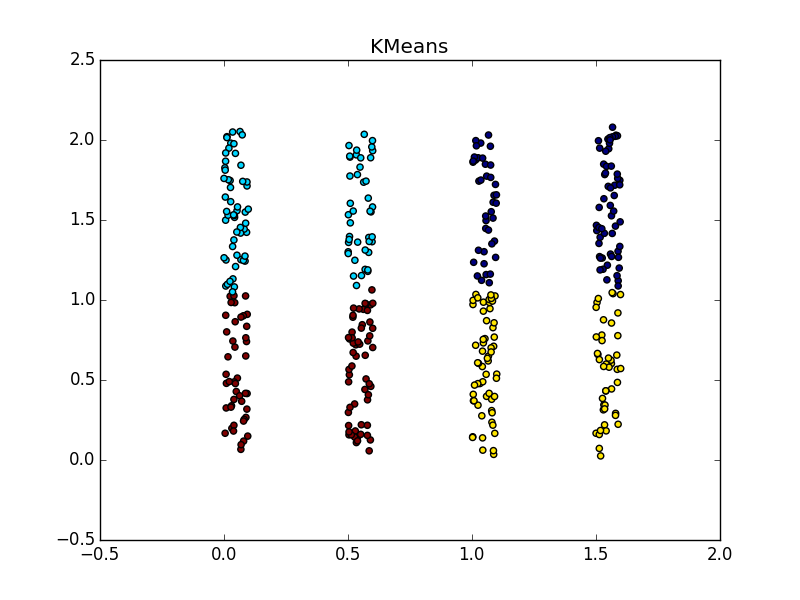
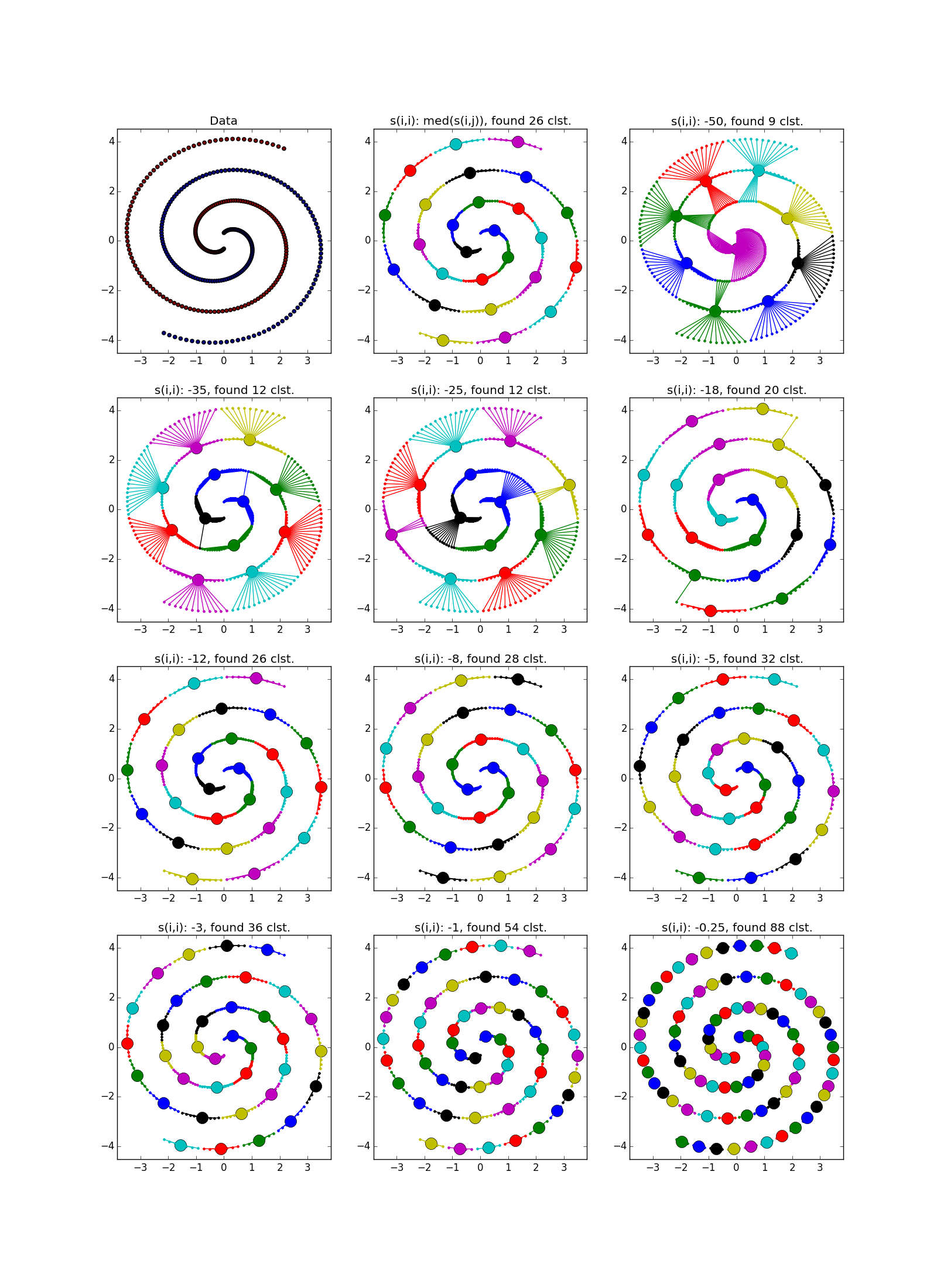
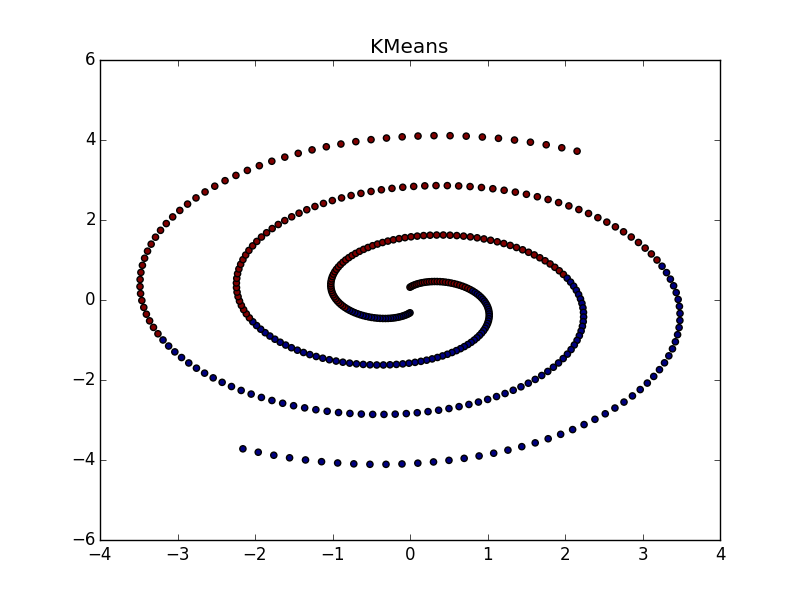
Если складка пересекает другой сгусток, дело обстоит хуже, но даже так AP помогает понять, что в этом месте творится что-то интересное.

image
image

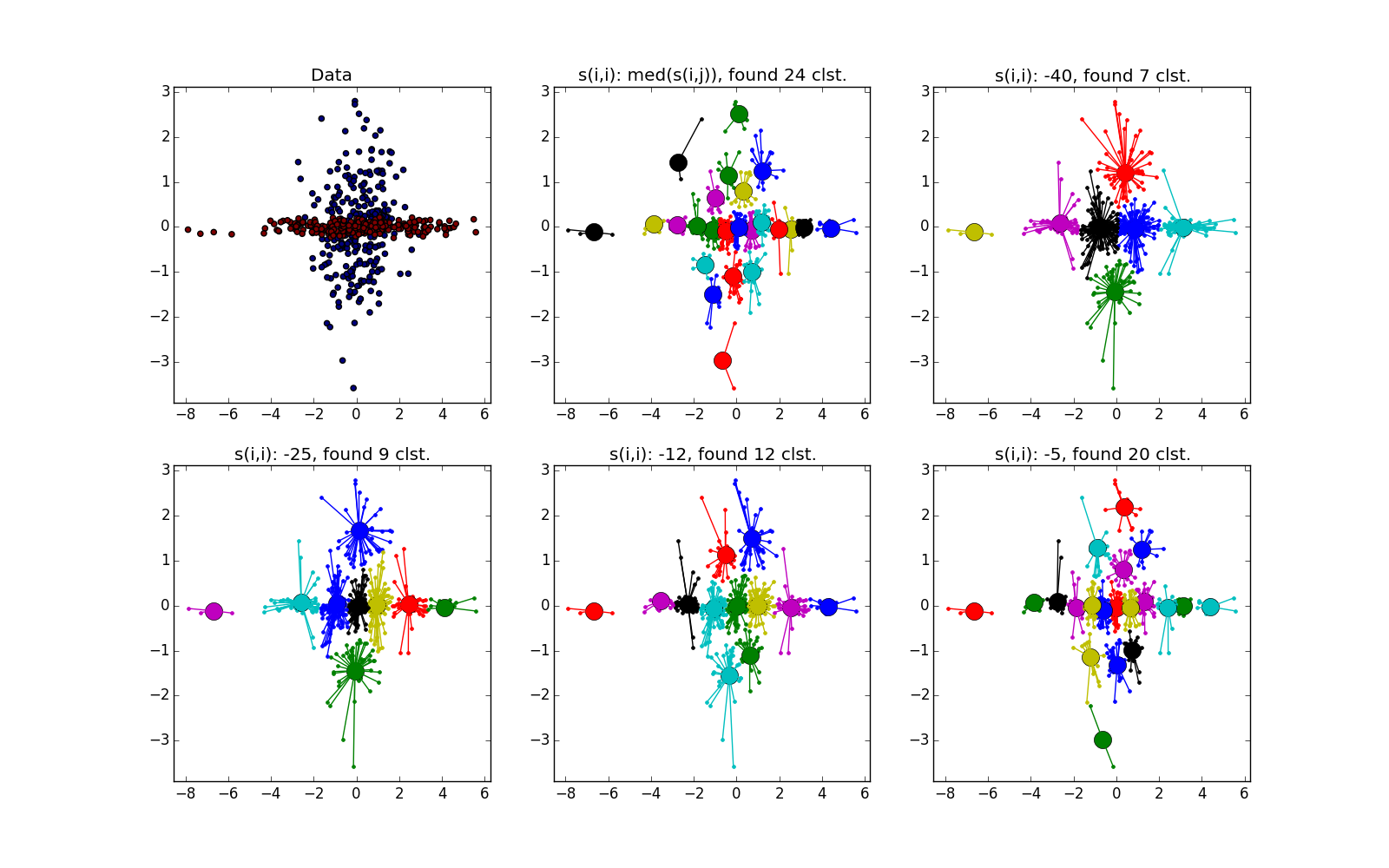
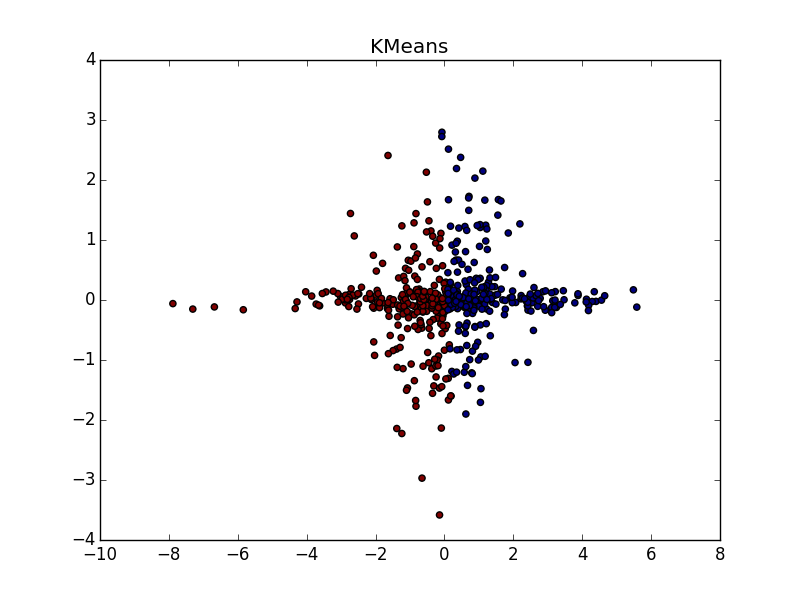
При хорошем подборе параметра и кластеризатора-постобработчика AP выигрывает и в случае кластеров разного размера. Обратите внимание на картинку с $s(i, i)=-8$ — почти идеальное разбиение, если объединить кластеры сверху-справа.

image
image

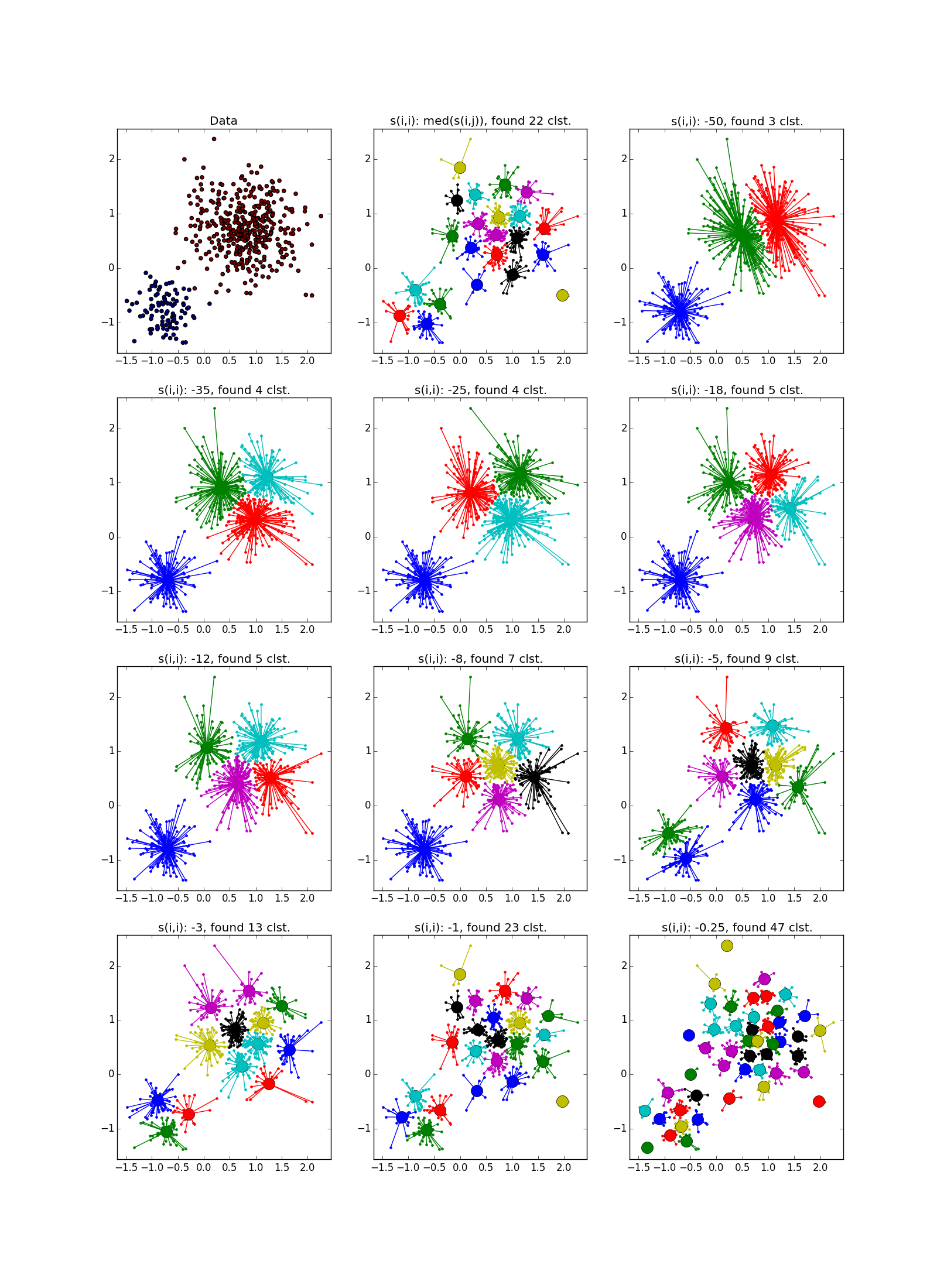
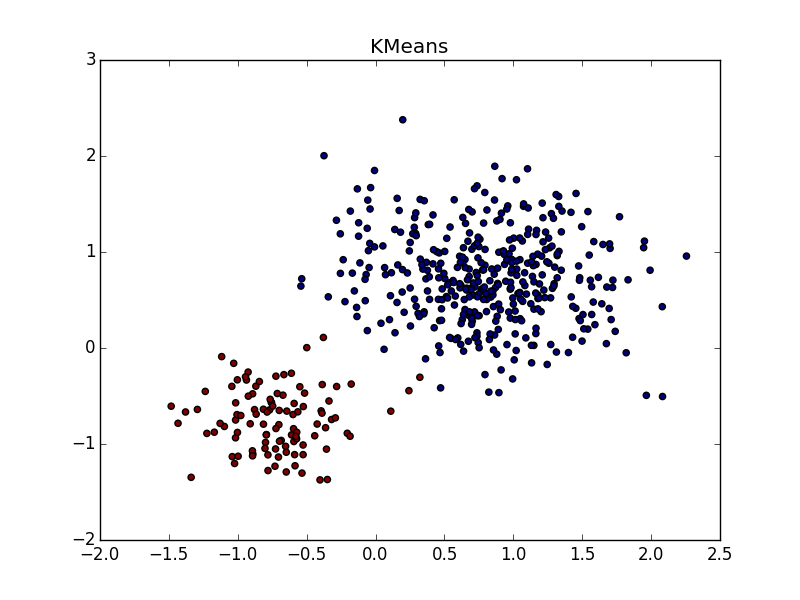
С кластерами одинаковой формы, но разной плотности у AP и k-means плюс-минус паритет. В одном случае нужно хорошо угадать $s(i, i)$, а в другом — $k$.

image
image

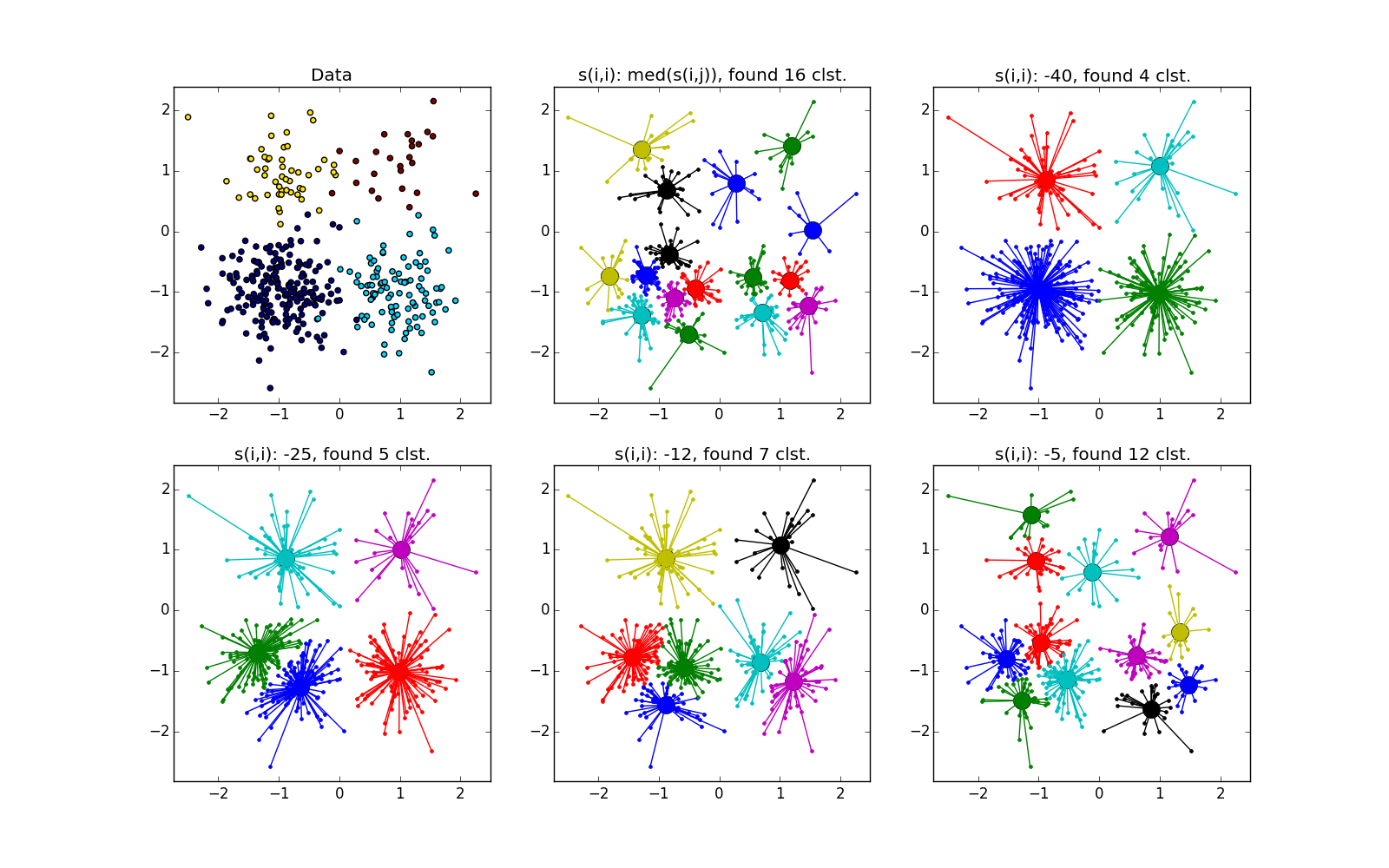
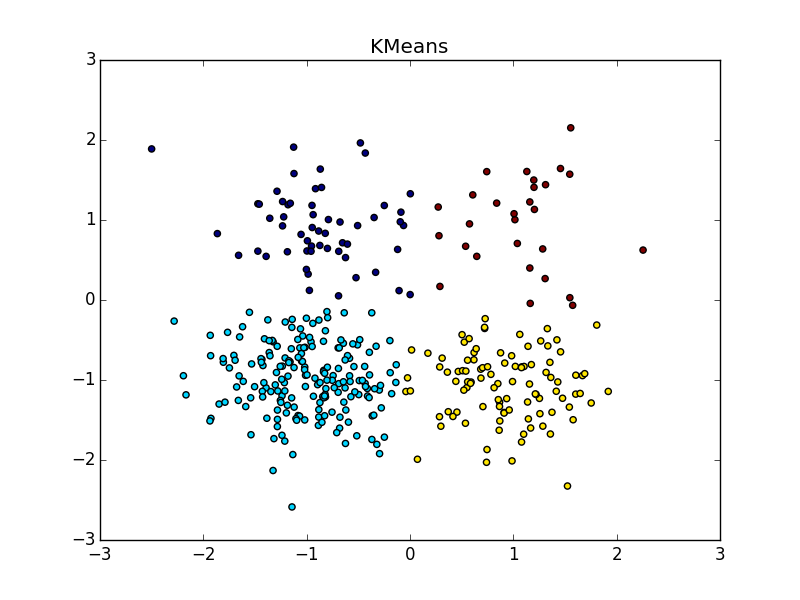
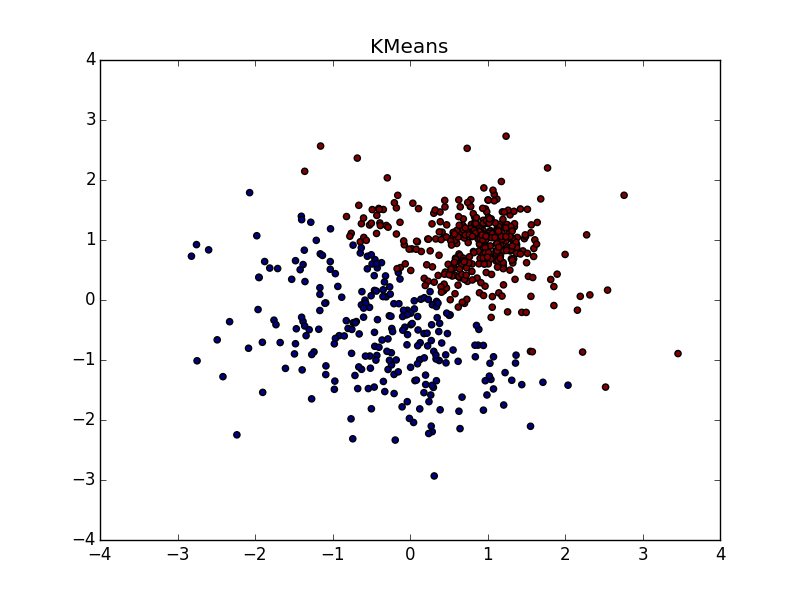
Со сгустком большей плотности в другом сгустке, на мой взгляд, чуть-чуть выигрывает k-means. Он, конечно, «отъедает» значительный кусок в пользу кластера большей плотности, но по визуальному результату работы AP вообще не слишком видно неоднородность.

image
image

Ещё немного картинок:

image
image
image
image

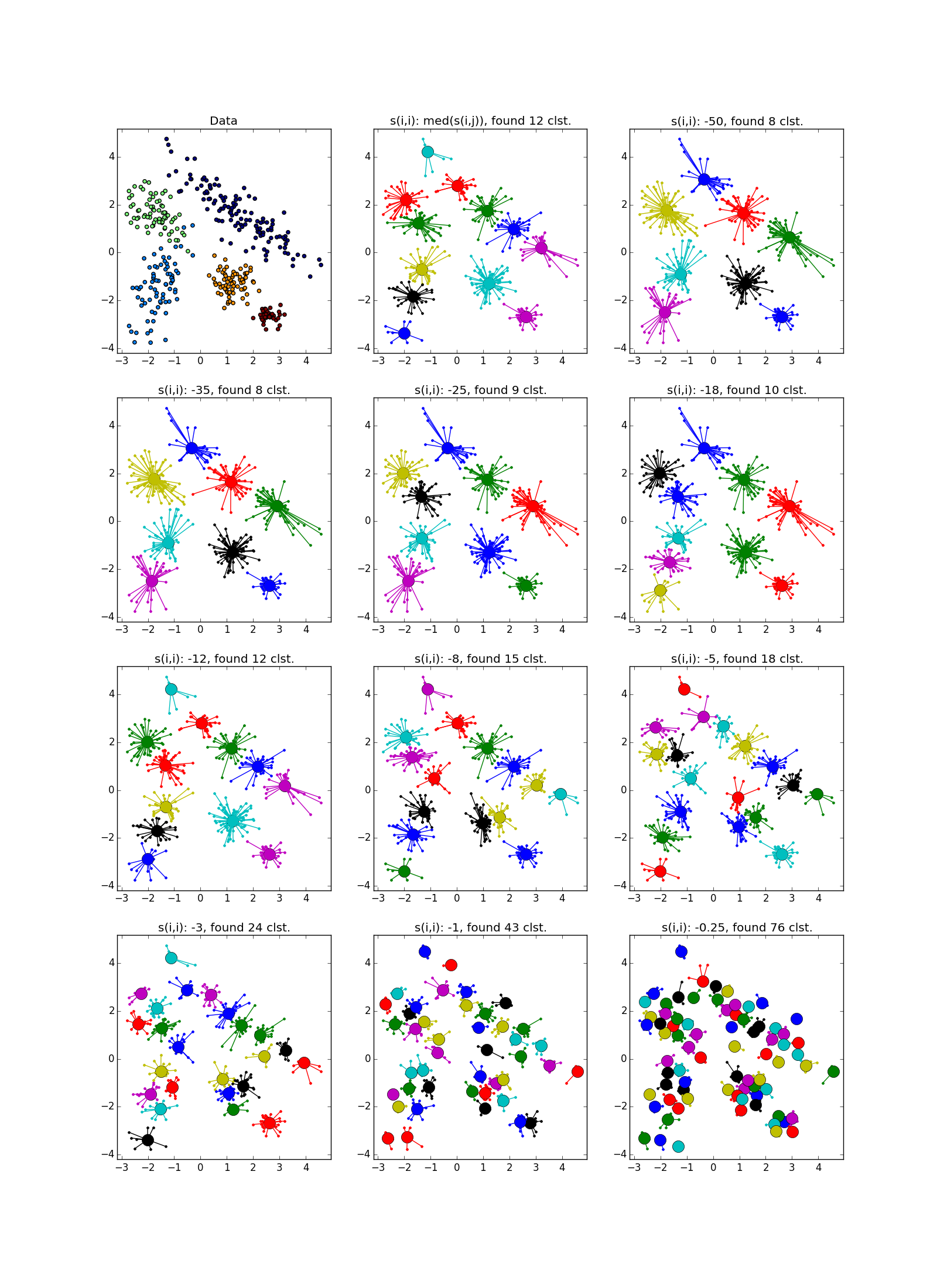
Итог

Используйте Affinity propagation, когда

  • У вас не очень большой ($N < 10^5 - 10^6$) или в меру большой, но разреженный ($N < 10^6 - 10^7$) датасет
  • Заранее известна функция близости
  • Вы ожидаете увидеть множество кластеров различной формы и немного варьирующимся количеством элементов
  • Вы готовы повозиться с постобработкой
  • Сложность элементов датасета значения не имеет
  • Свойства функции близости значения не имеют
  • Количество кластеров значения не имеет

Утверждается, что разные учёные успешно применяли Affinity propagation для

  • Сегментирования изображений
  • Выделения групп в геноме
  • Разбиения городов на группы по доступности
  • Кластеризации образцов гранита
  • Группирования фильмов на Netflix

Во всех этих случаях был получен результат лучше, чем при помощи k-means. Не то чтобы это какой-то суперский результат само по себе. Мне неизвестно, проводилось ли во всех этих случаях сравнение с другими алгоритмами. Я планирую сделать это в грядущих статьях. По всей видимости, на датасетах из реальной жизни больше всего помогает умения распространения близости обходиться с кластерами разной геометрической формы.

Что же, вроде бы и всё. В следующий раз рассмотрим ещё какой-нибудь алгоритм и сравним его с методом распространения близости. Удачи!

Автор: Siarshai

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js