Всем привет! Со школы, решая квадратичные уравнения ( КУ ), например $inline$x^2+x+1=0$inline$, получал корни обладающие мнимой составляющей, $inline$x=-frac{1}{2}pm i frac{sqrt3}{2}$inline$, и при желании увидеть как график пересекает ось $inline$Y$inline$ в точках $inline$x=-frac{1}{2}pm i frac{sqrt3}{2}$inline$, в интернете находил графики вроде:
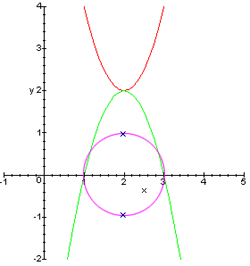
Как график с мнимой частью выглядит ( по моим размышлениям ) в 3D ($inline$Xbot Ybot I$inline$), и есть тема данной статьи.
PS: Под катом тяжёлые анимации
Как обычно, график ф-кции состоит из точек, а точки строятся по пересечению осей $inline$X$inline$ и $inline$Y$inline$.
График ф-ции с комплексной составляющей $inline$Y_{complex}=F(X_{complex})$inline$,
где $inline$X_{complex}=X_{re}+X_{im}=$inline$ $inline$begin{bmatrix}X_{re} \X_{im}end{bmatrix}$inline$ — вектор
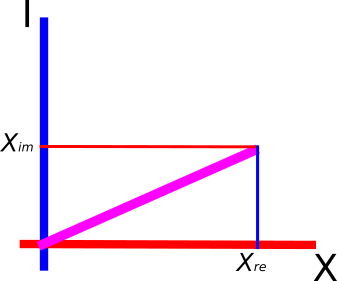
$inline$Y_{complex}=Y_{re}+Y_{im}=begin{bmatrix}Y_{re} \Y_{im}end{bmatrix}$inline$ — вектор
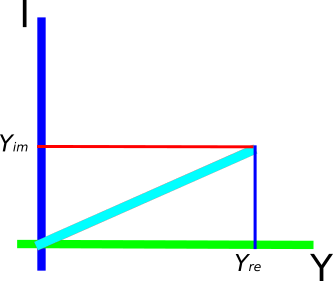
$inline$X_{complex}$inline$ можно представить в виде 3-х мерного вектора $inline$begin{bmatrix}X_{re} \ 0 \X_{im}end{bmatrix}$inline$
$inline$[X_{re}] - ось X$inline$
$inline$[0] - ось Y$inline$
$inline$[X_{im}] - ось I$inline$
Аналогично $inline$Y_{complex}begin{bmatrix}0\ Y_{re} \Y_{im}end{bmatrix}$inline$
$inline$[0] - ось X$inline$
$inline$[Y_{re}] - ось Y$inline$
$inline$[Y_{im}] - ось I$inline$
Точка пересечения $inline$X_{complex}$inline$ и $inline$Y_{complex}$inline$ будет равна сумме векторов $inline$X_{complex}$inline$ и $inline$Y_{complex}$inline$
$inline$begin{bmatrix}X_{re} \ 0 \X_{im}end{bmatrix}$inline$+$inline$begin{bmatrix}0\ Y_{re} \Y_{im}end{bmatrix}$inline$=$inline$begin{bmatrix}X_{re} \ Y_{re} \X_{im}+Y_{im}end{bmatrix}$inline$
С пересечением разобрался.
Далее для построения графика нужно определиться с изменением $inline$X_{re}$inline$ и $inline$X_{im}$inline$ вдоль оси $inline$X_{complex}$inline$, для этого нужен корень КУ. Есть два варианта:
- Сделать $inline$X_{im}$inline$ константой и изменять только $inline$X_{re}$inline$ из корня КУ;
- Получить угол между $inline$X_{re}$inline$ и $inline$X_{im}$inline$ из корня КУ и перемещаться вдоль $inline$X_{complex}$inline$, наращивая $inline$X_{re}$inline$, $inline$X_{im}$inline$ вычислять с учётом угла и $inline$X_{re}$inline$.
Я выбрал второй вариант. Возьмём, для примера:
$inline$x^2+x+1=0$inline$
Корни КУ
$inline$X_{1}=-0.5 + 0.866 i$inline$
$inline$angle=300°$inline$
$inline$X_{2}=-0.5 - 0.866 i$inline$
$inline$angle=60°$inline$
Когда $inline$angle=300°$inline$
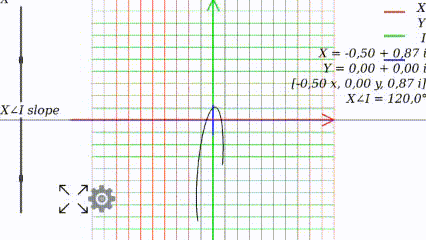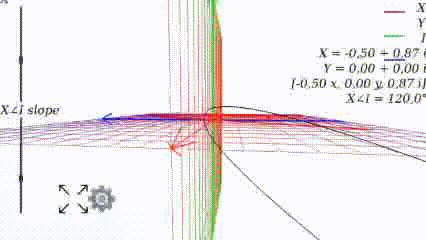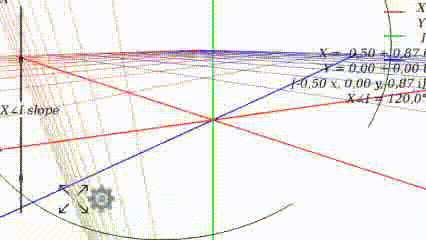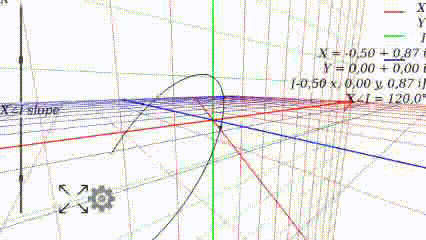
Когда угол равен 0, то график выглядит как привычно выглядел в школе:
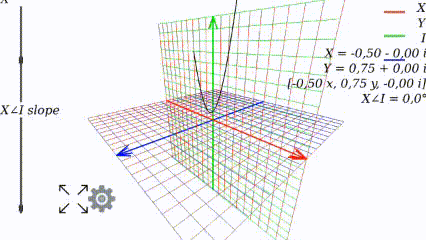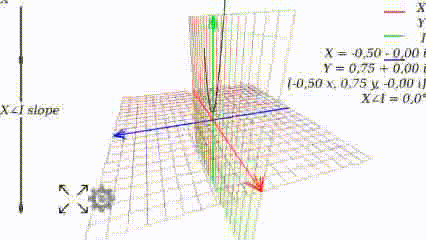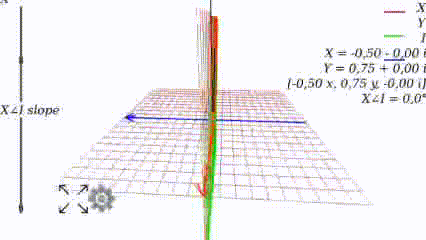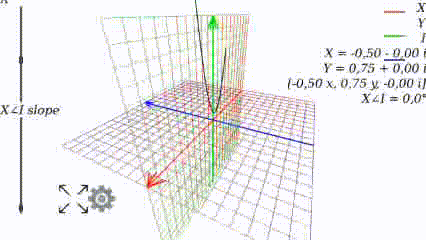
Меняя угол, видим как меняется график:

PS: Представленные графики и их анимации были созданы в приложении «Quadratic Complex 3D Graph» из Google Apps.
Автор: Sorbo


