Оценка связанности событий с помощью Байеса

2017-06-30 в 6:28, admin, рубрики: Алгоритмы, байесовский подход, вероятность, Занимательные задачки, математика, оценка связанности событий

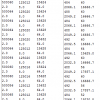
В своей книге Нейт Сильвер приводит такой пример: допустим требуется разместить инвестиции в нескольких предприятиях, которые могут обанкротиться с вероятностью $5%$ . Требуется оценить свои риски. Чем выше вероятность банкротства, тем меньше мы будем вкладывать денег. И наоборот, если вероятность банкротства стремится к нулю, то можно инвестировать без ограничений.

Если имеется 2 предприятия, тогда вероятность того, что они оба обанкротятся и мы потеряем все вложения $P=0.05 cdot 0.05=0.0025$ . Так учит стандартная теория вероятности. Но что будет, если предприятия связаны и банкротство одного ведет к банкротству другого?

Крайним случаем является ситуация, когда предприятия полностью зависимы. Вероятность двойного банкротства $ P$ ( банкрот1 & банкрот2 ) = $P$ ( банкрот1 ), тогда вероятность потери всех вложений равна $P=0.05$ . Методика оценки риска имеет большой разброс $P$ от 0.05 до 0.0025 и реальное значение зависит от того насколько правильно мы оценили связанность двух событий.

Оценка связанности событий с помощью Байеса - 7
При оценке инвестиций в $N$ предприятий имеем $P$ от $0.05$ до $0.05^N$ . То есть максимальная возможная вероятность остается большой $P=0.05$ и старая поговорка «не клади яйца в одну корзину» не сработает, если упадет прилавок со всеми корзинами сразу.

Таким образом наши оценки имеют колоссальный разброс, и сколько куда вкладывать остается вопросом. А ведь надо хорошо считать, прежде чем вкладывать. Нейт Сильвер говорит, что незнание этих простых законов аналитиками привело к крахам фондового рынка в 2008 году, когда рейтинговые агенства США оценивали риски, но не оценивали связанность рисков. Что в конце концов привело к эффекту домино, когда сначала свалился крупный игрок и увлек за собой других.

Попробуем разобрать эту проблему, решив простую математическую задачу после ката.

Давайте решим упрощенную задачу, чтобы научиться оценивать связанность двух событий методом Байеса на простом примере двух монет. Далее математика… Постараюсь разжевать, чтобы самому аж понятно стало.

Пусть имеются 2 монеты $M1$ и $M2$ , которые выдают 0 или 1 при бросании и возможна одна из 4х комбинаций на один бросок:
комбинация 1: 00
комбинация 2: 01
комбинация 3: 10
комбинация 4: 11

Здесь первая цифра относится к первой монете, а вторая ко второй. Я ввел такие обозначения для удобства изложения.

По условию задачи пусть первая монета независима. То есть $P_1(0)=0.5$ и $P_1(1)=0.5$ . А вторая может быть зависима, но мы не знаем насколько сильно. То есть $P_2$ зависит от $P_1$ .

Может есть какой-то магнит, который притягивает монеты, или бросающий является шулером и прохиндеем, коих пруд пруди. Наше незнание мы будем оценивать в виде вероятности.
Оценка связанности событий с помощью Байеса - 19
Чтобы оценить связанность нужен фактический материал и модель, параметры которой будем оценивать. Давайте используем самые простые допущения, чтобы прочувствовать тему и построить модель.

Если монеты несвязны, то все четыре комбинации будут равновероятны. Тут возникает поправка из стандартной теории вероятности — такого результата можно добиться при бесконечном количестве бросаний. Но так как на практике количество бросаний конечно, то мы можем попасть в отклонение от среднего. Например, можно получить нечаянно серию трёх или пяти орлов при подбрасывании монет, хотя в среднем при бесконечном бросании будет точно 50% орлов и точно 50% решек. Отклонение можно инерпретировать как проявление связанности, а можно инерпретировать как обычное отклонение статистики от среднего. Чем меньше выборка, тем больше возможно отклонение, и поэтому можно спутать разные допущения.

Вот тут и приходит на помощь теория Байеса, которая дает возможность оценить вероятность той или иной гипотезы по конечному набору данных. Байес производит обратный процесс от того, с которым мы привыкли иметь дело в теории вероятности. По Байесу оценивается вероятность что наши домыслы совпадают с реальном положении дел, а не вероятность исходов.

Переходим к творческом процессу построения модели. К модели связанности предъявляется требование, — она как минимум должна охватывать возможные варианты. В нашем случае крайними вариантами являются полная связанность или полная независимость монет. То есть модель должна иметь как минимум один параметр k, описывающий связанность.

Опишем её в виде коэффициента $k in [0,1]$ . Если вторая монета всегда полностью совпадает с первой, то $k=$ 1. Если вторая монета всегда имеет противоположные значения, то $k=0$ . Если монеты несвязны, тогда $k=0.5$ . Получается неплохо — одним числом описываем множество вариантов. К тому же смысл этой переменной определяем как вероятность совпадения.

Попробуем оценить это число по фактическим данным.

Пусть имеется конкретный набор данных $D$ , который состоит из $N=5$ исходов:
исход 1: 00
исход 2: 01
исход 3: 11
исход 4: 00
исход 5: 11

На первый взгляд ни о чем не говорит. Количество комбинаций:
$N(00)=2, N(01)=1, N(10)=0, N(11)=2$

Неспешно разберем, что значит формула Байеса. Используем стандартную запись, где знак $|$ означает вероятность выполнения события, если уже известно, что другое событие выполнилось.

$P( k | D)=frac{ P(D | k) cdot P(k) }{P(D)}$

$k=argmax P( k | D )$

В данном случае имеем комбинацию непрерывных и дискретных распределений. $P( k | D )$ и $P(k)$ являются непрерывными распределениями. А $P( D | k)$ и $P(D)$ являются дискретными. Для формулы Байеса такая комбинация возможна. Для экономии времени не расписываю все тонкости.

Если мы будем знать эту вероятность, то можно найти значение $k in [0,1]$ , при котором вероятность нашей гипотезы максимальна. То есть найти наиболее вероятный коэффициент $k$ .

В правой части имеем 3 члена, которые нужно оценить. Проанализируем их.

1)Требуется знать или вычислить вероятность получения таких данных при той или иной гипотезе $P( D | k )$ . Ведь даже если объекты несвязны ( $k=0.5$ ), то получить серию ${00, 00, 00}$ можно, хотя сложно. Намного вероятнее получить такую комбинацию, если монеты связаны ( $k=1$ ). $P( D | k )$ — наиболее важный член и ниже разберем как его вычислять.

2) Необходимо знать $P(k)$ . Вот тут натыкаемся на тонкий момент моделестроения. Мы не знаем эту функцию и будем строить предположения. Если нет дополнительных знаний, то будем считать, что $k$ равновероятно в диапазоне от 0 до 1. Если бы мы имели инсайдерскую информацию, то больше знали бы о связанности строили бы более точный прогноз. Но так как такой информации не имеется, то положим $ k sim равномерно[0,1] $ . Так как эта величина не зависит от $k$ , то при вычислении $k$ она не будет иметь значения.

3) $P(D)$ в данном примере равно константе. Это вероятность иметь такой набор данных, если все величины случайны. Мы можем получить данный набор при разных $k$ с разной вероятностью. Поэтому в общем случае учитываются все возможные пути получения набора $D $ . Так как на этом этапе еще неизвестно значение $k$ , то надо в общем случае проинтегрировать по $P(D)=int_{0}^{1} P(D|k) P(k) dk$ . Так как эта величина не зависит от $k$ , то при вычислении $k$ она не будет иметь значения. (* параграф исправлен на основе замечения Arastas)

Разберем, как вычислять $P( D | k )$ . Помним, что первая монета независима, а вторая зависима. Поэтому вероятность значения для первой монеты будет выглядеть как-то так $P( M1=0 )$ , а для второй монеты так $P( M2=0 | M1=0 )$ . Вероятность совпадения с первой монетой равна $k$ , а вероятность несовпадения равна $(1-k)$ .

Разберем возможные случаи для одного исхода:
$P(00)=P(M1=0) cdot P(M2=0 | M1=0 )=0.5 k$
$P(01)=P(M1=0) cdot P(M2=1 | M1=0 )=0.5 (1-k)$
$P(10)=P(M1=1) cdot P(M2=0 | M1=1 )=0.5 (1-k)$
$P(11)=P(M1=1) cdot P(M2=1 | M1=1 )=0.5 k$

Для проверки сложим вероятности, должна получиться единица $P(00)+P(01)+P(10)+P(11)=0.5 k + 0.5 (1-k) + 0.5 (1-k) + 0.5 k=1$ . Это радует.

Теперь можно перейти к поиску наиболее вероятного значения $k$ по вымышленному набору данных, который уже приводился выше $D={00,01,11,00,11}$ .

Вероятность иметь такой набор
$P( D | k )=P(00) cdot P(01) cdot P(11) cdot P(00) cdot P(11) $ ,
раскрываем
$P( D | k )=(0.5 k) cdot (0.5 (1-k)) cdot (0.5 k) cdot (0.5 k) cdot (0.5 k) $ ,
упрощаем
$P( D | k )=0.5 ^5 cdot k^1 cdot (1-k)^4$ ,
обобщаем для произвольного набора данных
$P( D | k )=0.5^{N} cdot k^{N(00)} cdot k^{N(11)} cdot (1-k)^{N(01)} cdot (1-k)^{N(10)}$ ,
$P( D | k )=0.5^N cdot k^{N(00)+N(11)} cdot (1-k)^{N(01)+N(10)}$ .

Обозначим количество совпадений $A=N(00)+N(11)$ , а количество несовпадений $B=N(01)+N(10)$ .

Получаем такую обобщенную формулу
$P( D | k )=0.5 ^N cdot k^{A} cdot (1-k)^{B}$ .

Желающие могу поиграться с графиком, вводя разные показатели степени:ссылка на wolframalpha.

Так как в этом примере $P( D | k )=const cdot P( k | D ) $ , то работаем напрямую с $P( D | k )$ .

Для поиска максимума дифференцируем и приравниваем к нулю:
$0=k^{A-1} cdot (1-k)^{B-1} cdot (A(k-1) + Bk)$ .

Чтобы произведение было равно нулю надо, чтобы один из членов был равен нулю.
Нас не интересуют $k=0$ и $k=1$ , так как в этих точках нет локального максимума, а третий множитель указывает на локальный максимум, поэтому
$k=frac{A}{A+B}=frac{A}{N}$ .

Получаем формулу, которую можно использовать для прогнозов. То есть после дополнительного броска первой монеты пытаемся предугадать поведение второй через $k$ .
исход 6: 1¿

При получении новых данных формулу корректируем и уточняем. При получении инсайдерских данных мы будем иметь более точное значение $P( k )$ , и можно дополнительно уточнить всю цепочку расчетов.

Так как мы вычисляем вероятность, то для $k$ желательно проанализировать среднее и дисперсию. Среднее мы как раз нашли на предыдущих шагах. А вот про дисперсию можно сказать, что при увеличении количества данных — пик на графике (ссылка выше) становится более острый, что означает более однозначный прогноз значения $k$ .

В приведенном выше наборе данных имеем 4 совпадения и одно несовпадение. Поэтому $k=4/5$ . В дополнительном шестом бросании с вероятностью 80% произойдет совпадение второй монеты с первой. Допустим мы получили на первой монете 1, тогда имеем 80%, что «исход 6» будет «11» и остальные 20%, что «исход 6» будет «10». После каждых бросков корректируем формулу и прогнозируем вероятность еще несовершенных совпадений на шаг вперед.

На этом я бы хотел закончить свой пост. Буду рад вашим комментариям.

PS
Данный пример описан для демонстрации алгоритма. Тут много чего не учтено того, что бывает в реальности. Например, при анализе событий из реального мира надо будет анализировать временные интервалы, проводить факторный анализ и многое другое. Это уже забота профессионалов. Так же следует философски отметить, что всё в этом мире взаимосвязано, только эти связи иногда проявляются, а иногда нет. Поэтому полностью абсолютно всё учесть на сто процентов не получится, ибо пришлось бы в формулу включать все объекты этого мира, даже те, которые мы не знаем, и обрабатывать очень большой объем фактического материала.

Источники информации:
1. https://ru.wikipedia.org/wiki/Теорема_Байеса.

2. https://ru.wikipedia.org/wiki/Байесовский_вывод.

3. Нейт Сильвер, «Сигнал и шум».

Рыбаков Д.А.
2017

Автор: dim2r

Источник