
Для кодов, описанных в предыдущей статье про восстановление данных, предполагалась постановка задачи, при которой минимизируется количество дисков, необходимых при операции восстановления. В [2] обсуждается применение сетевого кодирования к задачам хранения данных, получившее значительное внимание исследователей в последние годы. Здесь рассматривается не оптимизация количества дисков, необходимых для восстановления данных, а минимизация возникающего при этом сетевого трафика.
Предположим, что система хранения состоит из n узлов. Рассмотрим файл, состоящий из B символов поля GF(q), который кодируется в nα символов над GF(q) и распределяется по узлам, так, что каждый узел хранит α символов. Код построен таким образом, что данные могут быть целиком восстановлены по информации с k узлов. При этом для восстановления данных одного узла достаточно получить β ≤ α информации с d узлов [1,2], см. рис. 1. Величина γ = dβ называется диапазоном восстановления (repair bandwidth).
В [2] показано, что размер данных B ограничен сверху:
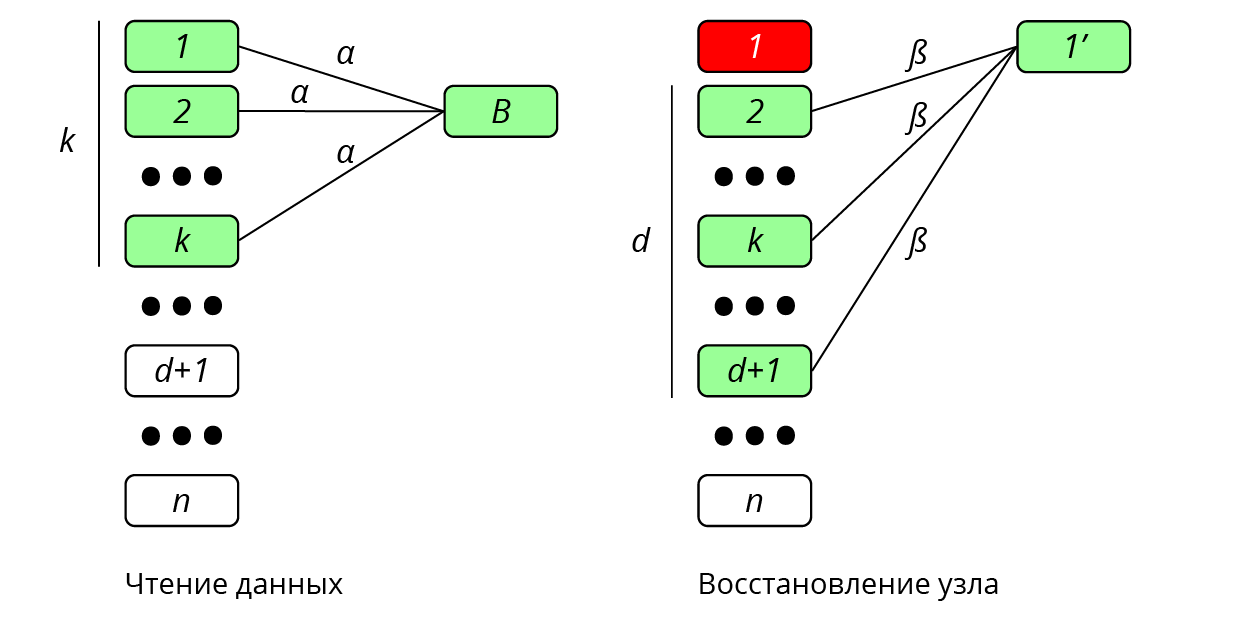
Рис 1. Регенерирующий код
Для фиксированных значений (B, k, d) существует множество пар (α, β), удовлетворяющих этой границе, что дает возможность получения компромисса относительно этих параметров, с двумя крайними точками: минимизации величины общего хранилища nα (эта точка называется «восстановлением с минимальным хранилищем», или MSR, Minimum Storage Regeneration) и минимизации диапазона γ = dβ (эта точка называется «восстановлением с минимальным диапазоном», или MBR, Minimum Bandwidth Regeneration). Коды, удовлетворяющие приведенной границе, называются регенерирующими кодами. Пример соответствующей границы приведен на рис. 2 [2].
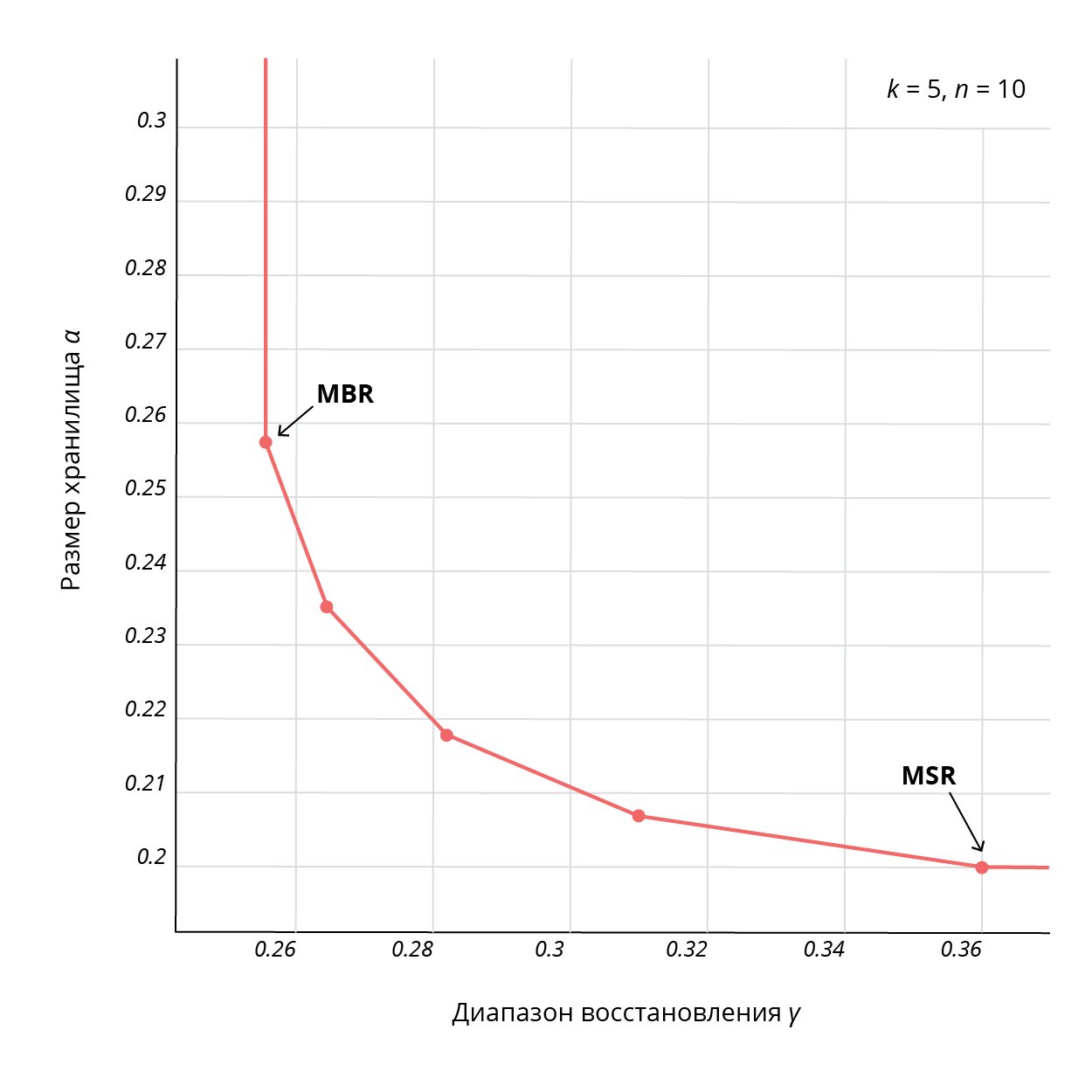
Рис. 2. Кривая MSR-MBR для регенерирующих кодов
В последние годы значительное внимание было уделено как построению кодов в точках MSR и MBR, так и кодов, лежащих на промежуточных точках границы [3,6,7]. Различные конструкции регенерирующих кодов могут быть найдены также в [8-15]. Основной недостаток этих кодов — это плохая масштабируемость.
Мы оптимизировали одну из разновидностей регенерирующих кодов — «butterfly» [4] (данный код является систематическим, это очень важно для запросов типа случайное чтение) для быстрого восстановления одного диска и улучшили масштабируемость данной конструкции.
Butterfly-схема кодирования
Рассмотрим последовательность из 

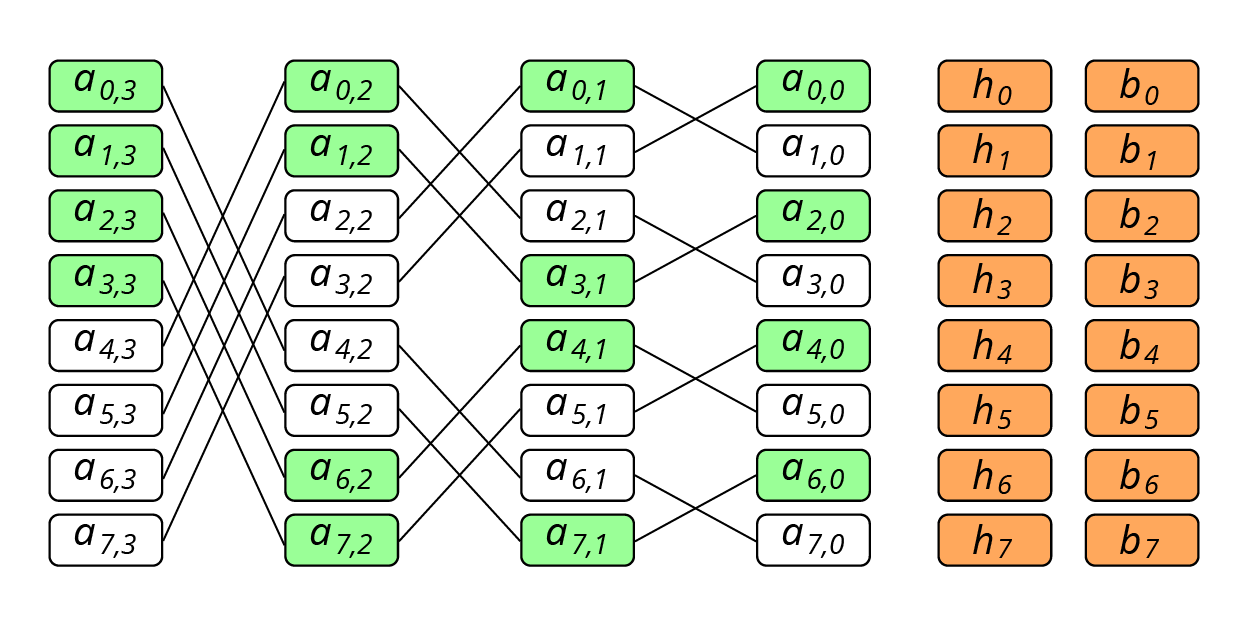
Рис. 3. Butterfly-схема кодирования
Например, расчет контрольной суммы 


В случае, если в получившемся наборе есть блоки зеленого цвета, для каждого из них необходимо включить в набор блок справа от него. Иначе говоря, если блок 


Выбор именно такого способа кодирования обосновывается в работе [4]. Так гарантируется восстановление двух одновременно отказавших компонентов.
При использовании этого способа кодирования на восстановление компонента с данными чтений потребуется меньше. А именно, для восстановления 

Однако, при отказе узла, содержащего контрольную сумму, для восстановления необходимо будет прочитать все данные, и в этом случае никакого выигрыша не будет. Эту проблему можно решить с помощью сдвига, аналогичного сдвигу в RAID-6, либо с помощью рандомизации, которую мы уже использовали в подходе с кодами локальной реконструкции. Если в каждом множестве из 
Также необходимо понимать, что регенерирующие коды имеют один существенный недостаток: строгое ограничение по количеству блоков в страйпе. Для дискового массива это несущественно, потому что размер кодируемого блока может варьироваться, а значит, может варьироваться и их количество. Но для кластерной конфигурации, в узле которой число дисков может быть ограничено, проблему масштабирования необходимо решать. Одно из возможных решений – разбиение страйпа на регенерирующие группы. Это повысит избыточность во столько раз, сколько групп будет, однако сами кодирующие множества станут экспоненциально меньше, см. рис. 4.
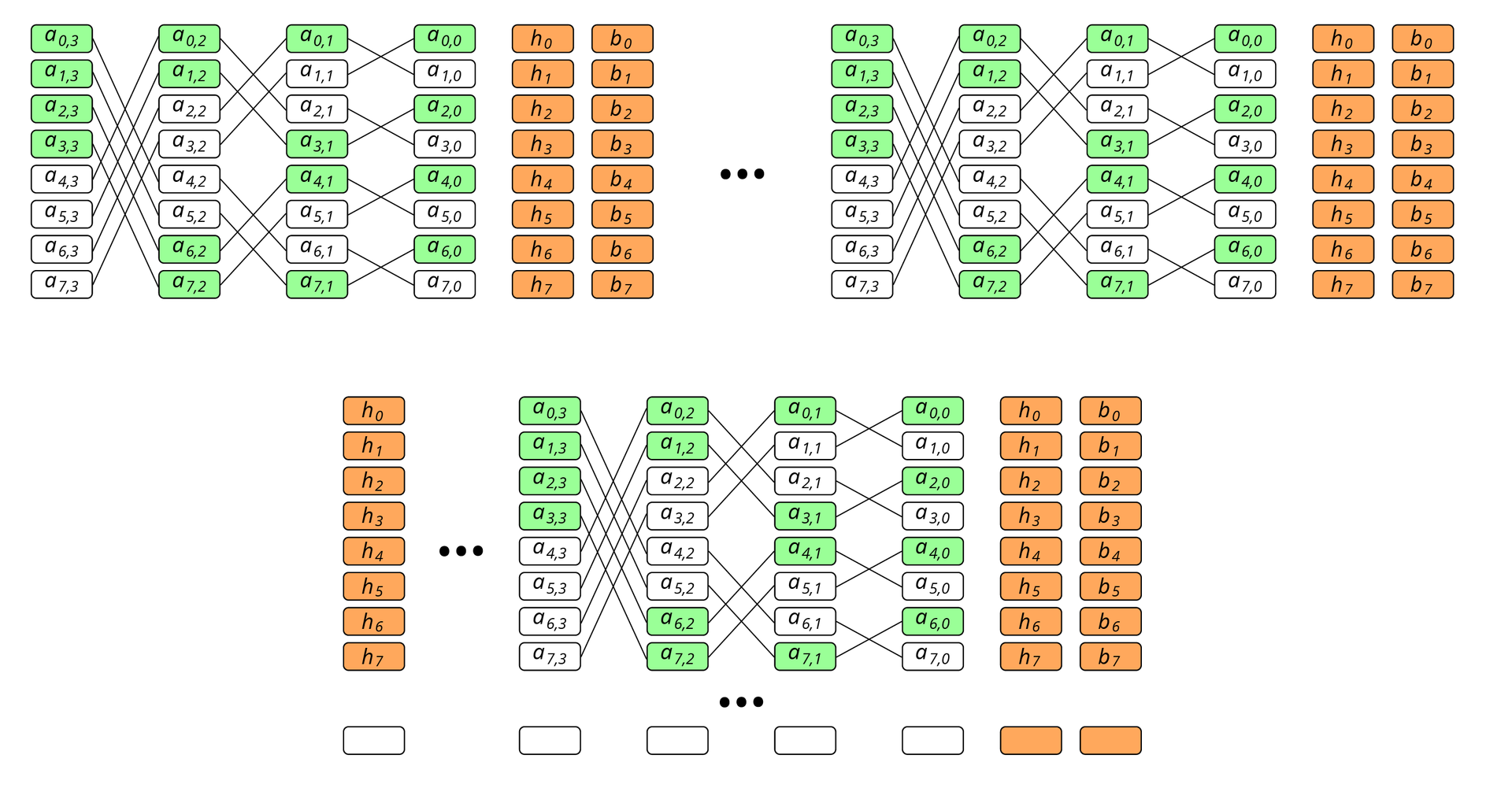
Рис. 4. Экспоненциальное уменьшение страйпов кодируемого множества
Наконец, последнее, что необходимо учитывать при применении регенерирующих кодов — это область, в которую информация с отказавшего диска будет восстанавливаться. Дело в том, что при восстановлении на hot-spare диск скорость восстановления будет ограничена скоростью записи на него, и уменьшение количества чтений не даст значимого выигрыша. Поэтому есть необходимость включить в страйп empty-блок.
Тестирование производительности
Для тестирования производительности мы создавали RAID из 22 дисков с определенными схемами размещения. RAID-устройство создавалось при помощи модификации device-mapper, которая меняла адресацию блока данных по определенному алгоритму. На RAID массив записывались данные, и для них выполнялся расчет контрольных сумм для последующего восстановления. Выбирался отказавший диск. Выполнялось восстановление данных либо на соответствующие empty blocks, либо на hot spare disk. Мы сравнили следующие схемы:
- RAID-6 — классический RAID-6 с двумя контрольными суммами, восстановление данных на hot spare disk.
- RAID-6E — RAID6 c empty блоком в конце страйпа, восстановление данных на empty blocks соответствующих страйпов.
- Classic LRC+E — LRC схема, в которой локальные группы идут последовательно и заканчиваются контрольной суммой, восстановление на empty block.
- LRC rand — для генерации каждого LRC-страйпа, его номер используется в качестве ядра генератора случайных числе, восстановление данных на empty block.
- Classic Regen — схема с тремя группами регенерирующих кодов.
- Regen rand — схема с тремя группами регенерирующих кодов и рандомизацией, восстановление данных на empty block.
Для тестирования использовались 22 диска со следующими характеристиками:
- MANUFACTURER: IBM
- PART NUMBER: ST973452SS-IBM
- CAPACITY: 73GB
- INTERFACE: SAS
- SPEED: 15K RPM
- SIZE FORM FACTOR: 2.5IN
При тестировании производительности большой эффект оказывает размер блоков страйпа. При восстановлении чтение с дисков ведется по возрастающим адресам (последовательно), но из-за декластеризации в случайных схемах расположения некоторые блоки пропускаются. Это значит, что если блоки имеют маленький размер, то позиционирование магнитной головки диска будет производиться очень часто, и это пагубно скажется на производительности. Поскольку конкретные значения скорости восстановления данных могут зависеть от модели жестких дисков, производителя, RPM, мы представили полученные результаты в относительных величинах. На рис 5. изображено то, какой прирост производительности дают схемы (b) – (f) по сравнению с классическим RAID-6.
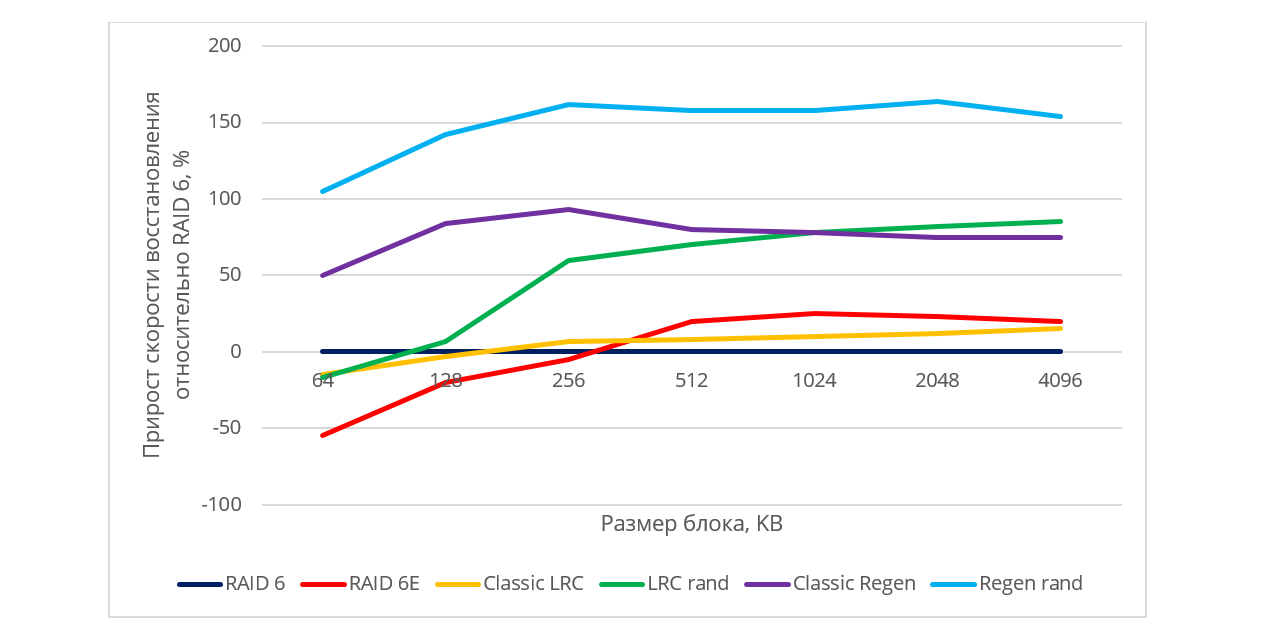
Рис. 5. Относительная производительность различных алгоритмов размещения
При восстановлении данных на hot spare диск мы получали, что скорость восстановления ограничивается скоростью записи на диск для всех схем, использующих hot spare. Можно заметить, что как рандомизированная LRC-схема, так и регенерирующие коды дают достаточно высокий прирост скорости восстановления по сравнению с не оптимальной и RAID-6. Несмотря на то, что регенерирующие коды явно лидируют по скорости восстановления, нельзя не учитывать их основные минусы: ограничение по количеству блоков в кодируемом множестве и большая избыточность: c учетом empty-блока в проверяемой конфигурации избыточность была более 30% (рис. 6).
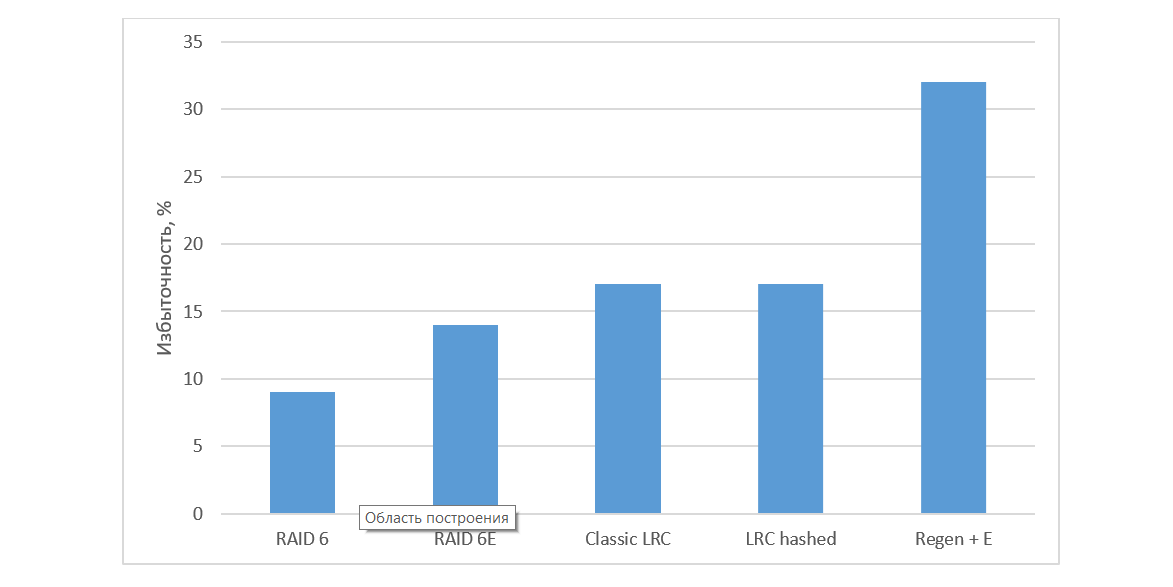
Рис. 6. Избыточность различных алгоритмов
Заключение
Регенерирующие Butterfly-коды были успешно опробованы в HDFS, Ceph[5].
Мы рассмотрели варианты применения регенерирующих кодов на локальной системе, придумали способ их масштабирования и использования для быстрой обработки ситуации отказа одного диска.
Несмотря на то, что производительность этого решения оказалась наилучшей (см. рис 5), требования по избыточности (см. рис 6) могут повлечь большие затраты, поэтому этот алгоритм подойдет не везде. Таким образом, всегда нужно понимать, можно ли в конкретном случае пожертвовать местом ради надежности.
Представленные решения могут быть обобщены на распределенную, в частности — облачную систему хранения данных. В таких системах преимущества будут еще более явными, поскольку в них узким местом является передача данных по сети, которую посредством представленных подходов можно минимизировать.
[2] A. Dimakis, P. Godfrey, Y. Wu, M. Wainwright, and K. Ramchandran. Network coding for distributed storage systems. Information Theory, IEEE Transactions on, 56(9):4539–4551, Sept 2010.
[3] T. Ernvall. Exact-regenerating codes between mbr and msr points. In Information Theory Workshop (ITW), 2013 IEEE, pages 1–5, Sept 2013.
[4] E. En Gad, R. Mateescu, F. Blagojevic, C. Guyot, and Z. Bandic. Repair-Optimal MDS Array Codes Over GF (2). In Information Theory Proceedings (ISIT), IEEE International Symposium on, 2013.
[5] Lluis Pamies-Juarez, Filip Blagojević, Robert Mateescu, Cyril Guyot, Eyal En Gad, Zvonimir Bandic. Opening the Chrysalis: On the Real Repair Performance of MSR Codes. In Proceedings of the 14th USENIX Conference on File and Storage Technologies (FAST ’16), pages 81-94. USENIX Association, 2016.
[6] J. Li, T. Li, and J. Ren. Beyond the mds bound in distributed cloud storage. In INFOCOM, 2014 Proceedings IEEE, pages 307–315, April 2014.
[7] N. Shah, K. V. Rashmi, P. Kumar, and K. Ramchandran. Distributed storage codes with repair-by-transfer and nonachievability of interior points on the storage-bandwidth tradeoff. Information Theory, IEEE Transactions on, 58(3):1837–1852, March 2012.
[8] J. Chen and K. Shum. Repairing multiple failures in the suhramchandran regenerating codes. In Information Theory Proceedings (ISIT), 2013 IEEE International Symposium on, pages 1441–1445, July 2013.
[9] B. Gaston, J. Pujol, and M. Villanueva. Quasi-cyclic regenerating codes. CoRR, abs/1209.3977, 2012.
[10] S. Jiekak, A.-M. Kermarrec, N. Le Scouarnec, G. Straub, and A. Van Kempen. Regenerating codes: A system perspective. In Reliable Distributed Systems (SRDS), 2012 IEEE 31st Symposium on, pages 436– 441, Oct 2012.
[11] K. V. Rashmi, N. Shah, and P. Kumar. Optimal exact-regenerating codes for distributed storage at the msr and mbr points via a productmatrix construction. Information Theory, IEEE Transactions on, 57(8):5227–5239, Aug 2011.
[12] K. Shum and Y. Hu. Exact minimum-repair-bandwidth cooperative regenerating codes for distributed storage systems. In Information Theory Proceedings (ISIT), 2011 IEEE International Symposium on, pages 1442–1446, July 2011.
[13] K. Shum and Y. Hu. Functional-repair-by-transfer regenerating codes. In Information Theory Proceedings (ISIT), 2012 IEEE International Symposium on, pages 1192–1196, July 2012.
[14] K. W. Shum and Y. Hu. Cooperative regenerating codes. CoRR, abs/1207.6762, 2012.
[15] C. Suh and K. Ramchandran. Exact-repair mds code construction using interference alignment. Information Theory, IEEE Transactions on, 57(3):1425–1442, March 2011.
Автор: raidixteam










