Задача: Найти функцию для графика (бесконечного в обе стороны оси ОХ):
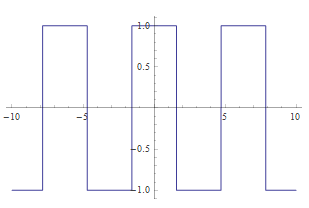
Ограничения: Должны использоваться только тригонометрические функции (любые прямые и обратные) и знаки операций плюс, минус, разделить, умножить, модуль. Решение должно быть представлено одной формулой.
Подсказка: Раздумывая над этой задачей, мне попалось на глаза видео о так называемой квантовой запутанности фотонов. Я подумал, что фотон все же в большей мере волна, чем частица, поскольку частицей он определяется при определенных условиях, связанных с измерением состояния фотона, в остальных случаях — это волна. А где волна там обязательно должны быть тригонометрические функции косинуса и синуса, как минимум. Поэтому я подумал, что скорей всего вполне возможно, что есть вероятность создать «запутанную пару» от аргумента x для какой-то неизвестной функции с использованием только тригонометрических функций. Как ни странно, но именно поиск этой неизвестной функции, привел меня к решению поставленной выше задачи.
Как смоделировать запутанность? У нас есть прямые и обратные тригонометрические функции, есть переменная x-фотон и несколько тривиальных операций. Первое что приходит на ум (по крайне мере мне) это рассмотреть графики функций ArcSin[Cos[x]] и ArcCos[Sin[x]]:
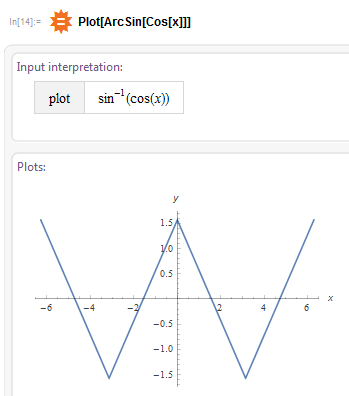
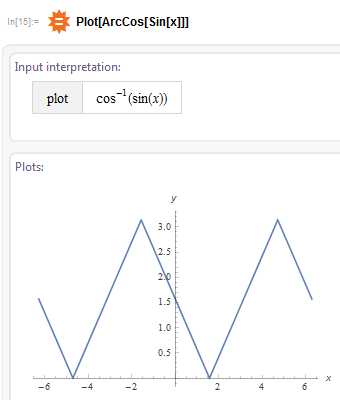
Приведенные графики уже очень напоминают нужный нам «квадратичный косинус», но чего-то не хватает, оказывается не хватает «запутанности», то что мы сделали — это по сути запутанность первого уровня, но этого не достаточно, нужно эти две функции как-то скомпоновать, выйдя на запутанность второго уровня. После нескольких экспериментов с доступными тривиальными операциями я остановился на делении и вот что получилось (рис. 4):
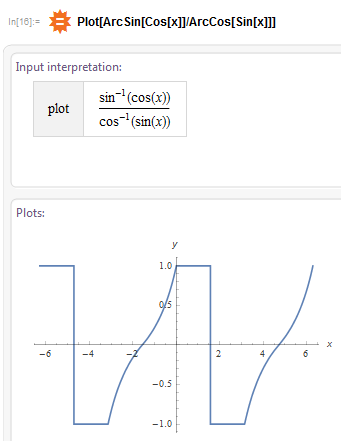
Именно здесь я понял, что не потерялся в запутанности x-фотона и все как раз проясняется.
Казалось бы, наполовину задача решена и остается тупо скопировать решение в две формулы вида:
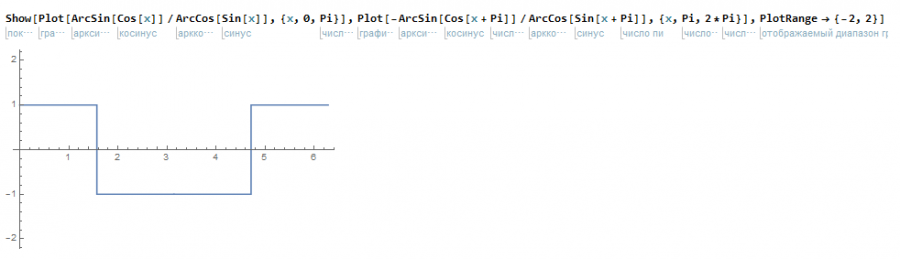
Но мне хотелось всё представить одно формулой и поиски продолжились…
Поэтому пришлось анализировать график, представленный на рис.4. Что в нем примечательного?
Во-первых, наполовину квадратичность присутствует, но нужно избавиться от этих восходящих линий. Как этого добиться? Только «аннигиляцией», то есть самоуничтожением противоположностей. И как раз здесь нам и понадобится модуль, чтобы у нас были симметричные плавно восходящие и нисходящии линии. Поэтому я рассмотрел такой график:
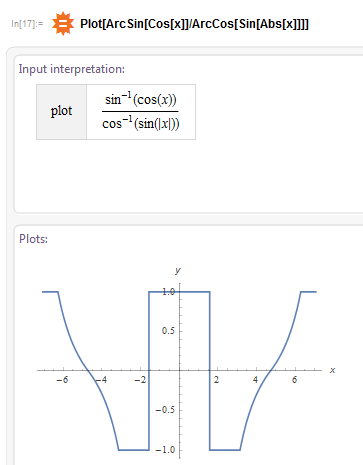
Казалось бы, маленькое отличие — модуль, но большая разница — теперь мы имеем симметричные (относительно начала координат) восходящие и нисходящии линии, которые достаточно «сложить» и они превратятся в квадрат… Но складывать их не нужно, достаточно еще одного модуля уровнем выше:
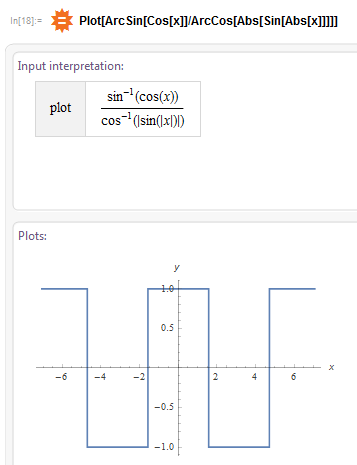
Что и требовалось доказать.
Эту функцию
y=ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]]я назвал "белая функция", поскольку она настолько же идеальна и гармонична, как и белый цвет. Белая функция представляет собой сложную функцию-модель квантово-запутанной саму с собой пару от аргумента x. Белая функция к тому же определяет собой целый класс одноименных тригонометрических функций вида
y=ArcSin[f1[x]]/ArcCos[Abs[f2[x]]], например, к этому виду можно также отнести функцию
y=ArcSin[1/Tan[x]]/ArcCos[Abs[Tan[x]]]и т.д.
Исходники в формате Wolfram Mathematica — yadi.sk/d/3pl0lZMH3PzxCU
Evaluate[Integrate[
ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]], {x,
N[Pi, 100]/2 - 0.000000000000000000001`100, N[Pi, 100]/2}]]

Здесь я думаю меня сочтут полным профаном, но я всё таки скажу, что это означает.
Очевидно по результату в пределе действительная часть стремится к бесконечность, а мнимая к нулю то есть ∞+0.0*i
Что это может означать? Какой смысл в действительной части и мнимой? Я думаю, что действительная часть пропорциональна точности
(в чем легко убедиться увеличивая количество нулей в формуле выше для приближения к точке Pi/2), а мнимая часть пропорциональна погрешности вычисления и эта погрешность стремиться к нулю в пределе.
Посему заключаем, что найденная формула белой функции делает возможным расчет с управляемой точностью, что не может не радовать. Но как такое возможно? Ответа у меня нет — думайте своей головой.
Очевидно, эти способы не идут не в какое сравнение с найденным решением по точности и производительности, нет необходимости в сложении сотен косинусов, как это делает ряд Фурье.
Моделирование форм с помощью найденной функции
Тривиальный пример, куб:
a[x_] := ArcSin[Cos[x]]/ArcCos[Abs[Sin[x]]]; (*белая функция*)
b[y_] := ArcSin[Cos[y]]/ArcCos[Abs[Sin[y]]]; (*белая функция*)
c[z_] := ArcSin[Cos[z]]/ArcCos[Abs[Sin[z]]]; (*белая функция*)
f[x_, y_] := a[x]*b[y];
time[t_] := c[t];
z = Table[
Plot3D[10*move*(1 + f[x, y]*time[move]), {x, -3*Pi/2,
3*Pi/2}, {y, -3*Pi/2, 3*Pi/2},
PlotRange -> {-50, 50}], {move, -Pi/2 + 0.1, Pi/2 - 0.1, Pi/100}];
z = Join[z, Reverse[z]];
Export["C:\out.gif", z,
"AnimationRepetitions" -> Infinity]
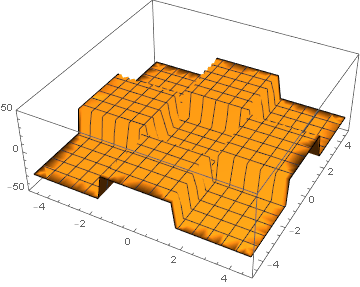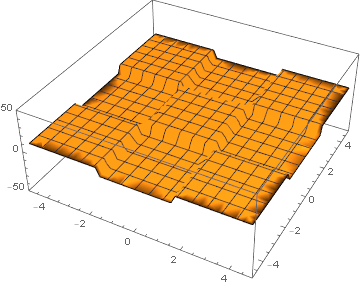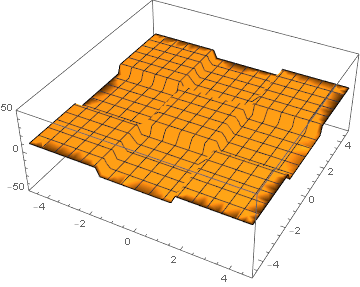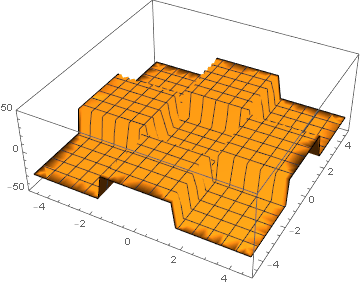
Автор: Алексей


