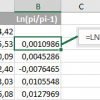
Проблематика вопроса сформулирована в предыдущей статье.
А именно: как оценить влияние определенного допущения модели Блэка-Шоулза на расчетную величину премии по европейскому опциону? Допущения о том, что цена торгуемого актива имеет логнормальное распределение. Как альтернативу расчета по формуле Блэка-Шоулза я использовал подход — прогнозирование выплат покупателю опциона методом Монте-Карло. На вход программе я подавал:
- “эталонные данные” (моделирование логнормального распределения”),
- случайный ряд, характеризующийся распределением с “толстыми хвостами”,
- и, наконец, цены нескольких биржевых активов — валютных пар и криптовалют.
В каждом случае я рассчитал премию опциона по формуле Б-Ш и методом Монте-Карло. Сравнил результаты и сделал(?) выводы:

Ранее я построил в MS Excel два гипотетических ценовых ряда: ABS/USD — ценовой ряд, описываемый логнормальным законом распределения. И серию WRD/USD — ценовой ряд, распределение которого характеризуется большей вероятностью меньших изменений при существенной вероятности больших (> 3σ) изменений.
Коэффициенты в таблице Excel были подобраны так, чтобы оба этих виртуальных ценовых активов характеризовались одинаковой величиной HV. При таких условиях и равных параметрах опционного контракта (текущая цена, страйк, экспирация) расчет премии по опциону ABS/USD и WRD/USD по формуле Блэка-Шоулза даст одно и то же значение для обоих активов.
Альтернативный способ оценить размер премии — моделировать выплаты по опциону методом Монте-Карло. Провести ряд итераций, на каждой итерации моделируя цену на N дней вперед. В конце итерации посчитать прибыль покупателя опциона.
“Справедливая” премия по опционному контракту будет нами получена, как сумма выплат, деленная на количество итераций. Вопрос: совпадет ли премия, рассчитанная таким способом (программно) с премией, рассчитанной по формуле Б-Ш?
Ну и, наконец, я собираюсь применить ту же методику оценки премии для исторических данных реальных биржевых активов. Нескольких валют и криптовалют, торгуемых за другие валюты и криптовалюты.
В следующей таблице я рассчитал цену WRD/USD (распределение цены имеет “толстые хвосты”) несколько раз подряд на 30 дней вперед. Как и прежде, цена WRD/USD изменялась каждый день в 
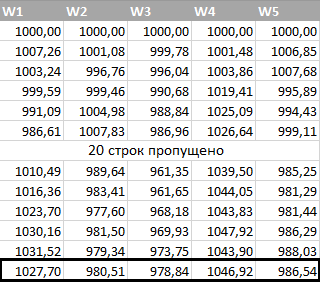
В 2-х случаях из 5 цена актива WRD/USD выросла, в 3-х случаях — упала:
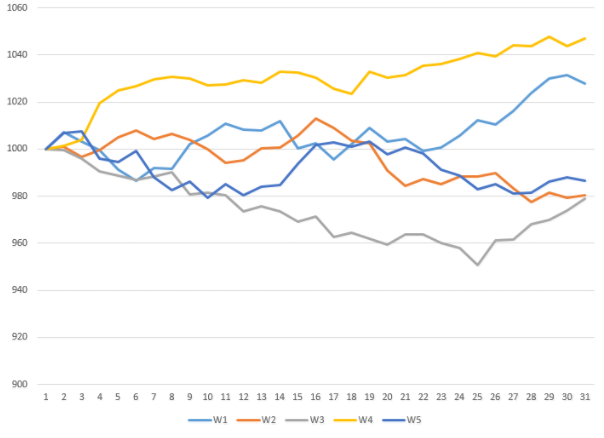
Соответственно, в 2-х случаях покупатель CALL-опциона смог реализовать прибыль, равную
(1027.70 — 1000) + (1046.92 — 1000) = $74.62.
Делим $74.62 на количество возможных исходов (5) и получаем премию, что составит $14.92. Несколько больше, чем дал нам предыдущий расчет методом Б-Ш. Но так и метод наш не очень точен: всего 5 итераций.
Программное моделирование покупки опциона
На этом этапе Excel нам уже недостаточно. Я провел 5 имитационных экспериментов: заполнил 5 столбцов сгенерированной для нашего гипотетического актива WRD/USD ценой. Но для нашей цели — хорошей сходимости оценки премии по опциону — не хватит и 500 экспериментов.
Кроме того, как мы помним, цена WRD/USD — функция от СВ с функцией плотности — суммой функций плотности двух нормальных распределений. Случайная последовательность, подчиняющаяся закону распределения, измысленному мной в качестве примера. С параметрами, подобранными исключительно в целях демонстрации, но не отражающими динамику цен какого-либо реального товара. Это совсем не то, что нам потребуется для анализа биржевого актива. Нам нужна программа, реализующая логику вида:
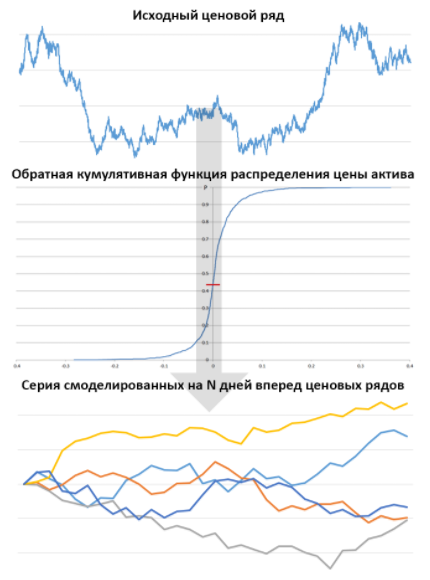
Логика программы на высоком уровне:
- 1) прочитать из источника (файла) исходный ценовой ряд
- 2) провести предварительную обработку ценовых данных
- 3) построить таблицу кумулятивной функции распределения исходного ценового ряда
- 4) используя таблицу, полученную на шаге выше, и генератор равномерно распределенной СВ, провести N экспериментов:
- 4.1) в каждом эксперименте рассчитать M последовательных (автокоррелированных) цен
- 4.2) вычислить прибыль покупателя опциона — разность последней цены и страйк цены. Для Put-опциона разность берется с обратным знаком
- 5) сложить прибыль покупателя, полученную на каждом из N шагов и поделить результат на N
Устранение тренда
В простом алгоритме, приведенном выше, один пункт требует объяснений: “предварительная обработка ценовых данных”. Поясню на примере графика цены актива ABS/USD (распределение цены — логнормальное), полученного нами ранее:
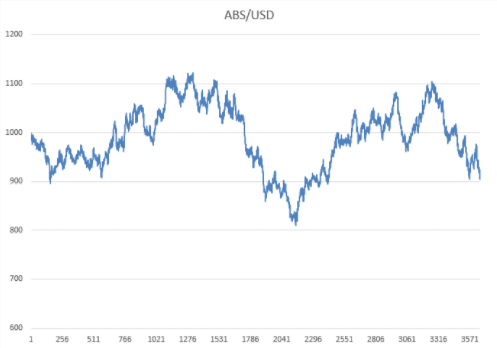
конечная цена актива ABS/USD ниже исходной цены. Нисходящий тренд нашего актива — не закономерность, но влияние недетерминированного фактора — напомню, мы использовали генератор случайных чисел.
В то же время, про актив ABS/USD априори известно, что его цена, в общем случае, дрейфует равновероятно вверх либо вниз. То есть, в модели математическое ожидание отклонения цены ABS/USD равно 0.
В статистической оценке математическое ожидание — среднее значение ценового изменения — получилось отрицательным.
Корректно ли использовать для расчетов данные, в которые уже заложено априорное “знание” об отрицательной доходности актива? Слово “знание” неспроста забрано в кавычки: мы знаем, что актив ABS/USD имеет равную вероятность как вырасти в цене, так и подешеветь. Такова модель данных, использованная нами в расчете.
С другой стороны, статистика показывает нам отрицательное математическое ожидание дневной ценовой динамики. И это “знание”, полученное на, по сути, случайной, выборке, мы заложим в модель.
ABS/USD — актив гипотетический. Совершенно определенно можно сказать, что, для построения таблицы — функции распределения, что впоследствии будет использована для генерации ценовых прогнозов, имеющийся тренд — статистическая ошибка, которую необходимо устранить.
Но что если мы анализируем реальный рыночный актив? Не ABS/USD, а, например, EUR/USD? Как быть с трендом, имевшим место в действительности?
Мое мнение: из истории цен тренд необходимо убрать. Обратное справедливо, если у нас есть «достоверные» данные о том, что цена актива продолжит снижение в будущем. Да, есть такие валюты, товары и прочие объекты торговли, на динамику ценообразования которых экономический анализ дает определенный прогноз. Чего нельзя сказать, например, о большинстве криптовалют.
Там, где достаточно аргументированных высказываний как в пользу восходящего, так и в пользу нисходящего тренда, исторические цены должны быть “выровнены”:
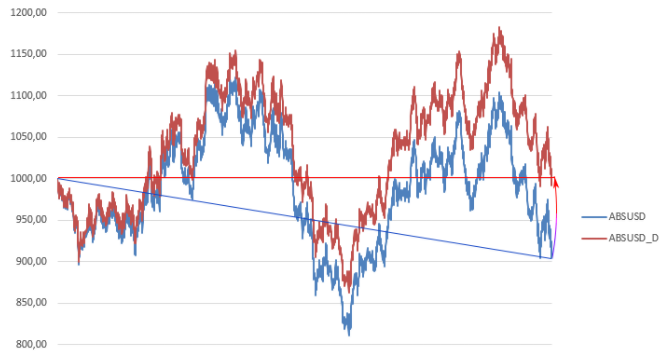
На рисунке исходная синяя кривая была скорректирована: из каждого i-го значения цены вычтена величина, равная i*d, где d равна разнице первой и последних цен, деленной на количество временных отрезков (количество цен минус 1).
В прикладной программе, предназначенной для оценки величины премии по опционному контракту, вероятно стоит предусмотреть два варианта расчета: с устранением тренда и с данными, взятыми и использованными, как есть.
Определенно, там, где у нас нет полной уверенности в динамике цен на прогнозируемый период, тренд следует устранить. А если уверенность есть — стоит ли тратить время на изучение деривативов, когда можно просто выйти на рынок со всеми доступными средствами, и, с ощутимой выгодой, монетизировать свои прогнозы?
Еще замечание: тренд необязательно устранять непосредственно из цен. К примеру, биткойн с его ростом более чем на сто процентов за один только год после удаления из цен трендовой составляющей вообще зайдет в отрицательную полуплоскость по оси цены. Отрицательная цена, определенно, не годится для дальнейших расчетов. Альтернатива, которой я и воспользуюсь — удалить тренд из ряда ценовых изменений — 

Построение и использование обратной кумулятивной функции распределения
В программе, что я приведу в депозитарии кода github по ссылке, пожалуй, самая “интеллектуальная” часть — это построение обратной кумулятивной (интегральной) функции распределения и использования ее для генерации случайного ценового приращения. Весь процесс разбит на несколько шагов.
На первом шаге я получаю из цен 
Далее, если выбрана опция устранения тренда, я получаю новый ряд приращений цен, вычитая из каждого значения 

Значения приращений цены я сортирую по возрастанию.
Процесс построения обратной функции распределения реализован в одном цикле. Представим, что цена изменяется (








Т.е., имея отсортированный ряд 
.
Итак, обратная функция построена. Как нам получить “случайное” значение изменения цены, используя таблицу и генератор равномерно распределенных случайных чисел?
Примерно так же, как мы это делали в Excel.
К примеру, моя таблица содержит 500 записей вида:
| Вероятность, P | Дельта, D |
| 0.002 | -0.0172 |
| 0.004 | -0.0699 |
| ... | ... |
В построенной программой таблице 1-я записи соответствует вероятность, равная 1 / 500, второй — 2 / 500 и так далее.
Я получаю случайное дробное число в диапазоне от 0 до 1. К примеру, 0.269.
Умножаю случайное число на количество записей в таблице (500): 0.269 * 500 = 134.5.
Нужное мне значение дельты будет “посередине” между 134-й и 135-й строкой таблицы:
Как только мы интерполировали значение приращения цены, мы вычисляем новое значение цены по формуле
Результаты моделирования
Сейчас моя задача — верифицировать алгоритм расчета премии по опциону с использованием алгоритма, описанного выше. Верифицировать на примере расчета, проведенного для активов ABSUSD (логнормальный) и WRDUSD (толстохвостый). Напомню: ABSUSD характеризуется приращениями цен, имеющими логнормальное распределение. То самое распределение, что предполагает модель Б-Ш. Актив WRDUSD демонстрирует динамику цен, более близкую к реальному рынку.
В программе я указал ровно те же параметры, что и для расчетов в Excel. Вместо вычисления премии по формуле, использующей стандартное отклонение, на вход программе я передал ценовые временные ряды наших активов. Результат демонстрирует таблица:
| - | ABS/USD | WRD/USD |
| закон распределения цен | логнормальное распределение | “реальное” распределение |
| премия по формуле Б-Ш | 10.80 | 10.80 |
| премия, полученная в результате моделирования динамики цен | 10.70 | 11.20 |
расчет для актива ABS/USD дает практически тот же результат, что и формула Б-Ш. А вот для актива WRD/USD “моделированная” премия уже заметно отличается от результата аналитического расчета.
Причин тому может быть две: сама природа ценового ряда WRD/USD и / или ошибка выборки.
Мы должны быть уверены, что различие в результатах моделирования и аналитического расчета обусловлено именно природой нашего виртуального актива. С этой целью я проведу 10 итераций расчета премии, сгенерировав 10 рядов цен WRD/USD. Для каждой такой выборки посчитаю стандартное отклонение, подставлю его в формулу Б-Ш и получу результат аналитического расчета:
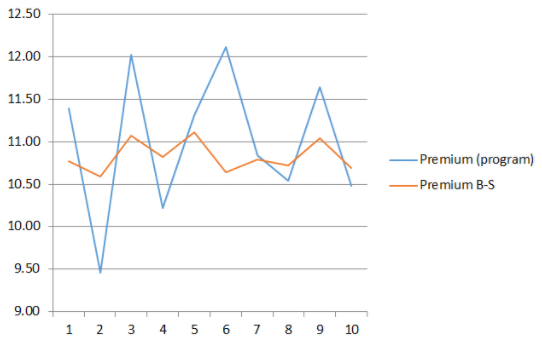
Можно сказать, что ошибка выборки в большей степени повлияла на результат расчета программы, чем на результат вычислений по формуле Б-Ш. В ходе 10 экспериментов были получены средние значения размера премии:
- программный результат: 11.0,
- по формуле Б-Ш: 10.83.
Различия в результате незначительны. Из чего можно сделать вывод: до сих пор значительного влияния закона распределения цен на оценочное значение “справедливой” премии по опционному контракту мне обнаружить не удалось.
Расчет премии по рыночным контрактам
До сих пор мы анализировали “виртуальные” активы, динамика которых подчиняется законам, нами же и сформулированными. Цель же настоящих изысканий — оценить реальные активы. Опционные контракты на криптовалюты, стоимость которых выражена в фиатных валютах либо других криптовалютах.
Как и раньше, возьмем ванильный 30-дневный опцион BTCUSD — курс Bitcoin к доллару США. Проведем 4 итерации расчета. Для первой итерации в качестве входных данных возьмем всю историю котирования BTCUSD, с 2011 по 2017 год. Посчитаем премию, устранив тренд из исходных данных. Текущей ценой примем $10 709 за 1 биткойн.
Премия, полученная аналитически (Б-Ш), составила $1234.
Моделированием ценового ряда в программе получаем величину премии $1938.
Расхождение аналитического результата с программным в случае BTCUSD на сей раз значительное.
В качестве исходных данных мы взяли всю историю котирования биткойна. Вообще, при расчете премии по опциону принято брать не все имеющиеся данные, но относительно “свежую” историю цен. Тот же биткойн прошел через череду взлетов и обвалов цен, характерную для развивающегося, “незрелого” рынка.
Очевидно, было бы странно строить оценку стоимости опциона сегодняшнего популярного и ликвидного актива, отталкиваясь от истории 7-летней давности, когда биткойн был диковинкой, а капитализация его была ничтожна.
Биткойн образца 2011 года и биткойн нынешний, с точки зрения финансового мира — два разных актива. Потому я повторю расчеты, ограничившись периодом 2014 — 2017 гг, затем периодом 2016 — 2017 год:
| - | HV, % | Премия (программа) | Премия (Б-Ш) |
| 2011-2017 | 101.15 | 1938.34 | 1234.67 |
| 2014-2017 | 66.26 | 1127.22 | 810.40 |
| 2016-2017 | 62.96 | 1407.93 | 770.15 |
Чему можно приписать такое значительное расхождение премии, рассчитанной двумя способами? Ошибке выборки или же плохой применимости формулы Б-Ш для волатильного, “непредсказуемого” криптоактива?
Для сравнения, приведу данные по расчету премии опционов на популярные валютные пары / золото:
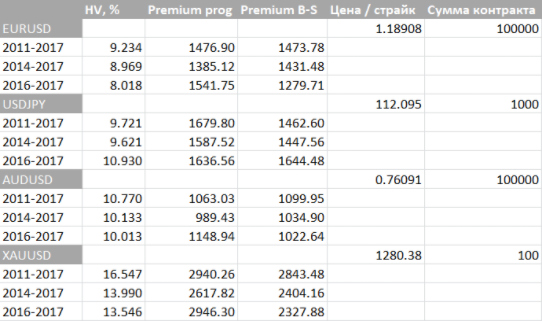
Для “зрелых” рынков, как видно из таблицы, расхождения в результатах моделирования с формулой Б-Ш не столь значительны, как для BTCUSD (биткойна).
Следующая диаграмма показывает, как различаются рассчитанные значения премии (программа / формула Б-Ш) для фиатных валют, золота и криптовалют:
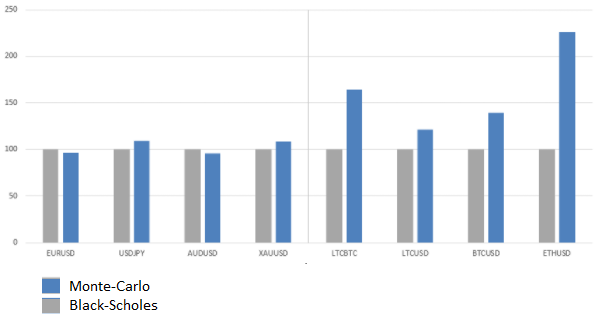
Рекомендации к практической оценке премии опционного контракта
При расчете опционной премии актива столь непредсказуемого и динамичного, как криптовалюта, стоит учесть ряд факторов.
Во-первых, можно предположить сильное влияние ошибки выборки на расчет премии. Это предположение, очевидно, подтверждает эксперимент с десятью выборками искусственного временного ряда WRDUSD.
Во-вторых, оценка “справедливой” премии, полученная программным моделированием на разных интервалах истории цен актива, может значительно отличаться от оценки, рассчитанной по формуле Б-Ш от исторической волатильности. Персонально я отдаю предпочтение более консервативной, пусть, вероятно, завышенной, оценке, полученной моделированием ценового ряда.
В третьих, один и тот же актив в разные периоды может характеризоваться разной динамикой. Вообще говоря, существует более общая относительно модели Б-Ш модель ценовой динамики — модель Хестона, предполагающая “дрейфующую” волатильность актива. В случае криптовалютных активов модель Хестона, вероятно, будет избыточно сложна и не вполне адекватна (при определенных условиях). Вместо предположения о стохастической, стремящейся вернуться к среднему значению волатильности, логичней предположить, что волатильность цен криптовалют меняется со временем, “эволюционирует”, обратно коррелируя с ростом капитализации рынка.
Наконец, в своей оценке я предполагаю свою полную неосведомленность относительно формирующегося ценового тренда. Оценка премии по “ванильному” CALL опциону, полученная без устранения тренда, будет превышать оценку премии опциона PUT на 40% — 70%. Даже если я приму решение оставить тренд в исторических данных, сценарий роста криптоактива — лишь один из возможных сценариев. Выбирая из двух альтернатив, я, например, могу остановиться на “взвешенном” значении премии:
,
где
- C — премия (неважно, по опциону call или put),
— премия, рассчитанная по данным, в которых тренд сохранен,
— премия, рассчитанная по данным после удаления тренда,
— моя оценка вероятности сохранения имеющегося тренда.
И последний в списке, но первый по значимости принцип, которым я руководствуясь: говоря о “справедливой” премии по опциону я забираю слово “справедливой” в кавычки. Говоря о рассчитанной по истории наблюдений вероятности я говорю не о вероятности как таковой, а о ее оценке. Строгость формулировок помогает мне хоть сколько-нибудь сохранять критическое отношение к собственным (а к чужим — и подавно) прогнозам и допущениям.
Автор: AndreySitaev



![Расчет премии по опциону методом Монте-Карло vs формула Блэка-Шоулза - 24 $[d_1, frac{1}{N-1}], [d_2, frac{2}{N-1}], … [d_{N-1}, frac{N-1}{N-1}]$](https://www.pvsm.ru/images/2017/12/23/raschet-premii-po-opcionu-metodom-monte-karlo-vs-formula-bleka-shoulza-24.svg)