Мозаика в ванной и диофантовы уравнения

Дело было вечером, перед сном. Чистил я зубы и устало разглядывал мозаику в ванной. Почему-то меня заинтересовал такой простой факт: если прямоугольник из клеточек 2×3 обвести с двух сторон ещё клеточками, то площадь обводки окажется такой же как площадь прямоугольника:

Мозаика в ванной и диофантовы уравнения - 1

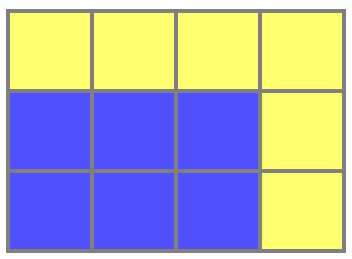
Голубых квадратиков ровно столько, сколько жёлтых. И тут меня понесло.

Я задумался, а бывают ли ещё подобные конфигурации. То есть чтобы прямоугольник $a times b$ обвести контуром с двух сторон, и площадь контура совпадала с площадью прямоугольника. Разумеется, $a$ и $b$ должны быть целыми:

Мозаика в ванной и диофантовы уравнения - 5

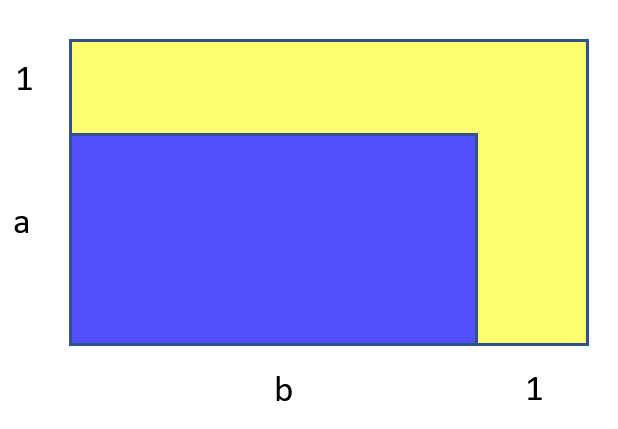
Кажется, таких случаев больше быть не должно. Площадь голубой части $a times b$ , а жёлтой — $a + b + 1$ . Видно, что если $a$ или $b$ единица, то совпадений не будет, а если увеличивать их больше $2 times 3$ , то голубая будет явно расти быстрее. Так что такая конфигурация одна.

Скучно, сказал мозг ^[1]. Надо ослабить задачу. Скажем, так:

Мозаика в ванной и диофантовы уравнения - 11

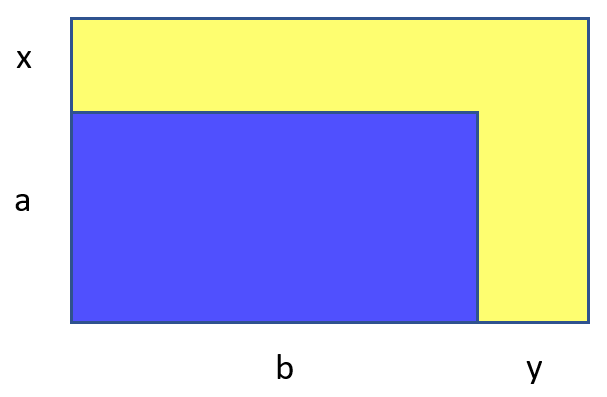
Но теперь задача слишком ослабла. По сути надо подобрать два прямоугольника с целочисленными сторонами, так что их площади отличаются ровно вдвое. И на прямоугольники ограничение только в том, чтобы один можно было засунуть в другой. Таких слишком много, тоже скучно. Давайте так:

Мозаика в ванной и диофантовы уравнения - 12

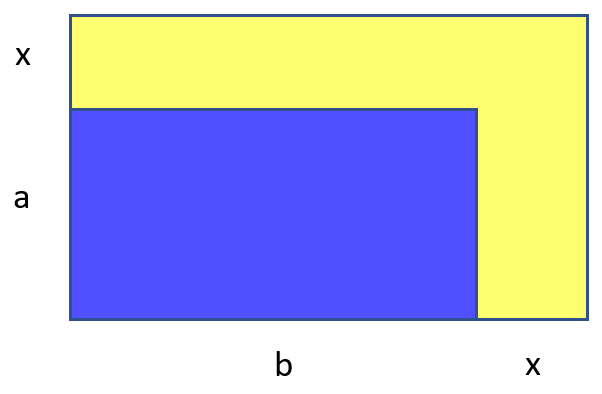
Зафиксируем ширину окантовки. Много ли таких найдётся? Хм. Выглядит интереснее. Жёлтая площадь — это $(x + a)(x + b) - ab$ , и нам хочется, чтобы она равнялась просто $ab$ . То есть нам (мне и моему мозгу ^[1], который меня в это втянул) надо решить уравнение:

$(x + a)(x + b) - ab=ab$

Или, что то же самое:

$x^2 + ax + bx - ab=0$

К этому времени я закончил с зубами и принялся насыпать порошок в посудомойку. Ага, сказал мозг ^[1], неплохой челлендж. Решить надо, конечно, в целых числах, то есть это диофантово уравнение ^[2]. Диофантовы уравнения мы в универе не проходили, но я вспомнил кое-что о них из популярных статей. А именно:

Если у нас однородное уравнение, то нам повезло.
Однородное уравнение на целых числах легко превратить в уравнение на рациональных, уменьшив число переменных на одну.
Если методом пристального вглядывания найти какой-нибудь корень квадратного уравнения на рациональных числах, то несложно найти все остальные.
Любая прямая с рациональными коэффициентами, проходящая через известный корень, пройдёт через ещё один корень. Крутя эту прямую, можно получить все рациональные корни.

Таким способом легко находится, например, общая формула для всех пифагоровых троек ^[3]. Кстати, как и с пифагоровыми тройками, в нашей задаче любое количество кратных решений. Например, прямоугольник $4 times 6$ можно расширить окантовкой в два квадратика и так далее. Разумеется, нам интересны только некратные решения.

Смогу ли я проделать всё это в уме, подумал я, набирая увлажнитель. Алгебра без бумажки и компьютера — довольно коварная штука: перепутал плюс с минусом или забыл какой-нибудь член, и дальнейшие вычисления насмарку. Программисты знают, что делать, чтобы снизить вероятность ошибки — надо обложиться юнит-тестами. К счастью, мы знаем уже одно решение: $x=1; a=2; b=3$ . Будем на каждом шагу его проверять.

$1^2 + 2 times 1 + 3 times 1 - 2 times 3=0$

Пока всё идёт хорошо. Итак, у нас однородное уравнение — все члены входят во второй степени. Поделим уравнение на $x^2$ (случай $x=0$ нас не интересует, значит, делить можно):

$1 + frac a x + frac b x - frac a x times frac b x=0$

Делаем замену: $p=a / x; q=b / x$ и получаем уравнение с двумя рациональными переменными:

$1 + p + q - pq=0$

В нашем юнит-тесте $p=2; q=3$ , тест проходит. Теперь надо проводить прямую. В принципе её можно проводить как раз через точку $(2; 3)$ , но в мозгу ^[1] это сложно держать. Зато методом пристального вглядывания мы легко можем найти другую точку, которая удовлетворяет уравнению: $p=-1; q=0$ . Это соответствует нулевой площади $a times b$ и опять же как решение не очень интересно, но для проведения прямой в самый раз. Довольно просто заметить, что все прямые (кроме одной), проходящие через $p=-1; q=0$ , описываются явным уравнением $q=alpha(p+1)$ (да, почему-то мозг ^[1] выдал греческую букву, хотя и латинские ещё не кончились). Одна недостающая прямая — это $p=-1$ , она тоже не очень интересна нам. Разумеется, любой рациональной точке $(p; q)$ , где $p neq -1$ соответствует рациональная $alpha$ . Например, для точки $(2; 3)$ значение $alpha=1$ . Подставим уравнение прямой в наше уравнение и получим:

$1 + p + alpha(p+1) - alpha p(p+1)=0$

Или

$1 + p + alpha p + alpha - alpha p^2 - alpha p=0$

Или

$1 + p + alpha - alpha p^2=0$

Или

$alpha p^2 - p - (1 + alpha)=0$

В голове становится сложно приводить члены, мозг ^[1] отчаянно просит бумажку. Но я убаюкиваю на руках младенца, тут уж не до бумажки. Прогоним юнит-тест ( $p=2; alpha=1$ ):

$1 times 2^2 - 2 - (1 + 1)=0$

Фуф, пока всё хорошо. Теперь у нас есть квадратное уравнение относительно $p$ , которое вообще-то должно выдать рациональный корень для любого рационального $alpha$ . Как такое может быть, там же дискриминант и всё такое? Ладно, попробуем:

$D=b^2 - 4 a c=1 ^ 2 + 4 alpha (1 + alpha)=1 + 4 alpha + 4 alpha ^ 2=(1+2 alpha)^2$

О-о-о, хорошо-то как, полный квадрат вышел. Эндорфин в мозг ^[1] пошёл. Он, наркоман эдакий, похоже этого и добивался. Вот она магия математики: должно было выйти рациональное число и вышло. Вспоминаем формулы для корней:

$p_{1,2}=frac {-b pm sqrt D} {2 a}$

Или в наших обозначениях:

$p_1=frac{1 - (1+2 alpha)} {2 alpha}=-1$

$p_2=frac{1 + (1+2 alpha)} {2 alpha}=frac{1 + alpha} alpha$

$p_1$ — это наша опорная точка, $-1$ , это нам неинтересно. Наше решение — это $p_2$ . Подставив его в $q=alpha(p+1)$ получаем ответ:

$p=frac{1 + alpha} alpha; q=1 + 2 alpha$

То есть надо просто перебрать все рациональные дроби в качестве $alpha$ , и для них мы получим все рациональные решения уравнения $1 + p + q - pq=0$ (ну кроме некоторых, которые нам не очень интересны).

Разумеется, перебирать проще целые числа, а не рациональные. Спаивая младенцу препарат симетикона, я подставляю $alpha=m/n$ и получаю:

$p=frac{1 + frac m n} {frac m n}=frac {n + m} m$

$q=2 + frac m n=frac {n + 2m} n$

(Боже, мозг ^[1], зачем ты выбрал именно $m$ и $n$ ? Они так легко путаются в голове! Букв мало что ли?) В нашем юнит-тесте, если $alpha=1$ , то подойдут $m=n=1$ и легко убедиться, что тест проходит.

Как нам вернуться к целым числам? Вспоминаем, что мы заменили $p=a / x; q=b / x$ . Значит, надо принять за $x$ любое число, кратное общему знаменателю из формул выше. В частности, подходит просто $mn$ . В итоге имеем:

$x=mn; a=mn + n^2; b=mn + 2m^2$

Видно, что если $m$ и $n$ не взаимно простые, то и решение будет кратно их общему делителю, поэтому нам интересны только взаимно простые $m$ и $n$ . Кратное решение также получится, если $n$ окажется чётным. В самом деле пусть $n=2n'$ . Тогда

$x=2mn'; a=2mn' + 4n'^2; b=2mn' + 2m^2$

Если поделить всё на два, то получим

$x=mn'; a=mn' + 2n'^2; b=mn' + m^2$

Это решение симметрично первому, что вполне логично: ведь задача симметрична относительно $a$ и $b$ . Таким образом, нам интересны взаимно простые $m$ и $n$ , причём $n$ нечётно.

Удобно, что выражение для $x$ получилось таким простым. Значит, у нас есть простой способ найти все некратные решения для заданной наперёд ширины окантовки $x$ : это такие прямоугольники $a=x + n^2; b=x + 2(x/n)^2$ , где $n$ любой нечётный делитель $x$ , взаимно простой с $x/n$ . Следующий прямоугольник будет для $x=2; n=1; m=2; a=3; b=10$ :

Мозаика в ванной и диофантовы уравнения - 87

И голубая, и жёлтая часть содержат ровно по 30 клеточек!

Давайте посмотрим, какие ещё есть решения для маленьких $x$ ( $a$ и $b$ я кое-где переставил, чтобы шли по возрастанию):

x	n	m	площадь без окантовки	площадь с окантовкой
1	1	1	2 × 3 = 6	3 × 4 = 12
2	1	2	3 × 10 = 30	5 × 12 = 60
3	1	3	4 × 21 = 84	7 × 24 = 168
3	3	1	5 × 12 = 60	8 × 15 = 120
4	1	4	5 × 36 = 180	9 × 40 = 360
5	1	5	6 × 55 = 330	11 × 60 = 660
5	5	1	7 × 30 = 210	12 × 35 = 420
6	1	6	7 × 78 = 546	13 × 84 = 1092
6	3	2	14 × 15 = 210	20 × 21 = 420

Насчитывая в голове эти произведения, мозг ^[1] снова добился дозы эндорфина. Как красиво и чудесно делители перетекают из одного числа в другое! Взять, например, $6 times 55$ : первое делится на 6, а второе на 11. Добавляем к обоим числам пятёрку, и чудо — теперь первое делится на 11, а второе — на 6. И такие фокусы в каждой строчке! А тут и сын вроде успокоился. Одиннадцать вечера, можно и спать ложиться.

Возможно, это всё можно посчитать проще. Возможно, мои рассуждения были где-то неточными. Возможно, у этих чисел и произведений есть какое-то специальное название. Я не знаю — не искал. Мне больше вот что интересно: я один такой чушью занимаю своё сознание, или вы тоже этим ~~страдаете~~ наслаждаетесь? Нас вылечат?

Автор: Тагир Валеев

Источник ^[4]

Сайт-источник PVSM.RU: https://www.pvsm.ru

Путь до страницы источника: https://www.pvsm.ru/matematika/274683

Ссылки в тексте:

[1] мозг: http://www.braintools.ru

[2] диофантово уравнение: https://ru.wikipedia.org/wiki/%D0%94%D0%B8%D0%BE%D1%84%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D0%BE_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5

[3] пифагоровых троек: https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D1%84%D0%B0%D0%B3%D0%BE%D1%80%D0%BE%D0%B2%D0%B0_%D1%82%D1%80%D0%BE%D0%B9%D0%BA%D0%B0

[4] Источник: https://habrahabr.ru/post/350640/?utm_source=habrahabr&utm_medium=rss&utm_campaign=350640

Нажмите здесь для печати.