Предыстория
В 3D имеется объемная фигура с триангулированной поверхностью и требуется выяснить: находится ли некоторая данная точка внутри объема или снаружи… Вот если бы речь шла об аналитически заданной поверхности или об объединении и пересечении таких поверхностей, то всё просто — втыкаем нашу точку в аналитическую функцию поверхности f (x,y,z) = 0 и смотрим: ноль или не ноль? Если больше нуля, то точка снаружи (куда градиент показывает), а если меньше нуля, то внутри. Да и с триангулированной поверхностью тоже особой возни нет, просто чуть дольше:
— выбираем тестовую точку, которая заведомо лежит например снаружи,
— соединяем ее отрезком с некоторой данной точкой (про которую мы хотим узнать, внутри она или снаружи)
— и перебираем все треугольники, считаем пересечения: пересечений четное число — значит точка снаружи (как и тестовая, выбранная нами), нечетное — внутри.
Осталось только сообразить, как пересечения c треугольниками фиксировать. И давайте немного договоримся с терминологией: пересечением будем называть наше рабоче-крестьянское пересечение, когда отрезок уверенно пронзает треугольник, а не трусливо по-интеллигентски его всего лишь касается).
История
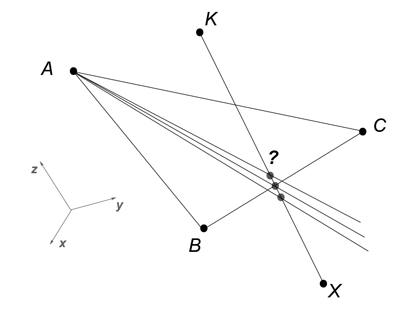
Даны: треугольник ABC и отрезок KX. Принцип у нас будет простой. Через точки A, B, C, K проведем 4 плоскости нормалями наружу и спросим у каждой, лежит ли точка X под ней или над ней. Если X лежит под всеми плоскостями, значит пересекаются наш отрезок KX и наш треугольник ABC. Ну а если нет, то извиняйте.
Алгоритм
1. Вычисляем векторы (разность векторов):
KA= A-K
KB= B-K
KC= C-K
AB= B-A
AC= C-A
2. Вычисляем смешанное произведение alpha (скалярное и векторное произведения векторов):
alpha= (KA,[ KB,KC ])
3. Вычисляем нормали плоскостей n0, n1, n2, n3 (векторное произведение векторов):
n0= [AB, AC]
n1= [KA, KB]
n2= [KB, KC]
n3= [KC, KA]
4. Ориентируем нормали наружу (умножение скаляра на вектор):
n0= -alpha*n0
n1= -alpha*n1
n2= -alpha*n2
n3= -alpha*n3
5. Вычисляем свободное слагаемое в уравнениях плоскостей (скалярное умножение векторов):
d0= -(n0, A)
d1= -(n1, K)
d2= -(n2, K)
d3= -(n3, K)
6. Вычисляем значение функции плоскостей в искомой точке X (скалярное произведение векторов плюс скаляр):
F0= (n0, X) + d0
F1= (n1, X) + d1
F2= (n2, X) + d2
F3= (n3, X) + d3
7. Анализируем (alpha, F0, F1, F2, F3):
7.0 Если alpha = 0, то точка K лежит в плоскости треугольника (внутри или снаружи треугольника -неизвестно, можно повторить алгоритм инвертировав отрезок), в любом случае отрезок не пересекается с треугольником, возможно лишь, что его концы принадлежат треугольнику. Далее рассматриваем случаи, если alpha НЕ равна нулю
7.1 Если максимум (F0, F1, F2, F3) < 0, то отрезок KX пересекается с треугольником ABC
7.2 Если максимум (F0, F1, F2, F3) > 0, то отрезок KX НЕ пересекается с треугольником ABC
7.3 Если максимум (F0, F1, F2, F3)=0, то (вот он! гадкий интеллигентский случай полукасаний и недопроникновений):
7.3.1 Если F0 =0, то X принадлежит треугольнику (лежит внутри или на ребре треугольника)
7.3.2 Если F1 или F2 или F3 = 0 то отрезок касается границы треугольника, а именно:
7.3.2.1 одна из F равна нулю, остальные — меньше нуля: отрезок пересекается с ребром
7.3.2.2 две из F равны нулю, одна — меньше нуля: отрезок содержит вершину треугольника
Послесловие
1. По поводу первоначальной задачи про 3D-поверхность. Точку K мы заведомо возьмем за пределами триангулированной поверхности, она никакому треугольнику принадлежать не будет. Далее в алгоритме введем переменную flag и будем ей присваивать значения в соответствии со случаями:
7.0 flag = 0
7.1 flag = -alpha / |alpha| (эту конструкцию назовем: «минус знак альфы», равняется она "-1" или "+1", если сама альфа не равна нулю конечно, но этот противный случай мы рассмотрели в 7.0)
7.2 flag = 0
7.3.1 flag = 0
7.3.2.1 flag = -0,5*alpha / |alpha|
7.3.2.2 flag = -0,001*alpha / |alpha|
Потом просуммируем флаги от всех треугольников и… предлагаю подумать.
2. Вместо треугольника можно взять кусочек не плоской аналитической поверхности. Тоже получается. Только у кривых аналитических поверхностей обычно бывает «задняя» сторона, это надо учесть.
Автор: FransuaMaryDelone