Первая часть
Первая часть второй части
Майские праздники продолжаются, количество употреблений слова «часть» на строку текста зашкаливает, а мы с вами, дорогие читатели, наконец прикончим случай поворота с центром внутри фигуры.
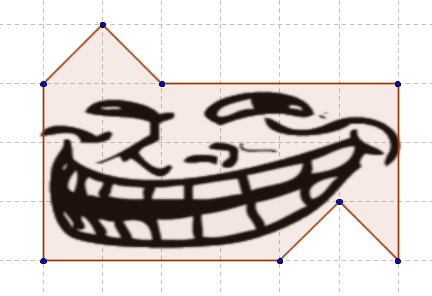
Случай 2.2: центр поворота внутри фигуры
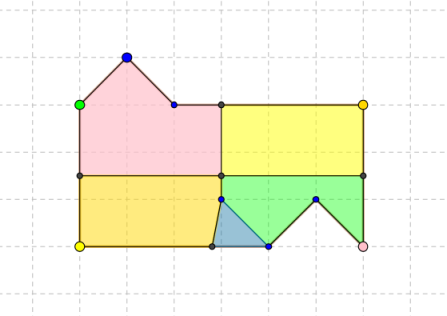
Для начала используем свойство дальнего граничного сечения. Если это предложение для вас бессмысленный набор букв, вам следует ознакомиться с предыдущими двумя частями. Если нет — то вот красивая цветная картинка, являющаяся, по сути, продолжением аналогичной картинки из предыдущей части. Напомню: каждая из цветных областей — геометрическое место точек, для которых, будь они центром поворота, граничное сечение состояло бы из одной-единственной вершины, покрашенной соответствующим цветом. Поскольку сечение не может состоять из единственной точки (см. лемму 1), центр поворота может располагаться лишь на границе между областями. Таким образом, множество возможных положений центра поворота сужается до набора отрезков. Далее мы постараемся сузить его до пустого множества.
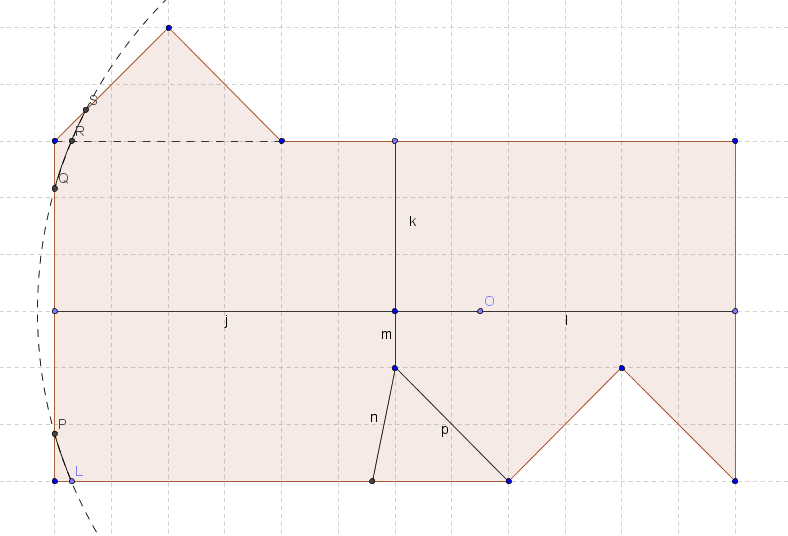
Из-за отсутствия внутренней границы (и связанного с ней критерия) мы не можем расправиться с этим случаем так лихо, как со случаем центра вне фигуры. Однако кое-что мы всё-таки можем. Начнём со следующего рассуждения: возьмём секущую чуть-чуть меньшего радиуса, чем внешняя граница. Тогда сечение (по крайней мере, в случае данной конкретной фигуры) будет состоять из двух или более маленьких-маленьких дуг. Поскольку их угловая мера будет меньше, чем угол поворота, при отображении из B в C им ничего не остаётся, кроме как переходить друг в друга. Соответственно, если у нас есть ровно две маленькие дуги — значит, эти дуги должны иметь равную угловую меру. Покажем, что в случае нашей фигуры этот критерий систематически нарушается.
Возьмём произвольную точку О на отрезке i и назначим её центром. Проведём секущую слегка меньшего радиуса, чем внешняя граница. Тогда сечение будет состоять из двух достаточно маленьких дуг: LP и QS. При этом QS = QR + RS. Однако LP = QR в силу симметрии. Следовательно, LP ≠ QS, а значит, точка О никак не может быть центром поворота.
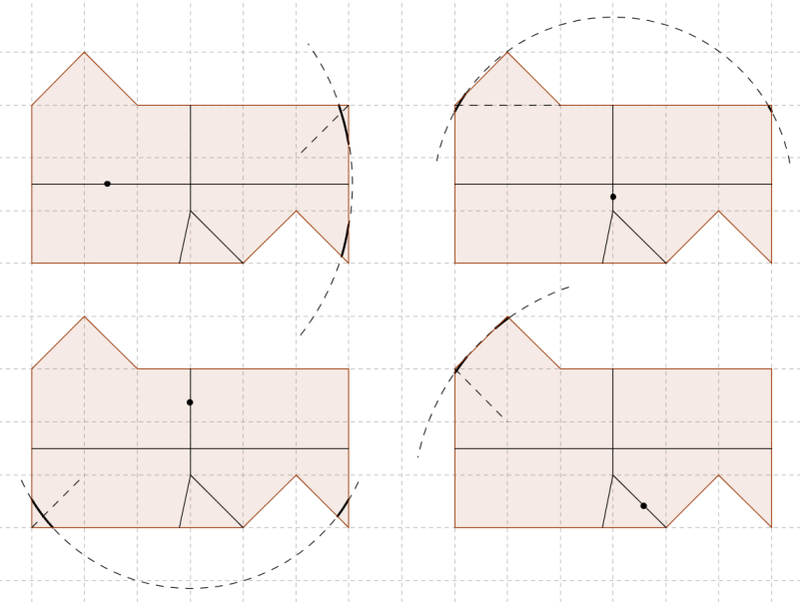
Аналогичный фокус мы можем провернуть с отрезками j, k, m, p. В целях хоть какой-то разборчивости я убрал с чертежа всё лишнее, но всё равно ни хрена не понятно, поскольку, как уже говорилось выше, дуги очень-очень маленькие. Пунктирные дуги, очевидно, части секущих; жирным выделены, собственно, сечения. Пунктирные отрезочки — это те самые хитрые отрезочки, которые, аналогично случаю отрезка i, отделяют от одной из дуг сечения кусок, равный другой дуге, показывая тем самым, что целиком первая дуга будет больше второй.
Остаётся отрезок n, для которого не удаётся так удобно показать неравенство маленьких дуг. Ввиду этого нам потребуется слегка расширить имеющийся математический аппарат, добавив в него следующую лемму:
Лемма 3. Для каждой точки фигуры A её образ или прообраз также принадлежит фигуре A.
Доказательство: очевидно. Пусть точка принадлежит фигуре В, тогда её образ принадлежит фигуре С и, следовательно, фигуре А. Аналогично, если точка принадлежит фигуре С.
Что нам даёт эта лемма? А то, что нам достаточно найти точку, которая принадлежит нашей фигуре, но при повороте на соответствующий угол по и против часовой стрелки перестаёт ей принадлежать. Такая находка будет означать, что данный поворот не годится.
Для этих грязных целей мы возьмём точку K. Если двигать центр поворота O по отрезку n, то образы точки K при повороте на плюс-минус угол POQ будут двигаться по соответствующим жирным дугам соответствующих пунктирных окружностей (здесь нелишне будет уточнить, что точки P и Q суть граничное сечение для центра, лежащего на отрезке n, и, соответственно, угол POQ — это как раз угол поворота). Нетрудно заметить, что эти дуги ни разу не пересекаются с фигурой A0. Следовательно, центр поворота не может располагаться на отрезке n.
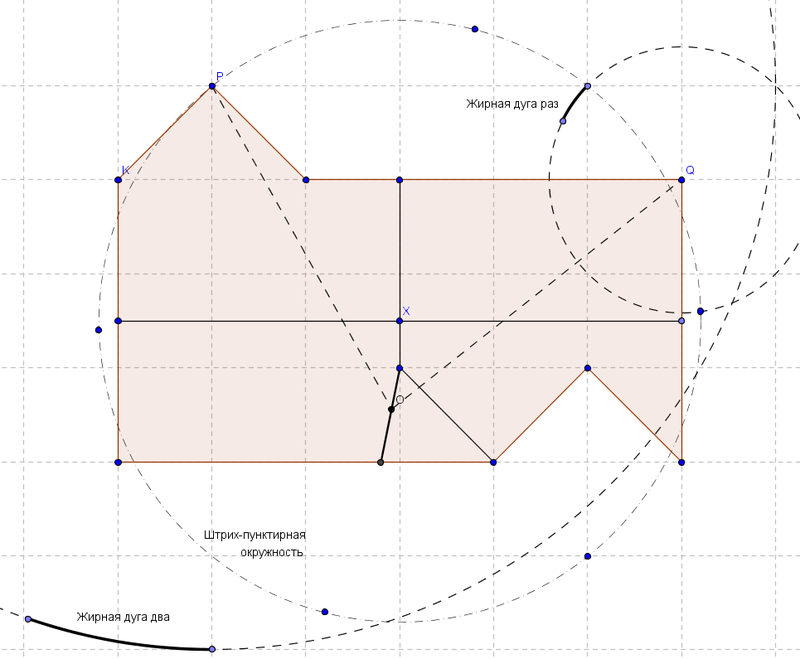
Обратите также внимание на штрих-пунктирную окружность, на которой располагается точка P и отмечено ещё пять безымянных точек (конец «жирной дуги раз» не считается, он туда попал случайно). Дело в том, что точка X, которая находится в центре фигуры — особенная. Для неё граничное сечение будет состоять не из двух, а аж из четырёх точек — соответственно, доказательство на основе «маленьких дуг» для неё не работает. Однако доказательство на основе леммы 3 работает замечательно. Пять безымянных точек на штрих-пунктирной окружности — это образы точки Р при всех возможных поворотах, соответствующих граничному сечению, соответствующему точке Х (я извиняюсь за злоупотребление словом «соответствующий»). Ни один из этих образов не попадает в фигуру А0 — следовательно, точка Х также исключается.
Есть ещё одна особая точка с особым граничным сечением. Предоставляю внимательным читателям право найти её и доказать, что она также не может быть центром поворота. Это несложно.
Вывод
Если фигуру A0 и можно разрезать на две равные фигуры В и С, то В не переводится в С ни параллельным переносом, ни поворотом. Остаётся лишь скользящая симметрия. Последняя статья цикла, в которой я разберу и этот случай, будет опубликована 9 мая, что как бы символизирует окончательную победу над задачей, наделавшей в своё время столько шороха.
Автор: Sirion








