Пусть p — нечётное простое число. Довольно широко известно, что p представимо в виде суммы двух квадратов целых чисел p=a2+b2 тогда и только тогда, когда p при делении на 4 даёт остаток 1: 5=12+22, 13=32+22, 17=12+42, ...; 3, 7, 11,… непредставимы. Куда менее известно, что a и b можно записать красивой формулой, имеющей непосредственное отношение к одной эллиптической кривой. Об этом результате 1907 года за авторством немца по фамилии Jacobsthal и о связанных вещах мы сегодня и поговорим.
Совсем легко понять, почему 3, 7, 11 и прочие числа, дающие при делении на 4 остаток 3, непредставимы в виде a2+b2: квадрат чётного числа всегда делится на 4, квадрат нечётного числа всегда даёт остаток 1 при делении на 4, сумма двух квадратов при делении на 4 может давать остатки 0, 1 или 2, но никак не 3. Представимость простых чисел вида 4k+1 неочевидна (особенно если заметить, что простота существенна: число 21 хотя и имеет нужный остаток, но суммой двух квадратов не представляется).
Вычеты
Натуральных чисел бесконечно много. Бывает полезно объединять их в классы по каким-нибудь признакам. В частности, объединение по остатку от деления на какое-нибудь число n приводит к вычетам по модулю n: вычет x̅ — это класс всех чисел, которые при делении на n дают тот же остаток, что и x. Что эквивалентно, вычет x̅ состоит из всех чисел вида x+n∙k, где k целое. В рамках данного поста все вычеты будут по модулю p (того самого нечётного простого числа из введения). Естественно, различных вычетов столько же, сколько может быть остатков от деления на p, то есть ровно p. По сравнению с бесконечностью натуральных чисел переход к вычетам сильно сокращает число вариантов.
Операции над классами далеко не всегда имеют смысл. Например, попытка сложить класс простых чисел с классом составных чисел не очень осмысленна: мы умеем складывать только числа, а у суммы простого числа и составного числа не видно свойств, общих для класса. Хотя члены клуба тавтологии и могут сказать, что сложение класса простых чисел и класса составных чисел даёт класс чисел, раскладывающихся в сумму простого числа и составного числа.
Для вычетов, тем не менее, сложение, вычитание и умножение, «унаследованные» от натуральных чисел, дают другие вычеты. Например, 2̅+3̅=5̅: возьмём любое число с остатком 2, любое число с остатком 3, и их сумма обязательно даст остаток 5. Вообще говоря, произведение двух ненулевых вычетов по произвольному модулю может внезапно оказаться нулём, 2̅∙3̅=0̅ по модулю 6, что неприятно. Но в случае простого модуля, очевидно, такого не бывает, как говорят, нет делителей нуля. Кроме того, можно решить уравнение a̅∙x̅=b̅ (операция деления) для любых двух вычетов, кроме случая a̅=0̅, и результат будет однозначно определён. Однозначность следует из того, что произведение ненулевых вычетов ненулевое. Поскольку a̅≠0̅, то наибольший общий делитель a и p равен 1 (здесь тоже нужна простота p), расширенный алгоритм Евклида найдёт x и y такие, что a∙x+p∙y=1, откуда следует a̅∙x̅=1̅, а значит, a̅∙(b̅∙x̅)=b̅.
Важное следствие из отсутствия делителей нуля: ненулевой многочлен от одной переменной степени n не может иметь более n корней. (Это хорошо известно для обычных целых чисел, но при использовании операций над вычетами требует дополнительного обоснования: уравнение 3̅∙x̅=0̅ по модулю 6 имеет три решения 0̅, 2̅, 4̅.) Действительно, обычное деление «в столбик» показывает, что любой многочлен f(x) можно представить в виде f(x)=(x-с)g(x)+(некоторая константа), где многочлен g(x) имеет степень на единицу меньше; если c — это корень f(x), то константа равна нулю (подставим x=c); если c' — другой корень f(x), то он будет корнем g(x) (здесь важно отсутствие делителей нуля), так что процесс можно продолжить. Если уже набралось n корней, то оставшийся g(x) будет константой, причём ненулевой (иначе f(x)=0) и больше корней не имеет.
Вычеты по простому модулю можно складывать, вычитать, умножать. На ненулевые вычеты можно делить. Все эти операции обладают обычными свойствами типа a̅∙b̅=b̅∙a̅. В умных книгах говорят, что вычеты по простому модулю образуют поле (а вычеты по составному модулю, где делить нельзя, а всё остальное такое же, — коммутативное кольцо). И не надо быть умной книгой, чтобы назвать это поле конечным. Поле вычетов — не единственное конечное поле, но другие конечные поля нам не понадобятся.
Чуть-чуть про эллиптические кривые
Эллиптическую кривую по модулю p (тому самому нечётному простому числу) можно рассматривать как набор решений уравнения y2=x3+a2x2+a4x+a6, где x, y и все a — вычеты (каждое решение называется одной точкой), плюс одна специальная точка O, не имеющая пары x, y. Правая часть уравнения не должна делиться на квадрат, иначе это будет не эллиптическая кривая: в уравнении типа y2=(x-1̅)2(x+2̅) можно переменную y заменить на z=y/(x-1̅) и получить зависимость второй степени, а не третьей.
Если p≠3, то вместо переменной x можно взять x+a2/3̅, избавившись от члена с x2.
Ясно, что раз x, y принадлежат конечному множеству, то число точек на эллиптической кривой тоже конечно. Сколько их? Это сложный в общем случае вопрос. Мы ограничимся кривыми вида y2=x3-k∙x. Для таких кривых полное доказательство можно уложить в один пост Хабра (хотя и довольно длинный).
Квадратичные вычеты и невычеты
Зададимся сначала более простым вопросом. Сколько решений есть у уравнения y2=c, где y, c — вычеты? Пример для p=7:
| y | 0̅ | 1̅ | 2̅ | 3̅ | 4̅ | 5̅ | 6̅ |
| y2 | 0̅ | 1̅ | 4̅ | 2̅ | 2̅ | 4̅ | 1̅ |
Если c=0̅, то решение одно, y=0̅. Остальные значения y разбиваются на две половины, от 1̅ до вычета, соответствующего (p-1)/2, и от вычета, соответствующего (p+1)/2, до -1̅. Раз y2=(-y)2, вторая половина строки значений y2 зеркально-симметрична первой половине. С другой стороны, в каждой половине повторений нет, поскольку иначе у уравнения было бы как минимум 4 решения, что невозможно для многочлена степени 2. Значит, есть (p-1)/2 вычетов c, для которых решений ровно 2, и столько же вычетов c, для которых решений нет совсем.
Ненулевые вычеты c, для которых есть решение, называются квадратичными вычетами. Вычеты c, для которых решения нет, называются квадратичными невычетами. Стоит отметить, что квадратичный невычет — это таки вычет, просто ему не повезло быть квадратичным. Символ Лежандра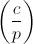 
показывает отношение c к квадратам: 1, если относится (то есть c — квадратичный вычет), -1, если не относится (то есть c — квадратичный невычет), 0, если c=0̅. Число решений уравнения y2=c равно 
.
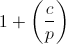Вернёмся к эллиптическим кривым. Число вариантов y для фиксированного x мы знаем, общее число точек на кривой y2=x3-k∙x можно записать, просуммировав по всем x и не забыв про специальную точку: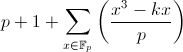 
. Символом Fp, который раньше не появлялся, принято обозначать поле (field) вычетов по модулю p.
Теперь мы готовы предъявить обещанные формулы для компонентов разложения p в сумму двух квадратов. Теорема. Пусть g — любой квадратичный невычет. Если p при делении на 4 даёт остаток 1, то
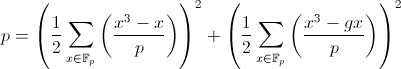
причём число в первой скобке целое нечётное, число во второй скобке целое чётное. Если же p при делении на 4 даёт остаток 3, то обе суммы в скобках нулевые (а значит, число точек на эллиптических кривых равно p+1).
Доказательство
Поскольку пост и без того длинный, доказательство убрано под спойлер. Его можно спокойно пропустить без ущерба для восприятия.
Значит, многочлен xp-1-1=(x(p-1)/2-1)(x(p-1)/2+1) имеет p-1 корней. Значит, каждая скобка имеет (p-1)/2 корней (максимально возможное количество для степени скобок). Каждый квадратичный вычет — корень первой скобки (если x=c2, то x(p-1)/2=cp-1=1̅), их (p-1)/2, значит, всем квадратичным невычетам остаётся вторая скобка. Итак, символ Лежандра от c принадлежит тому же вычету, что и c(p-1)/2. (Это было доказательство критерия Эйлера).
Как следствие, получаем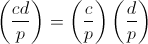 
.
Является ли -1̅ квадратичным вычетом? Зависит от знака (-1)(p-1)/2. Если p при делении на 4 даёт остаток 1, то (p-1)/2 чётно, (-1)(p-1)/2=1, -1̅ — квадратичный вычет. Если p при делении на 4 даёт остаток 3, то всё наоборот и -1̅ — квадратичный невычет.
Простая часть теоремы: p даёт остаток 3 при делении на 4. Тогда в каждой скобке слагаемые с x и -x отличаются друг от друга умножением на символ Лежандра от -1̅, то есть противоположны по знаку и в сумме дают 0. Поскольку все слагаемые, кроме x=0̅, разбиваются на пары с нулевой суммой, а слагаемое с x=0̅, нулевое, вся сумма равна 0.
Если p даёт остаток 1 при делении на 4, то слагаемые с x и -x равны и их сумма четна. Значит, вся сумма также четна и числа в скобках действительно целые. Чётность/нечётность после деления пополам ненамного сложнее: в первой скобке теоремы есть три нулевых слагаемых, остальные слагаемые разбиваются на (p-3)/2 пар с суммой ±2 в каждой паре; при любом знаке при делении на 4 получается остаток 2, вся сумма при делении на 4 даёт остаток такой же, как p-3, то есть 2. После деления пополам получим нечётное число. Во второй скобке теоремы всего одно нулевое слагаемое и (p-1)/2 пар с ±2, итоговый остаток от деления на 4 получается 0, после деления пополам остаётся чётное число.
Для доказательства посчитаем двумя способами следующую странную величину N: число пятёрок вычетов (x1, y1, x2, y2, t) таких, что выполнены сразу два уравнения: y12=x13-t∙x1 и y22=x23-t∙x2.
В первом способе сначала зафиксируем t и посчитаем число четвёрок из x, y, после чего сложим результаты для всех t. Ясно, что при фиксированном t пара (x1, y1) может быть любой неспециальной точкой кривой y2=x3-t∙x, вторая пара (x1, y1) — столь же любой неспециальной точкой той же кривой, а общее число таких пар равно квадрату числа неспециальных точек. (Собственно, поэтому мы и рассматриваем странную величину, она позволяет подобраться к a2 и b2.) Если t=0, то уравнение y2=x3, как уже говорилось, не задаёт эллиптическую кривую и имеет столько же решений, сколько уравнение z2=x (где y=z∙x), то есть ровно p. При t=1 получается p+2a решений, при t=g — p+2b решений. Что насчёт остальных значений t?
Если y2=x3-t∙x и c — какой-то ненулевой вычет, то c6y2=c6x3-c6t∙x, что эквивалентно (c3y)2=(c2x)3-c4t∙(c2x). Иными словами, если (x,y) — решение уравнения с t, то (c2x,c3y) — решение уравнения с c4t, так что число решений с t и с c4t совпадает. Сколько есть разных ненулевых вычетов вида c4? С одной стороны, не менее (p-1)/4: (p-1) значений c могут «склеиваться» в группы размером не более 4. С другой стороны, если (p-1)/4 — целое число, то все такие вычеты — корни многочлена x(p-1)/4-1, так что их не может быть больше (p-1)/4. Значит, их ровно (p-1)/4.
Итак, (p-1)/4 кривых имеют p+2a неспециальных точек, ещё (p-1)/4 кривых имеют p+2b неспециальных точек. Это уже половина всего, что надо.
Если y2=x3-t∙x, то g3y2=(g∙x)3-(g2t)(g∙x). При фиксированном x число решений уравнения g3y2=... равно 2 — число решений уравнения y2=.... Значит, число неспециальных точек на кривой с t=g2 (а следовательно, на (p-1)/4 подобных кривых) равно 2p-(p+2a)=p-2a. Аналогично число неспециальных точек на кривой с t=g3 равно 2p-(p+2b)=p-2b.
Итак, первый способ вычисления даёт
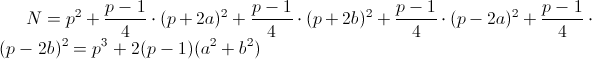
Во втором способе вычисления N сначала зафиксируем x1 и x2 и посчитаем число троек t и y, после чего сложим результаты для всех пар x. При x1=x2=0̅ есть ровно p вариантов: оба y должны быть нулями, t может быть любым. При x1=0̅ и ненулевом x2 должно быть y1=0, y2 может быть любым, t вычисляется однозначно, получается снова p вариантов. Ситуация с нулевым x2 и ненулевым x1 симметрична. Наконец, пусть оба x ненулевые. Тогда t=x12-(y12/x1) и нужно посчитать число пар y с условием (x2/x1)y12=y22+x2(x12-x22).
Если x1=x2, то уравнение превращается в условие совпадения квадратов y, и различных пар y получается 1+2(p-1): нулевая и по два варианта y2 для каждого ненулевого y1. Если x1=-x2, ситуация аналогичная, поскольку p даёт остаток 1 при делении на 4 и -1̅ — квадратичный вычет.
Если x2/x1 — квадратичный вычет, не равный ±1̅, то существует какое-то ненулевое c такое, что c2=x2/x1. Тогда (c2y12-y22)=(c∙y1-y2)(c∙y1+y2)=x2(x12-x22), выражение c∙y1-y2 может быть любым ненулевым вычетом, по нему однозначно определяется c∙y1+y2 и, следовательно, y1 и y2. Итого p-1 вариантов.
Если x2/x1 — квадратичный невычет, то аналогично эллиптическим кривым число решений равно 2p минус число решений в случае квадратичного вычета, то есть 2p-(p-1)=p+1.
Суммируем. Есть один вариант с x1=x2=0, дающий p решений. Есть 2(p-1) вариантов, где один из x нулевой, а другой ненулевой, каждый из вариантов даёт p решений. Есть 2(p-1) вариантов с x2=±x1, каждый из которых даёт 2p-1 решений. Есть (p-1)((p-1)/2-2) вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный вычет, отличный от ±1̅, каждый из этих вариантов даёт p-1 решений. Наконец, остаётся (p-1)2/2 вариантов, где x1 — произвольный ненулевой вычет, а x2/x1 — квадратичный невычет, в каждом из этих вариантов p+1 решений. Итого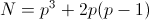 
.
Сравнение двух выражений для N завершает доказательство.
Причём здесь криптография?
Вычислять a и b, подсчитывая p раз символы Лежандра, непрактично. Куда быстрее с этим справится алгоритм Cornacchia. Практическая польза — использовать формулу для a, b в обратную сторону: можно доказать, что разложение p=a2+b2 единственно с точностью до перестановки a и b и смены знаков, так что нахождение a и b влечёт знание числа точек на кривых y2=x3-t∙x для любого ненулевого t, это будет p+1±2a и p+1±2b.
Знание числа точек на кривой важно для криптографии на этой кривой. На эллиптической кривой можно ввести операцию сложения точек (о чём слышали, наверное, все, кто хоть что-то знает о криптографии) со специальной точкой O в роли нуля. На основе операции сложения можно определить умножение на натуральное число: 2P=P+P, 3P=P+P+P и так далее. Так вот, можно доказать, что если n — порядок кривой, то nP=O для любой точки P. Зная n, c, d, можно решать уравнения вида x∙(cP)=dP полностью аналогично делению вычетов: расширенный алгоритм Евклида найдёт x, y такие, что c∙x+n∙y=1, откуда x∙(cP)+y∙(nP)=P, то есть x∙(cP)=P. При этом, если c, d неизвестны, а cP и dP заданы координатами, то эффективных методов деления в общем случае неизвестно.
Вычислить число точек на заданной кривой довольно сложно (полиномиальный алгоритм существует, но на практике довольно медленный). Чтобы построить кривую с какими-нибудь свойствами на число точек, можно пытаться взять случайные коэффициенты и вычислять число точек в цикле, пока не получится то, что надо, но придётся подождать. К счастью, есть другой способ.
Если нас устраивает простое число вида 4k+1 и кривая специального вида y2=x3-t∙x (в некотором смысле это одна и та же кривая при любом ненулевом t) с числом точек p+1±2a или p+1±2b, можно её и взять. Что насчёт других кривых?
Немного позднее, в 1911 году, уже другой автор von Schrutka получил аналогичный результат для кривых вида y2=x3-t, простых вида 6k+1, представления p=a2+3b2. Значит, найти число точек на кривой y2=x3-t опять же позволяет алгоритм Cornacchia.
Позднее, по мере развития теории эллиптических кривых, выяснилось, что если есть какое-то представление 4p=a'2+d∙b'2, где d натуральное, при делении на 4 даёт остаток 0 или 3, взаимно простое с p и не слишком большое, то можно эффективно (даже если p очень большое) построить кривую, которая будет иметь ровно p+1±a' точек. Два наименьших значения d=3 и d=4 соответствуют кривым y2=x3-t и y2=x3-t∙x. Пример для d=163:
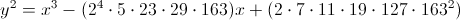
При нечётном p≠163 это уравнение задаёт эллиптическую кривую. Если 4p представимо в виде a'2+163b'2 с целыми a', b', то число точек на эллиптической кривой равно p+1±a'. Если нет, то p+1. К сожалению, доказательство использует «тяжёлую» теорию, поэтому здесь не будет даже намёков.
Обычно, впрочем, будут получаться радикалы. Например, для d=15: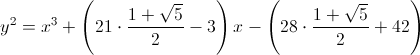 
. Если 4p раскладывается в сумму a'2+d∙b'2 и p взаимно просто с d, то все радикалы обязательно извлекутся (например, для d=15 обязательно найдётся вычет c, для которого c2=5̅ ) и получится эллиптическая кривая с нужным числом точек.
Автор: grechnik
