Сумма всех натуральных чисел: 1 + 2 + 3 + 4 +…

Сумма всех натуральных чисел может быть записана с использованием следующего числового ряда

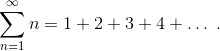
Чему равна сумма этого бесконечного ряда? Перед тем, как читать дальше, дайте себе минуту на размышления. Если вы до этого не встречались с подобным рядом, а тема численных рядов в целом не слишком вам близка, то ответ на этот вопрос будет для вас большим сюрпризом.

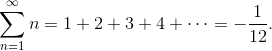
Этот, на первый взгляд, совершенно противоречащий интуиции результат, тем не менее может быть строго доказан. Но прежде, чем говорить о доказательстве, нужно сделать отступление и вспомнить основные понятия.

Начнём с того, что «классической» суммой ряда ^[1] называется предел частичных сумм ряда, если он существует и конечен. Подробности можно найти в википедии и соответствующей литературе. Если конечный предел не существует, то ряд называется расходящимся.

Например, частичная сумма первых k членов числового ряда 1 + 2 + 3 +4 +… записывается следующим образом

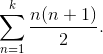
Нетрудно понять, что эта сумма неограниченно растёт при стремлении k к бесконечности. Следовательно, исходный ряд является расходящимся и, строго говоря, не имеет суммы. Существует, однако, множество способов присвоить конечное значение расходящимся рядам.

Ряд 1+2+3+4+… далеко не единственный из расходящихся рядов. Возьмём, например, ряд Гранди ^[2]

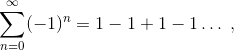
который тоже расходится, но известно, что метод суммирования Чезаро ^[3] позволяет присвоить этому ряду конечное значение 1/2. Суммирование по Чезаро заключается в оперировании не частичными суммами ряда, а их арифметическими средними. Позволив себе порассуждать в вольном стиле, можно сказать, что то частичные суммы ряда Гранди осцилируют между 0 и 1, в зависимости от того какой член ряда является последним в сумме (+1 или -1), отсюда и значение 1/2, как арифметическое среднее двух возможных значений частичных сумм.

Другим интересным примером расходящегося ряда является знакопеременный ряд 1 — 2 + 3 — 4 +... ^[4], частичные суммы которого также осцилируют. Суммирование методом Абеля позволяет присвоить данному ряду конечное значение 1/4. Отметим, что метод Абеля является, своего рода, развитием метода суммирования по Чезаро, поэтому результат 1/4 несложно осмыслить с точки зрения интуиции.

Здесь важно отметить, что методы суммирования не являются трюками, которые придумали математики, чтобы как-то совладать с расходящимися рядами. Если вы примените суммирование по Чезаро или метод Абеля к сходящемуся ряду, то ответ, который дают эти методы, равен классической сумме сходящегося ряда.

Ни суммирование по Чезаро, ни метод Абеля, однако, не позволяют работать с рядом 1 + 2 + 3 + 4 +..., т. к. средние арифметические частичных сумм, равно как и средние арифметические средних арифметических, расходятся. Кроме того, если значения 1/2 или 1/4 ещё как-то можно принять и соотнести с соответствующими рядами, то -1/12 сложно связать с рядом 1 + 2 + 3 + 4 +..., представляющим собой бесконечную последовательность положительных целых чисел.

Существует несколько способов прийти к результату -1/12. В этой заметке я лишь кратко остановлюсь на одном из них, а именно регуляризации дзета-функцией ^[5]. Введём дзета-функцию

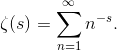
Подставляя s = -1, получим исходный числовой ряд 1+2+3+4+…. Проделаем над этой функцией ряд несложных математических действий

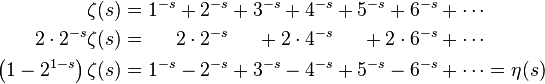
Где 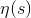является эта-функцией Дирихле ^[6]

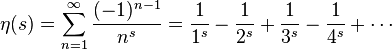
При значении s = -1 эта-функция становится уже знакомым нам рядом 1 — 2 + 3 — 4 + 5 -… сумма которого равна 1/4. Теперь мы можем легко решить уравнение

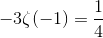
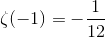
Интересно, что этот результат находит своё применение в физике. Например, в теории струн. Обратимся к стр. 22 книги Joseph Polchinski «String Theory»:

Если для кого-то теория струн не является убедительным примером в силу отсутствия доказательств множества следствий этой теории, то можно также упомянуть, что похожие методы фигурируют в квантовой теории поля при попытке рассчитать эффект Казимира ^[7].

Для тех, кто захочет получить больше информации по теме отмечу, что написать данную заметку я решил после перевода соответствующей статьи на википедии ^[8], где в разделе «Ссылки» вы сможете найти массу дополнительного материала, в основном на английском языке.

Автор: Indalo

Источник ^[9]