В соседнем посте была приведена интересная задача, условие которой звучит следующим образом:
Вероятность того, что в один из двенадцати стульев зашиты бриллианты, равна 0.9. Какова вероятность найти бриллианты в двенадцатом стуле, если стулья открывают поочерёдно.
На ближайшее время позволим себе абстрагироваться от точных численных значений и положим вероятность того, что бриллианты зашиты, равной p, а количество стульев — n.
Хотите узнать правильное решение этой задачи? Добро пожаловать под кат!
Итак, начнём издалека. Прежде всего, найдём вероятность того, что бриллианты находятся в первом стуле. Используя формулу полной вероятности. находим
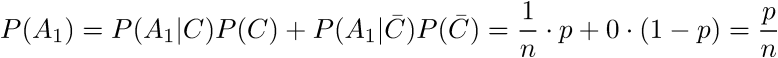
Поскольку стулья мы проверяем не одновременно, а по порядку, то второй стул мы будем вскрывать только в том случае, если в первом ничего нет:
![]()
Здесь велик соблазн раскрыть числитель получившейся дроби по правилу произведения вероятностей, однако этого делать нельзя. Мы проверяем стулья поочерёдно, а значит, наши события не являются независимыми. Поскольку бриллианты, если они были положены, могут равновероятно оказаться в любом из двенадцати стульев, то вероятность события в числителе:
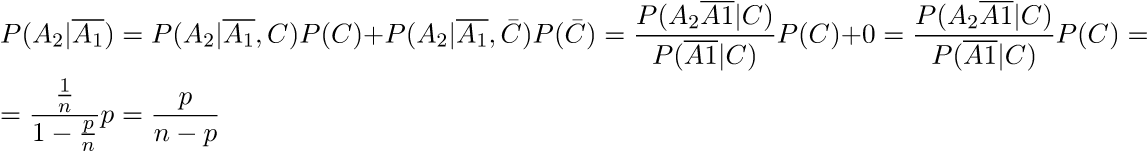
Делая новую итерацию, мы получим:
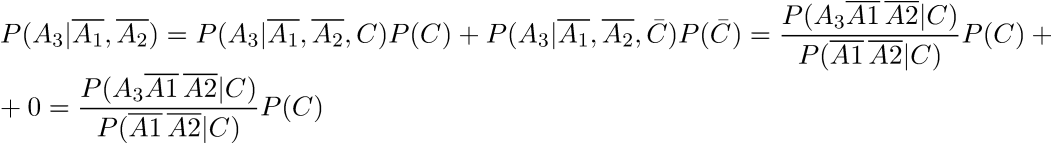
Опять же, события в знаменателе не являются независимыми, и мы не имеем право применять формулу произведения вероятностей, однако мы можем воспользоваться формулой сложения вероятностей:
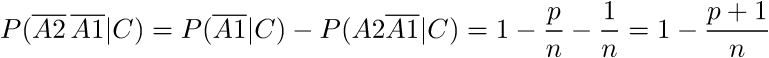
В результате мы получаем формулу:
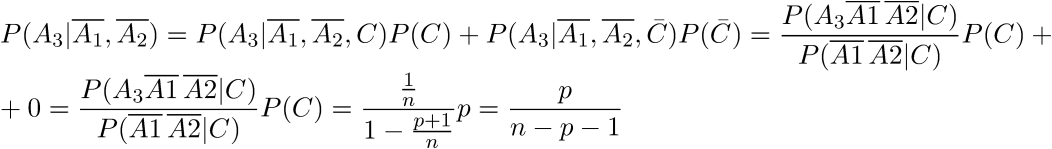
Теперь несложно видеть, что итоговая формула для вероятности того, что бриллиант зашит в k-м стуле, имеет вид:
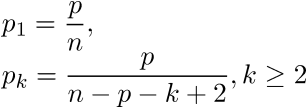
Подставляем исходные значения: p = 0.9 и n=12. В результате получаем ответ: 0.(81) или 81%.
Автор: ProPupil



