Комбинаторика в старших классах школы, как правило, ограничивается текстовыми задачами, в которых нужно применить одну из трёх известных формул — для числа сочетаний, перестановок или размещений. В институтских курсах по дискретной математике рассказывают и о более сложных комбинаторных объектах — скобочных последовательностях, деревьях, графах… При этом, как правило, ставят задачу вычислить количество объектов данного типа для некоторого параметра n, например количество деревьев на n вершинах. Узнав количество объектов для фиксированного n, можно задаться и более сложным вопросом: как все эти объекты за разумное время предъявить? Алгоритмы, решающие подобного рода задачи, называются алгоритмами комбинаторной генерации. Таким алгоритмам, например, посвящена первая глава четвёртого тома «Искусства Программирования» Дональда Кнута. Кнут очень подробно рассматривает алгоритмы генерации всех кортежей, разбиений числа, деревьев и других структур. Придумать какой-нибудь алгоритм, работающий умеренно быстро, для каждой из этих задач несложно, но с дальнейшей оптимизацией могут возникнуть серьёзные проблемы.
В процессе написания магистерской диссертации, защищённой в Академическом Университете, мне потребовалось изучить и применить один из алгоритмов комбинаторной генерации, подходящий для особого класса задач. Это генерация структур, на которых дополнительно введено некоторое отношение эквивалентности. Чтобы было понятно, о чём идёт речь, я приведу простой пример. Давайте попробуем сгенерировать все триангуляции шестиугольника. Получится что-нибудь такое:
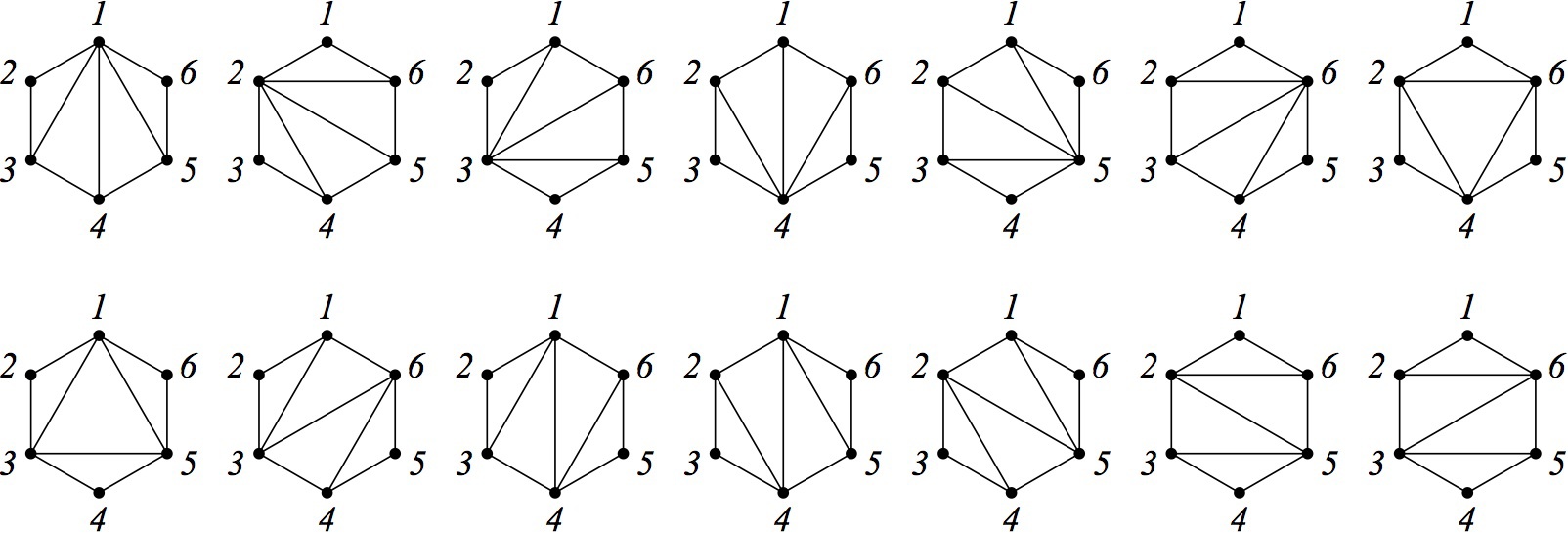
Написать алгоритм, который вернёт все такие триангуляции, довольно несложно. Например, сгодится такая процедура: фиксируем какое-нибудь ребро (пусть это будет ребро 1-6), после чего в цикле перебираем вершины, не являющиеся его концами. На текущей вершине и фиксированном ребре строим треугольник, а оставшиеся после этого две области триангулируем рекурсивно. Если присмотреться к получающимся в результате работы этого алгоритма триангуляциям, то можно заметить, что многие из них почти одинаковы и отличаются лишь тем, как расставлены пометки (номера) вершин. Поэтому, полезно было бы придумать алгоритм, который будет генерировать так называемые непомеченные триангуляции — те, что изображены на следующем рисунке:

Более формально, пусть на нашем множестве объектов действует некоторое отношение эквивалентности , разбивающее всё множество на классы изоморфных друг другу объектов. Требуется сгенерировать по одному представителю из каждого класса. Вы, наверное, заметили, что две правых триангуляции на втором рисунке тоже очень друг на друга похожи и из них можно оставить только одну. В действительности, всё зависит от того, какое отношение эквивалентности мы выбрали. Если считать изоморфными только те триангуляции, которые можно наложить друг на друга после поворота, то их останется четыре, а если разрешить ещё возможность переворачивать шестиугольник, то три.
Казалось бы, сгенерировать по одному представителю из каждого класса несложно: генерируем все объекты, после чего попарно тестируем на изоморфизм и выкидываем дубликаты. К сожалению, для некоторых типов объектов это будет работать ужасающе долго даже для небольших n. Задачу проверки изоморфизма, например, двух графов, за полиномиальное время решать не умеют, а значит, подпрограмму, решающую эту задачу, желательно вызывать как можно реже. Ещё один минус предложенного наивного подхода состоит в том, что все объекты придётся держать в памяти одновременно. При этом, если подождать медленную программу, выдающую верный ответ, ещё теоретически можно, то получить переполнение памяти вместо ответа уже совсем неприемлемо. Так что, для генерации попарно неизоморфных объектов нужно воспользоваться каким-то более хитрым методом. Такой метод неоднократно переоткрывался для многих конкретных комбинаторных объектов (графов, деревьев, разбиений), а в общем виде был описан в статье Isomorph-Free Exhaustive Generation.
Я расскажу об этом методе на примере задачи, несколько более общей по сравнению с задачей о триангуляциях: мы будем генерировать все «рассечения», то есть способы разбить многоугольник не обязательно на треугольники, а на многоугольники с числом сторон из списка, который подаётся на вход программе.
Для того, чтобы этот метод описать потребуется несколько формальных определений.
Пусть X — некоторое множество «структур». Элементы множества X мы будет называть помеченными объектами. В нашей задаче помеченными объектами являются рассечения, вершины которых пронумерованы против часовой стрелки. Структура данных для помеченных рассечений простая — это списки смежности:
public class Dissection {
private int[][] adjacent;
...
}
Пусть G — некоторая группа перестановок, действующая на множестве X. Это значит, что каждому помеченному объекту x из X и каждому элементу g группы G поставлен в соответствие другой помеченный объект y = g*x, причём выполнены следующие свойства:
- Умножению любых элементов группы h и g соответствует последовательное применение действий к объекту x: h*(g*x)=(hg)*x.
- Единица группы e переводит каждый помеченный объект x сам в себя: e*x=x.
Можно показать, что всё множество X разбивается на классы эквивалентности относительного такого отношения: x и y эквивалентны, если x=g*y. В нашем первом примере с триангуляциями, элементы группы — повороты на 0, 60, 120, 180, 240 и 300 градусов — делят всё множество на четыре класса эквивалентности, элементы которых отличаются именно своей структурой, а не пометками вершин. Эти классы эквивалентности и были изображены на втором рисунке. Мы будем называть эти классы непомеченными объектами.
Каждому элементу X мы сопоставим натуральное число, которое будем называть порядком. Порядок у всех эквивалентных объектов должен быть одинаков. Это свойство позволяет доопределить порядок для классов эквивалентности (непомеченных объектов): он будет равен порядку любого представителя соответствующего класса. Для нашего примера на рисунке, порядок — это количество вершин в многоугольнике. У всех непомеченных объектов на рисунке он равен шести.
Это были достаточно общие определения. Теперь перейдём к определениям, специфичным для будущего алгоритма. Каждому помеченному объекту x сопоставим два множества — множество нижних объектов L(x) и множество верхних объектов U(x). Порядки элементов в этих множествах по определению равны порядку x. Прежде чем дать формальные требования к нижним и верхним объектам, я попробую дать интуитивное описание. Каждый нижний объект должен содержать в себе информацию о том, как однозначно перейти от текущего объекта к объекту меньшего порядка. Например, нижний объект-рассечение — это рассечение, в котором дополнительно выделен (например, покрашен в красный цвет) один из «крайних» многоугольников, который можно от этого рассечения отрезать. Верхний объект — это, наоборот, помеченный объект плюс информация, позволяющяя его однозначным образом «нарастить», увеличив порядок. Верхнее рассечение, например, — это рассечение, в котором одна из сторон многоугольника дополнительно выделена (например, покрашена в красный цвет) и на ней написано число. Посмотрев на такое рассечение, мы можем понять, к какой стороне приклеить новый многоугольник, чтобы увеличить порядок. Число сторон приклеиваемого многоугольника будет определяться тем, какое число написано на ребре. Эту идею можно проиллюстрировать следующим рисунком, изображающим два объекта — нижний и верхний, отвечающих одному и тому же рассечению.
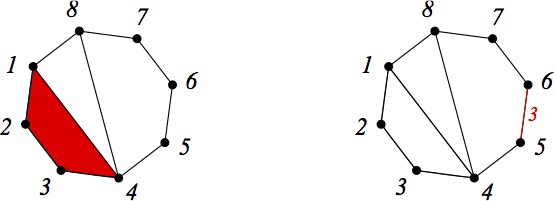
В программе нижние и верхние рассечения представлены так:
public class LowerDissection {
private Dissection dissection;
private int after;
...
}
public class UpperDissection {
private Dissection dissection;
private int after, size;
...
}
Для нижнего рассечения мы храним лишь номер вершины, с которой начинается многоугольник, который мы собираемся удалять. Для верхнего рассечения хранится номер вершины, после которой нужно будет приклеивать новый многоугольник, а так же число его сторон.
Можно заметить, что некоторые нижние и верхние объекты находятся в отношении «соответствия»: нижнему объекту соответствует верхний, получающийся после того, как мы уменьшили порядок способом, закодированным в нижнем объекте.
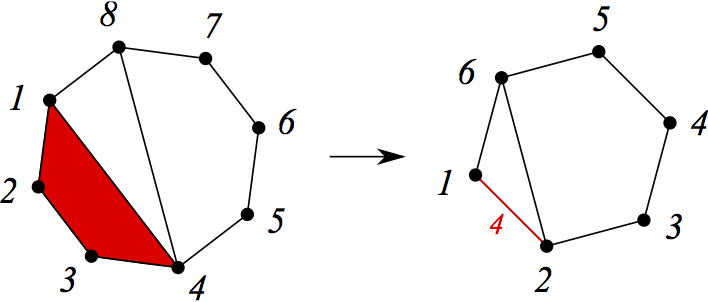
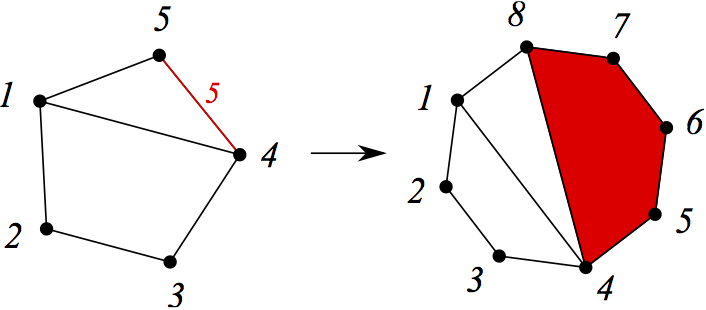
Здесь нижнему объекту сопоставляется верхний, результат удаления выделенного четырёхугольника. На следующем рисунке — наоборот: к верхнему объекту, а точнее, к его выделенному ребру с написанной на нём пятёркой, приклеивается пятиугольник. При этом получается нижний объект, хранящий информацию о том, как откатить проделанную операцию.
Теперь формально, что же нужно потребовать от упомянутых конструкций:
- Группа G действует на трёх типах объектов: помеченных, верхних и нижних. Каждое из этих трёх множеств замкнуто относительно действия группы (это значит, что, например, подействовав элементом группы на нижний объект, нельзя получить верхний — довольно формальное требование).
- Для каждого помеченного объекта x и элемента группы g: L(g*x)=g*L(x); U(g*x)=g*U(x) (запись g*L(x) значит, что мы применяем g к каждому элементу множества L(x), аналогично для g*U(x)).
- Для каждого нижнего объекта y, соответствующее ему множество верхних объектов не пусто.
- Если два нижних объекта y и x эквиваленты (то есть, y=g*x), то любые два соответствующих им верхних объекта тоже эквивалентны.
- Если два верхних объекта y и x эквиваленты, то любые два соответствующих им нижних объекта тоже эквивалентны.
- Порядок нижнего объекта больше, чем порядок любого соответствующего ему верхнего.
Чтобы лучше понять эту концепцию, предлагаю вам на минуту отвлечься от чтения и подумать, как будут выглядеть нижние и верхние объекты, если в качестве множества X взять графы без треугольников (то есть, такие графы, в которых никакие три вершины не соединены рёбрами все одновременно).
Продолжим. Пусть от некоторого непомеченного объекта нельзя ничего «откусить». Таким образом, нижних объектов, соответствующих ему (а точнее, соответствующих его помеченным объектам), нет. Такой объект называется неприводимым. В нашем случае, неприводимыми являются рассечения, состоящие из единственного многоугольника. Все остальные являются приводимыми.
Наш алгоритм будет генерировать все неизоморфные рассечения последовательно, начиная с неприводимых, постепенно наращивая их порядок. Для этого мы будем приклеивать к текущему рассечению все возможные многоугольники со всех возможных сторон. Проблема, однако, состоит в том, что к одному и тому же рассечению можно прийти несколькими способами. Например, к рассечению восьмиугольника, которому соответствовал нижний объект на двух предыдущих картинках, можно прийти, приклеив к треугольнику четырехугольник, а потом пятиугольник, а можно — приклеив, наоборот, к пятиугольнику треугольник и четырёхугольник. Таким образом, возникает возможность сгенерировать одно и то же рассечение несколько раз, и даже не заметить этого. Это то, чего как раз хочется избежать.
Чтобы обойти эту проблему, сгенерировав новое рассечение, мы будем проверять, правда ли, что последнее добавление многоугольника отвечает какому-то единственному каноническому способу построения этого рассечения. Для этого нам понадобится функция P, сопоставляющая каждому помеченному объекту множество нижних объектов, для которых он является «потомком». Функция P должна удовлетворять таким требованиям:
- Если L(x) пусто, то и P(x) тоже пусто.
- Если L(x) не пусто, то P(x) состоит из таких и только таких соответствующих объекту х нижних объектов, что любые два из них переходят друг в друга под действием какого-то элемента g, для которого g*x=x.
- Для любого непомеченного объекта x и элемента группы g: g*P(x)=P(g*x).
Стоит обратить особое внимание на второе требование: оно, фактически, означает, что множество P(x) должно состоять из нескольких объектов, являющихся эквивалентными относительно симметрий объекта x. Пусть, например, вышло так, что рассечение x симметрично относительно лишь поворотов на 0 и 180 градусов. Тогда P(x) должно состоять из ровно двух нижних объектов, получающихся друг из друга с помощью таких поворотов.
Попробуем удовлетворить общему требованию в нашем примере. Для этого возьмём какое-то рассечение x и прокрутим на нём пометки всеми n способами (n — количество вершин). Каждый раз, когда с вершин 1 и 2 будет начинаться «крайний» многоугольник (такой, что его можно отрезать), будем такую нумерацию запоминать. После этого из всего выделенного подможества нумераций вершин выберем те, которые дают лексикографически минимальную (подойдёт и любой другой разумный порядок) запись списков смежности. Эти нумерации выделяют нам некоторые многоугольники на исходном объекте х — те, которые при соответствующих нумерациях начинаются с 1 и 2. P(x) как раз и состоит из нижних объектов для x, в которых эти многоугольники покрашены в красный цвет. Без рисунка тут не обойтись:
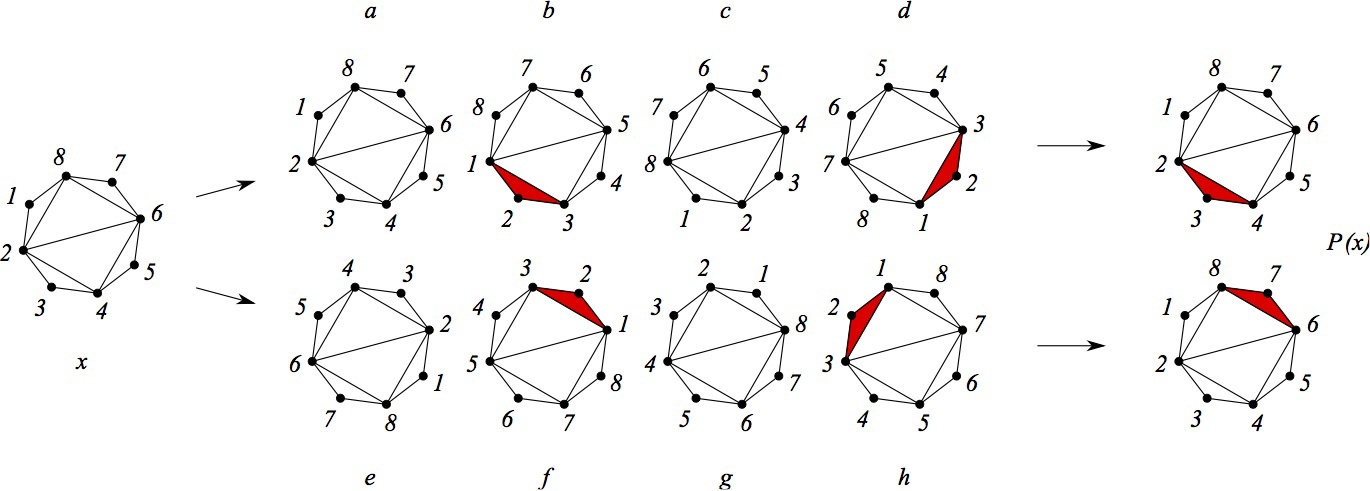
Итак, мы выбрали рассечение x, изображённое слева, и восемью различными способами переставили пометки. Способы a, c, e и g нам сразу не подходят: на вершинах 1,2,...,i не построен многоугольник, который можно отрезать. Видно, что способы b и f, в сущности, одинаковы, равно как и способы d и h. Из этих четырёх способов выбираем те, которые в некотором смысле «минимальны». Как мы уже заметили, можно определить минимум как угодно, но однозначно. Например, подойдёт минимальная лексикографически запись списков смежности. В этом случае способы b и f выигрывают. Эти способ выделяют нам треугольники 2,3,4 и 6,7,8 на исходном помеченном объекте х. В результате мы получаем два нижних объекта, показанных на рисунке справа.
Функция P — самая важная для быстрой генерации. Удовлетворить указанным требованиям и сохранить высокую скорость работы, в действительности, весьма сложно. Как видно, функция P, в некотором смысле, позволяет указать, какой из способов «откусить» крайний многоугольник является каноническим, с точностью до изоморфизма. Если концепция ясна, предлагаю вам придумать, как должна работать функция P(x) для уже упомянутых графов без треугольников.
Код, добавляющий к описанным выше классам методы, реализующие все перечисленные функции, лучше посмотреть в репозитории: в нём слишком много технических подробностей, чтобы обсуждать его в деталях.
Теперь всё готово для того, чтобы описать непосредственно алгоритм генерации. Он будет запускаться для каждого неприводимого рассечения. Для текущего рассечения мы рассматриваем все неизоморфные способы создать верхний объект, а затем каждый полученный верхний объект наращиваем до нижнего с увеличением порядка. Далее, с помощью функции P каждый нижний объект проверяем на то, что он действительно является родителем соответствующего ему помеченного объекта. Если эта проверка проходит, то считаем, что данный помеченный объект является представителем нового класса эквивалентности; запускаем алгоритм для него рекурсивно. Можно, конечно, доказать корректность этого алгоритма, но, чувствую, я и так немного переусердствовал с формализмом, да и для того, чтобы разобраться с доказательством, проще обратиться к исходной статье.
Лучше давайте вначале посмотрим на код, отвечающий за генерацию:
public static void generateSubtreeFrom(Dissection root, int maxOrder) {
for (UpperDissection upper : root.createAllUpper()) {
LowerDissection lower = upper.createArbitraryLower();
if (lower != null) {
Dissection probableChild = lower.getUnderlyingDissection();
if (probableChild.getOrder() <= maxOrder && lower.isParentFor(probableChild)) {
root.addChild(probableChild);
generateSubtreeFrom(probableChild, maxOrder);
}
}
}
}
А теперь — на результат генерации всех неизоморфных рассечений на 3,4 и 5-угольники, вплоть до порядка, равного восьми. Стрелки направлены от родителей к потомкам. Видно, что все рассечения образовали деревья, корнями которых являются неприводимые объекты.
Автор: krasko