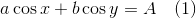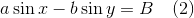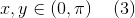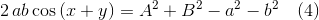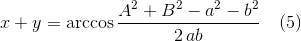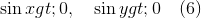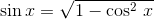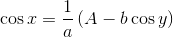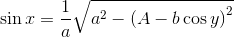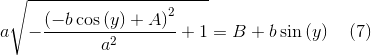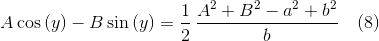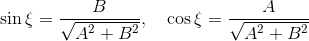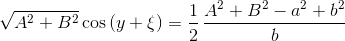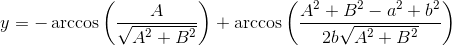Системы компьютерной алгебры: блеск, нищета или почему многие задачи не решаются «в лоб»

Введение

Системы компьютерной математики (СКА) творят чудеса. Развитие математических пакетов достигло того уровня, когда невольно закрадывается мысль — а зачем нам теперь нужны классические методики преподавания математики (или физики, или механики) в школе или вузе, если большую часть «грязной» работы по преобразованию выражений можно переложить на плечи машины. А если нельзя, или трудно получить аналитическое решение задачи, то почему бы не «прощелкать» её численно в одном из популярных пакетов. Так что, давайте ограничим уровень понимания учеников составлением исходной системы уравнений, а решать учить не будем — всё легко и непринужденно сделает за них компьютер.

Не буду скрывать, что катализатором для написания данного поста послужила статья про задачу о двух старушках, ^[1] любительницах пеших прогулок, взятая из книги В. И. Арнольда. В связи с этим, появилась мысль рассмотреть простую математическую задачу, решение которой показывает, что возможности СКА часто упираются в, довольно закономерный, верхний предел, и для получения компактного решения, пригодного для дальнейшего анализа, необходимо таки немного напрячь извилины.

1. Система тригонометрических уравнений

Когда, в не слишком далеком 2003 году я начал работать над кандидатской диссертацией, я столкнулся с необходимостью решать систему тригонометрических уравнений вида

^[2]

^[3]

причем на корни уравнения накладываются условия

^[4]

Где мы сталкиваемся с такими системами? При расчете кинематики замкнутых четырехзвенников, например. Такой замкнутый четырехзвенник был в моей работе, почти такой же попался мне около года назад, когда я взялся сделать «шабашку» (помог одному профессору в его работе).

Тогда, в 2003-м я только познакомился с системой Maple и был в восторге от её возможностей, естественно я поручил эту систему ей. И меня ждал «облом»… Посмотрим, какое решение дают Maple 18 и Mathematica 10 для этой задачи сегодня.

2. Решение задачи в СКА «в лоб»

В моем любимом Maple задаем систему уравнений

restart;

eq01 := a*cos(x) + b*cos(y) = A;
eq02 := a*sin(x) - b*sin(y) = B;

и пробуем решить

solv := solve({eq01, eq02}, {x, y});

и получаем…

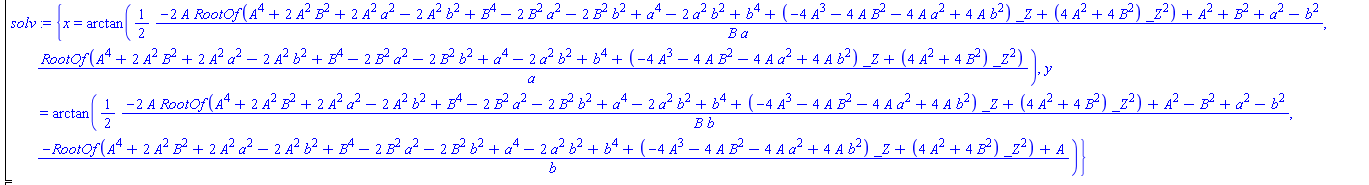
Эта бяка не влезла в онлайн-LaTeX, поэтому пришлось привести скриншот. Такой результат получается из-за того, что постановка задачи слишком общая. Необходимо указать системе, какое решение нас интересует, воспользовавшись условием (3)

solv := solve({eq1, eq2, x > 0 and x < Pi, y > 0 and y < Pi}, {x, y});

В этом случае результат выглядит получше

Ещё раз попрошу прощения у читателя за корявый скриншот и замечу, что мы получили два решения системы (1) — (3) и нам теперь ещё предстоит разобраться, какой ответ соответствует механическому смыслу задачи (он там есть, да), а учитывая, что за a, b, A и B могут таится довольно значительные выражения (не зависящие, естественно, от x и y) нам должно стать довольно грустно в этот момент.

У системы Mathematica 10 с этими уравнениями лучше дела обстоят в том смысле, что она получает конечную форму общего решения, часть которого на скрине

Если систему дополнить условием (3), то Вольфрам говорит нам, что Solve[...] не имеет метода решения для такого случая (был бы признателен читателю за подсказку по этому вопросу, ибо считаю что сам я вопрос изучил не полностью, а пока продолжу повествование).

Кроме того, обе СКА выдают в решении богомерзкий арктангенс, который не всегда удобен по разным причинам, о которых говорить не буду — в каждом случае причины свои.

Когда мой покойный ныне «шеф» увидел эти решения в 2003 году, он задумался и изрек, что «эти крокодилы надо причесать», чем заставил меня погрузится в дальнейшие раздумья. И я снова вооружился листком бумаги и карандашом…

3. СКА + головной мозг

Чтобы получить достаточно компактное решение, надо преобразовать систему (1) — (3) к линейной относительно неизвестных. Для этого надо воспользоваться школьными знаниями по тригонометрии.

Итак, возведем уравнения (1) и (2) в квадрат и сложим, перенеся всё, что не зависит от x и y в правую часть уравнения

left1 := lhs(eq01):
left2 := lhs(eq02):

right1 := rhs(eq01):
right2 := rhs(eq02):

eq03 := simplify(left1^2 + left2^2)= right1^2 + right2^2;
eq03 := eq03 - (a^2 + b^2);

left3 := combine(lhs(eq03));

eq03_1 := left3 = rhs(eq03);

используя формулу «косинус суммы», получим новое уравнение

^[5]

Теперь, разрешая его относительно суммы неизвестных приходим к линейному уравнению

^[6]

Линейное уравнение оно и в Африке линейное — найдя одну неизвестную, получим и другую. Займемся другой неизвестной, исключив x из одного их уравнений. Так как у нас есть условие (3), то очевидно, что

^[7]

а это дает нам возможность воспользоваться основным тригонометрическим тождеством без неоднозначности «плюс-минус»

^[8]

Косинус икса берем из первого уравнения

^[9]

получая, таким образом для синуса икс

^[10]

Чтобы не пыхтеть над бумагой, поручим всё это Maple

eq01_1 := subs(cos(x) = u, eq01);
slv := solve(eq01_1, u);
eq02_1 := subs(sin(x) = sqrt(1-slv^2), eq02);
eq02_1 := eq02_1 + b*sin(y);

имея на выходе уравнение

^[11]

Уравнение (7) надо возвести в квадрат и провести некоторые преобразования

left := expand(lhs(eq02_1)^2):
right := expand(rhs(eq02_1)^2):

eq02_2 := collect(simplify(right - left), b);

eq02_3 := subs(coeff(eq02_2, b) = tmp, eq02_2);

slv2 := solve(eq02_3, tmp);

eq02_4 := -2*A*cos(y) + 2*B*sin(y) = slv2;
eq02_5 := eq02_4/(-2);

придя к уравнению вида
^[12]

А теперь выполним, известный многим, «финт ушами»

left2 := lhs(eq02_5);

left3 := subs(A = O2A*cos(xi), B = O2A*sin(xi), left2);
left4 := subs(O2A = sqrt(A^2 + B^2), combine(left3));

то есть, делим обе части уравнения на 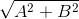^[13] и сворачиваем левую часть по формуле косинуса суммы, справедливо полагая что

^[14]

Получаем новое уравнение,

^[15]

которое успешно решаем относительно y

eq02_6 := left4 = rhs(eq02_5);
slv3 := subs(xi = arccos(A/sqrt(A^2 + B^2)), solve(eq02_6, y)):

^[16]

Как видим, игрек вышел довольно компактным. Возвращаемся к уравнению (5) и находим икс

^[17]

А теперь сравнив полученное с вышеприведенными «крокодилами», сделаем

Выводы

Системы компьютерной алгебры — незаменимый помощник современного ученого, упрощающий ему жизнь и избавляющий от необходимости зарываться в «простыни» решений на бумаге, избавляющий от досадных ошибок/описок, освобождающий мозг ^[18] для продуктивной деятельности. Но, их успешное применение неотделимо от общей математической культуры и знания элементарных вещей. Иначе, решение лежащее на почти поверхности имеет шанс не увидеть свет никогда.

Спасибо за внимание к моей писанине!

Автор: maisvendoo

Источник ^[19]