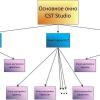
Результатом предварительной обработки речевых сигналов является получение множества спектральных векторов, характеризующих этот сигнал и используются для дальнейшего распознавания.
Принципиальное предположение, которое делается в современных распознавателях является то, что речевой сигнал рассматривается как стационарный (т.е. его спектральные характеристики относительно постоянные) на интервале в несколько десятков миллисекунд. Поэтому основной функцией предварительной обработки является разбить входной речевой сигнал на интервалы и для каждого интервала получить сглаженные спектральные оценки.
Типичная величина одного интервала — 25,6 мс. Соседние интервалы берутся со смещением относительно предыдущего интервала. Применяемая величина перекрытия интервалов равна 10 мс. В результате предварительной проработки каждого из указанных интервалов получаем вектор из нескольких десятков спектральных значений.
Блок-схема алгоритма предварительной обработки речевого сигнала приведена на Рис.1.
Шаги, которые необходимо выполнить для предварительной проработки каждого интервала речевого сигнала, подробно описаны далее.
Как пример рассматриваем речевые образцы, дискретизированные с частотою 16 КГц и с разрядностью 16 бит. Дискретизированный речевой сигнал разбиваем на интервалы длительностью 25, 6 мс, то есть 409 отсчетов. Интервалы перекрываются со сдвигом на 10 мс (160 отсчетов).
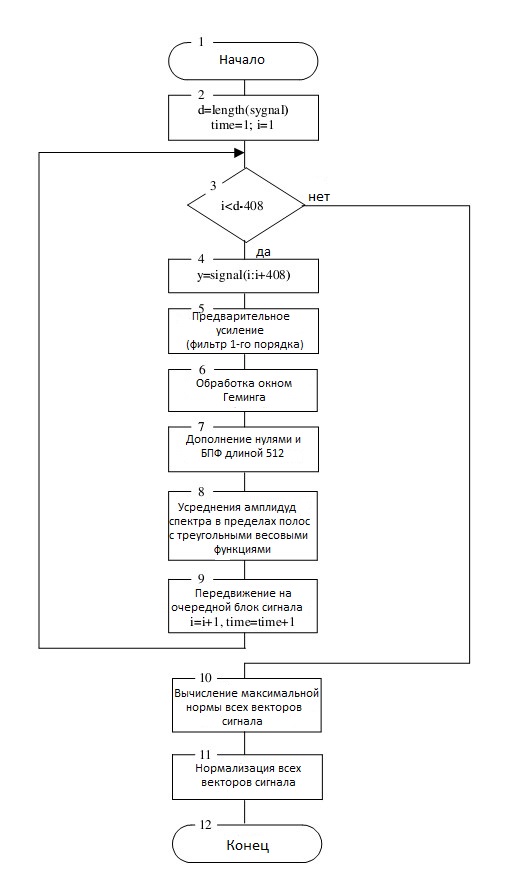
Рис.1. Блок-схема алгоритма предварительной обработки речевого сигнала
Далее этапы предварительной обработки речевых сигналов.
- Оцифрованный (дискретизированный во времени и квантованный по уровню) речевой сигнал разбиваем на блоки по 25.6 мс со смещением каждые 10 мс, то есть, блоки по 409 отсчетов каждый блок, со смещением на 160 отсчетов.
- Как правило, применяют высокочастотное усиление, чтобы компенсировать ослабление, вызвано рассеиванием от губ. Для этого блоки сигнала пропускают через фильтр первого порядка
S (1) = 0; S (n) = y (n)-y (n-1), n = 2… 409,
где yn — n-й отсчет в блоке. - Для обработок такого типа к каждому блоку применяют функцию окна.
В данном случае берется окно Геминга согласно таким выражением
D (n) = (0,54-0,46 • cos (2π • (n-1) / 408)) • S (n) для n = 1, ..., 409. - Чтобы получить спектральные оценки используется дискретное преобразование Фурье. В этом случае увеличиваем длину блока до 512 элементов за счет дополнения его справа нужным количеством нулей. После этого применяем быстрое преобразование Фурье длиной 512 точек и получаем 512 спектральных комплексных значений. Поскольку 512 значений, к которым применяем преобразование Фурье, являются действительными, то полученные спектральные комплексные значения попарно сопряжены: второе значение с 512-м, третье-с
511-м и т.д. Поэтому последние 256 комплексных значений преобразования игнорируем, потому что они комплексно сопряжены с предыдущими и не несут новой информации. - Для первых 256 комплексных спектральных значений находим их амплитуды. Амплитудный спектр Фурье сглаживается (усредняется) добавлением амплитуд спектральных коэффициентов в пределах «треугольных» частотных полос расположенных на нелинейной (подобной логарифмической) Mel-шкале. Для предельной частоты языка равной 16 КГц берут 24 таких частотных полосы.
Mel-шкала введена для приближения частотного разделения человеческого уха, которое является линейным до 1000 Гц и логарифмическим более 1000 Гц.
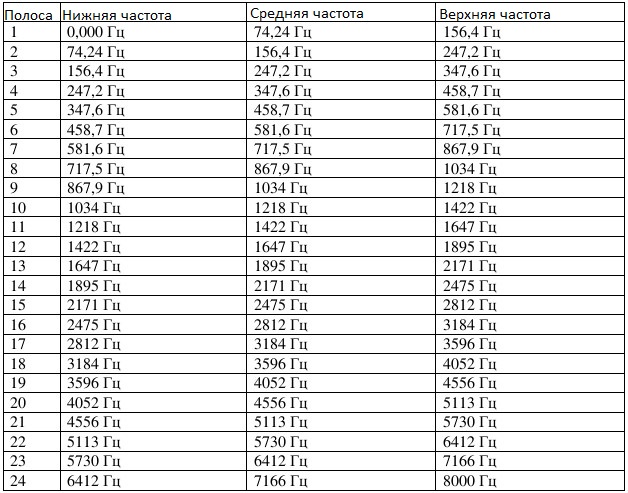
Первый амплитудный коэффициент — постоянную составляющую спектра -игнорируем, а амплитуды остальных 255 спектральных значений усредняют. Усреднения реализуем как 24 треугольные полосопропускные фильтры. Нижняя, средняя и верхняя частоты таких полос представлены в Табл.1.
Каждый треугольный фильтр находит взвешенное среднее тех амплитудных спектральных значений, соответствующих частотам в пределах между нижней и верхней частотой для данного фильтра. Если амплитуда соответствует точно средней частоте полосы, то она умножается на коэффициент равный единице. При передвижении соответствующей амплитудном значению частоты от середины к нижней или верхней границы коэффициент уменьшается от единицы до нуля.
Полученные произведения амплитуд на коэффициенты добавляются и делятся на число амплитудных значений. В результате находим взвешенное среднее для данной полосы частот.
256 амплитудам соответствуют частоты от 0 Гц до 8000 Гц, т.е. шаг передвижения равен 8000/256 = 31,25 Гц. Это означает, что первой амплитуде соответствует частота 0 Гц, второй-31,25 Гц, третьей -62,5 Гц и т.д.
Например, для первой полосы частот Mel-шкалы: нижняя частота-0 Гц, средняя частота — 74,24 Гц, верхняя частота-156,4 Гц.
Итак, в первую полосу частот попадают первые (0 Гц), вторая (31,25 Гц), третья (62,5 Гц), четвертая (93,75 Гц), пятая (125 Гц) и шестая (156,25 Гц) амплитуды.
Согласно Рис.2. третьей амплитуде соответствует коэффициент равен 62,5 / 74,24 ≈ 0,84; а пятой амплитуде — коэффициент равен (156,4-125) / (156,4-74,24) ≈ 0,38.
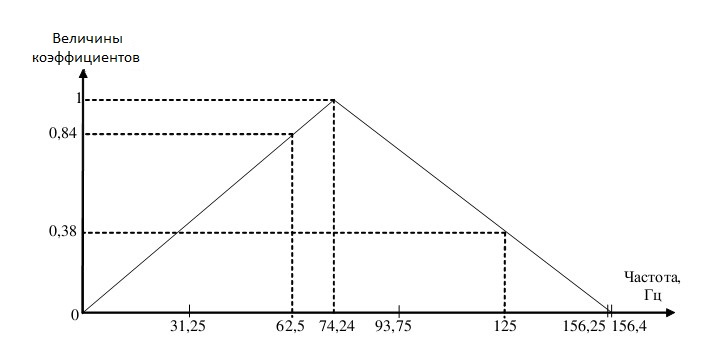
Рис.2.
Табл.1. Mel-шкала частот
В результате описанных действий получаем 24-элементный спектральный (акустический) вектор.
В заключение выполняем нормализацию акустических векторов в пределах одного языкового образца. Для этого находим наибольшую длину вектора и значения всех векторов умножаем на величину, обратную этой длины.
Для моделирования алгоритма предварительной обработки речевых сигналов выбрано среду MATLAB.
clear all;
close all;
signal = wavread('example.wav') ;
subplot(3,3,1); plot(signal);title('example.wav');
% signal: fdyscr=16 KHz, 16 bit
% acoustic preprocessing of signal
d=length(signal);
tim=1; i=1;
while i<d-408 y=signal(i:i+408); % block processing; result - acoustic vector
x(1)=0.0;
for j=2:409 x(j)=y(j)-y(j-1); end; %premphasis
% pi=3.14;
for j=1:409 z(j)=(0.54-0.46*cos(2*pi*(j-1)/408))*x(j); end; %Hamming window
C=fft(z,512); C=abs(C); % FFT
S=C(1:256); % amplitudes
% binning of 255 spectral values amplitudes, j=2,3,...,256
f=[0; 74.24; 156.4; 247.2; 347.6; 458.7; 581.6; 717.5; 867.9; 1034; 1218; 1422; 1647; 1895; 2171; 2475; 2812; 3184; 3596; 4052; 4556; 5113; 5730; 6412; 7166; 8000];
krok=16000/512; % krok=31,25
a(1:26)=0; j=2; k=1; n(1:26)=0;
h=krok*(j-1);
while k<26
while and(f(k)<h,h<f(k+1)) alfa=(h-f(k))/(f(k+1)-f(k)); % interval [f(k),f(k+1)];
a(k+1)=a(k+1)+S(j)*alfa; n(k+1)=n(k+1)+1;
a(k)=a(k)+S(j)*(1-alfa); n(k)=n(k)+1;
j=j+1; h=krok*(j-1);
end;
a(k)=a(k)/n(k); k=k+1;
end;
O(tim,1:24)=a(2:25);
%O(tim,25)=sum(y.^2);
norma(tim)=norm(O(tim,1:24));
i=i+160; tim=tim+1; % next block
end; % end of block proccesing
time=tim-1;
normamax=max(norma(1:time));
O(1:time,1:24)= O(1:time,1:24)/normamax; % normalization
% end of signal acoustic preprocessing
subplot(3,3,2); plot(y);title(' 409 values ');
subplot(3,3,3); plot(x);title(' premphasis ');
subplot(3,3,4); plot(z);title(' Hemming');
subplot(3,3,5); plot(C);title(' 512 fft ');
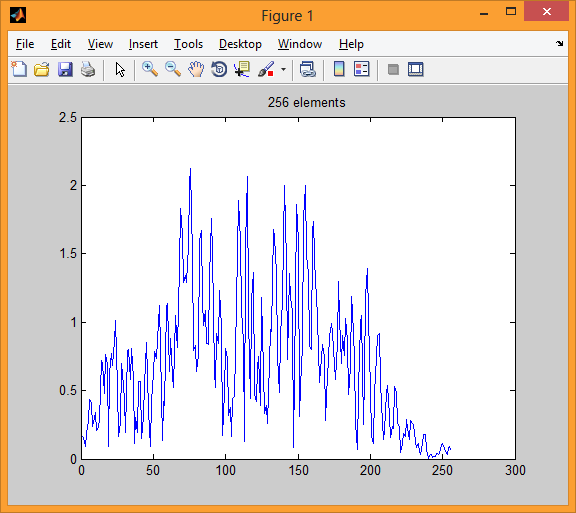
subplot(3,3,6); plot(S);title(' 256 elements ');
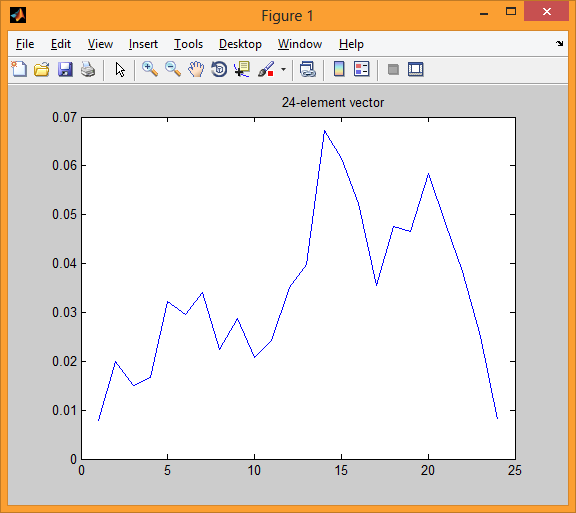
subplot(3,3,7); plot(O(time,1:24));title(' 24-element vector');
Иллюстрация этапов 1-5 предварительной обработки речевого сигнала показана на Рис.3.
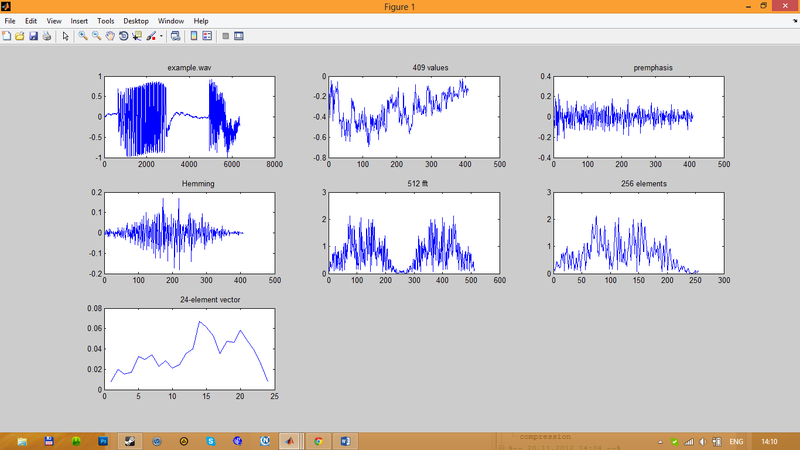
Рис.3. Этапы предварительной обработки речевого сигнала
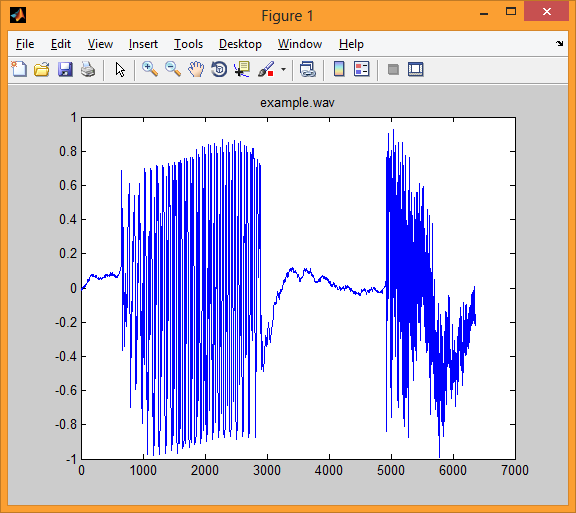
На первой иллюстрации показано языковой сигнале example.wav, Дискретизированный с частотой 16 КГц и разрядностью 16 разрядов.
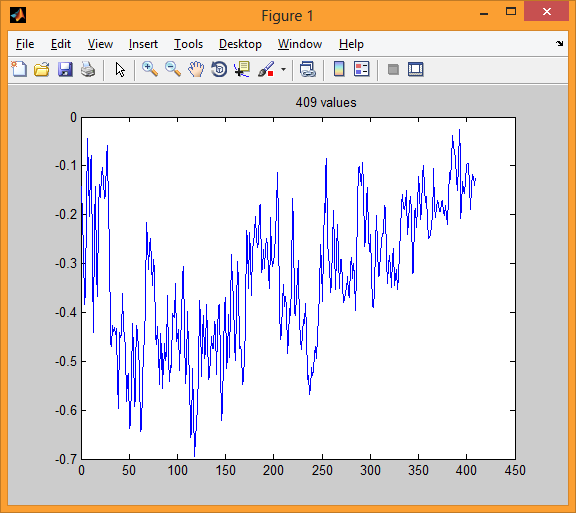
На второй иллюстрации имеем один блок (интервал) указанного речевого сигнала длительностью 25,6 мс. Такому блоку соответствует 409 отсчетов.
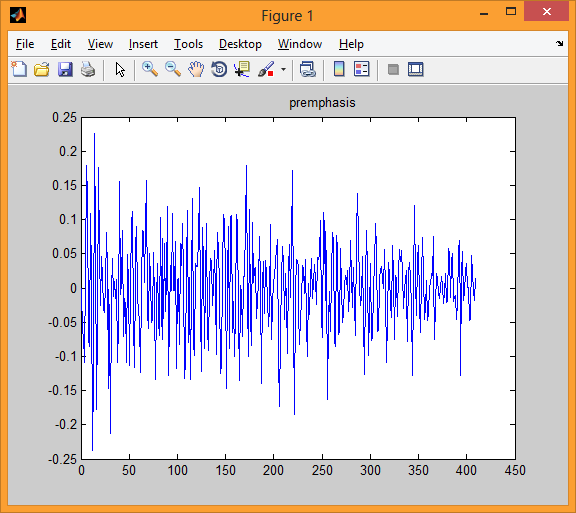
На третий иллюстрации видим один блок речевого сигнала после обработки его фильтром первого порядка.
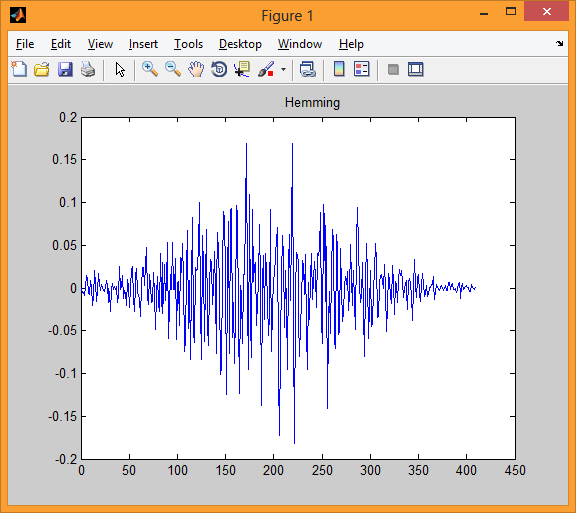
Четвертая модель показывает нам один блок после применения окна Геминга.
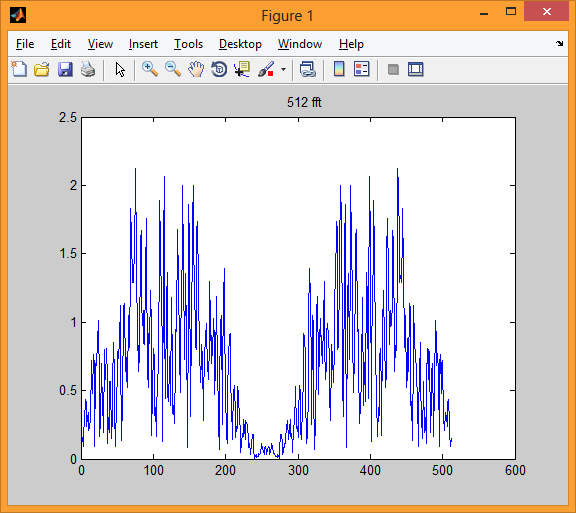
Пятая иллюстрация дает нам 512 амплитудных значений быстрого преобразования Фурье этого одного блока.
Поскольку эти амплитудные значения быстрого преобразования Фурье попарно совпадают (ибо соответствующие комплексные значения быстрого преобразования Фурье является попарно комплексно сопряженные), то можно взять только 256 первых амплитудных значений. Эти 256 амплитудных значений отражены на шестой иллюстрации.
Седьмая иллюстрация дает значение 24-элементного вектора, компоненты которого получены после усреднения 256 амплитудных значений в пределах 24 «треугольных» частотных полос.
Автор: REssential