Многие материалы по нейронным сетям сразу начинаются с демонстрации довольно сложных архитектур. При этом самые базовые вещи, касающиеся функций активаций, инициализации весов, выбора количества слоёв в сети и т.д. если и рассматриваются, то вскользь. Получается начинающему практику нейронных сетей приходится брать типовые конфигурации и работать с ними фактически вслепую.
В статье мы пойдём по другому пути. Начнём с самой простой конфигурации — одного нейрона с одним входом и одним выходом, без активации. Далее будем маленькими итерациями усложнять конфигурацию сети и попробуем выжать из каждой из них разумный максимум. Это позволит подёргать сети за ниточки и наработать практическую интуицию в построении архитектур нейросетей, которая на практике оказывается очень ценным активом.
Иллюстративный материал
Популярные приложения нейросетей, такие как классификация или регрессия, представляют собой надстройку над самой сетью, включающей два дополнительных этапа — подготовку входных данных (выделение признаков, преобразование данных в вектор) и интерпретацию результатов. Для наших целей эти дополнительные стадии оказываются лишними, т.к. мы смотрим не на работу сети в чистом виде, а на некую конструкцию, где нейросеть является лишь составной частью.
Давайте вспомним, что нейросеть является ничем иным, как подходом к приближению многомерной функции Rn -> Rn. Принимая во внимания ограничения человеческого восприятия, будем в нашей статье приближать функцию на плоскости. Несколько нестандартное применение нейросетей, но оно отлично подходит для цели иллюстрации их работы.
Фреймворк
Для демонстрации конфигураций и результатов предлагаю взять популярный фреймворк Keras, написанный на Python. Хотя вы можете использовать любой другой инструмент для работы с нейросетями — чаще всего различия будут только в наименованиях.
Самая простая нейросеть
Самой простой из возможных конфигураций нейросетей является один нейрон с одним входом и одним выходом без активации (или можно сказать с линейной активацией f(x) = x):
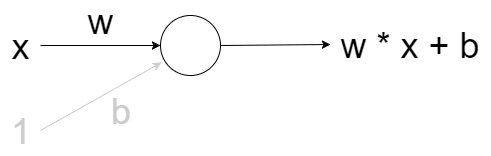
N.B. Как видите, на вход сети подаются два значения — x и единица. Последняя необходима для того, чтобы ввести смещение b. Во всех популярных фреймворках входная единица уже неявно присутствует и не задаётся пользователем отдельно. Поэтому здесь и далее будем считать, что на вход подаётся одно значение.
Несмотря на свою простоту эта архитектура уже позволяет делать линейную регрессию, т.е. приближать функцию прямой линией (часто с минимизацией среднеквадратического отклонения). Пример очень важный, поэтому предлагаю разобрать его максимально подробно.
import matplotlib.pyplot as plt
import numpy as np
# накидываем тысячу точек от -3 до 3
x = np.linspace(-3, 3, 1000).reshape(-1, 1)
# задаём линейную функцию, которую попробуем приблизить нашей нейронной сетью
def f(x):
return 2 * x + 5
f = np.vectorize(f)
# вычисляем вектор значений функции
y = f(x)
# создаём модель нейросети, используя Keras
from keras.models import Sequential
from keras.layers import Dense
def baseline_model():
model = Sequential()
model.add(Dense(1, input_dim=1, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return model
# тренируем сеть
model = baseline_model()
model.fit(x, y, nb_epoch=100, verbose = 0)
# отрисовываем результат приближения нейросетью поверх исходной функции
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True)
plt.show()
# выводим веса на экран
for layer in model.layers:
weights = layer.get_weights()
print(weights)
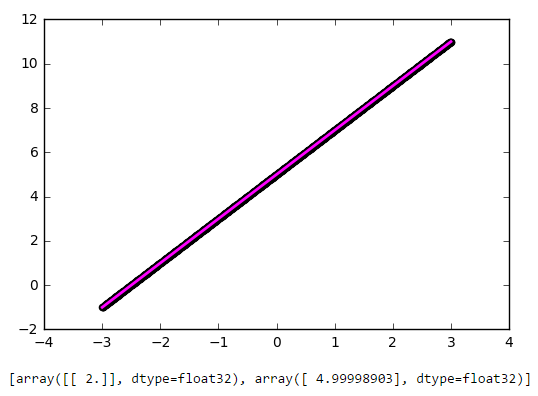
Как видите, наша простейшая сеть справилась с задачей приближения линейной функции линейной же функцией на ура. Попробуем теперь усложнить задачу, взяв более сложную функцию:
def f(x):
return 2 * np.sin(x) + 5
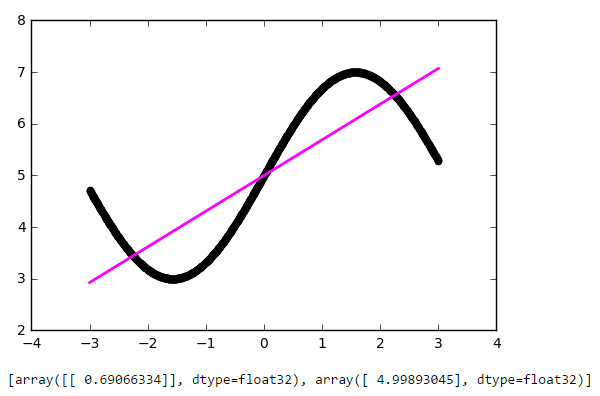
Опять же, результат вполне достойный. Давайте посмотрим на веса нашей модели после обучения:
[array([[ 0.69066334]], dtype=float32), array([ 4.99893045], dtype=float32)]
Первое число — это вес w, второе — смещение b. Чтобы убедиться в этом, давайте нарисуем прямую f(x) = w * x + b:
def line(x):
w = model.layers[0].get_weights()[0][0][0]
b = model.layers[0].get_weights()[1][0]
return w * x + b
# отрисовываем результат приближения нейросетью поверх исходной функции
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=3, antialiased=True)
plt.plot(x, line(x), color='yellow', linewidth=1, antialiased=True)
plt.show()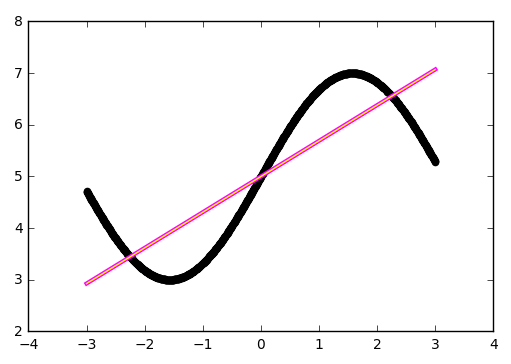
Всё сходится.
Усложняем пример
Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала. Как же захватить нейросетью нелинейность аппроксимируемой функции?
Давайте попробуем накидать побольше нейронов, скажем пять штук. Т.к. на выходе ожидается одно значение, придётся добавить ещё один слой к сети, который просто будет суммировать все выходные значения с каждого из пяти нейронов:
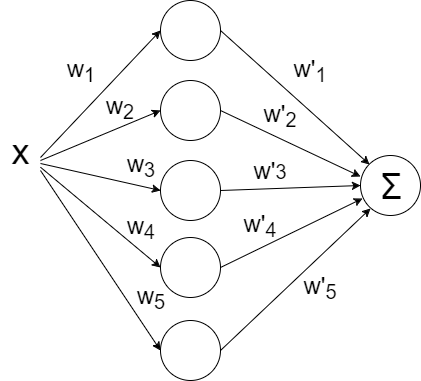
def baseline_model():
model = Sequential()
model.add(Dense(5, input_dim=1, activation='linear'))
model.add(Dense(1, input_dim=5, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return modelЗапускаем:
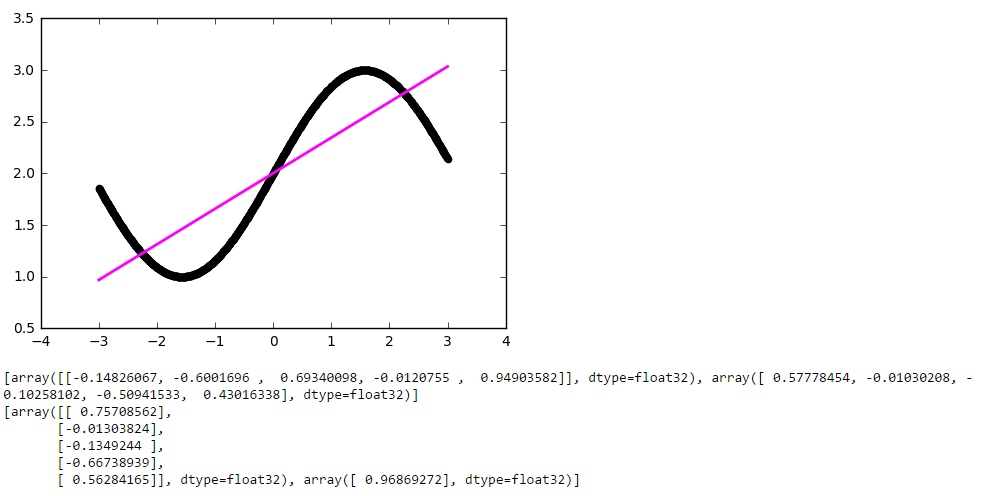
И… ничего не вышло. Всё та же прямая, хотя матрица весов немного разрослась. Всё дело в том, что архитектура нашей сети сводится к линейной комбинации линейных функций:
f(x) = w1' * (w1 * x + b1) +… + w5' (w5 * x + b5) + b
Т.е. опять же является линейной функцией. Чтобы сделать поведение нашей сети более интересным, добавим нейронам внутреннего слоя функцию активации ReLU (выпрямитель, f(x) = max(0, x)), которая позволяет сети ломать прямую на сегменты:
def baseline_model():
model = Sequential()
model.add(Dense(5, input_dim=1, activation='relu'))
model.add(Dense(1, input_dim=5, activation='linear'))
model.compile(loss='mean_squared_error', optimizer='sgd')
return model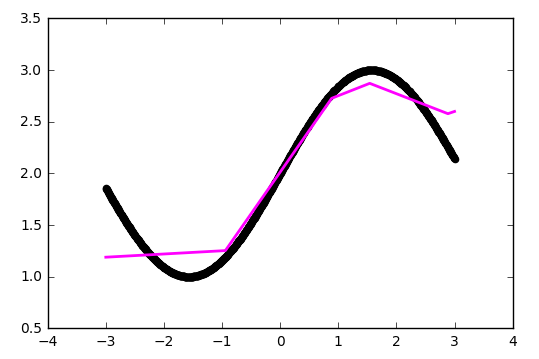
Максимальное количество сегментов совпадает с количеством нейронов на внутреннем слое. Добавив больше нейронов можно получить более точное приближение:
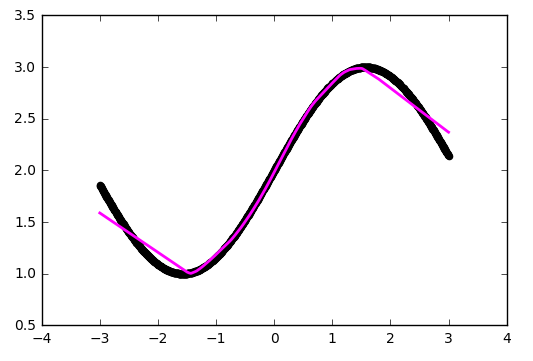
Дайте больше точности!
Уже лучше, но огрехи видны на глаз — на изгибах, где исходная функция наименее похожа на прямую линию, приближение отстаёт.
В качестве стратегии оптимизации мы взяли довольно популярный метод — SGD (стохастический градиентный спуск). На практике часто используется его улучшенная версия с инерцией (SGDm, m — momentum). Это позволяет более плавно поворачивать на резких изгибах и приближение становится лучше на глаз:
# создаём модель нейросети, используя Keras
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
def baseline_model():
model = Sequential()
model.add(Dense(100, input_dim=1, activation='relu'))
model.add(Dense(1, input_dim=100, activation='linear'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return model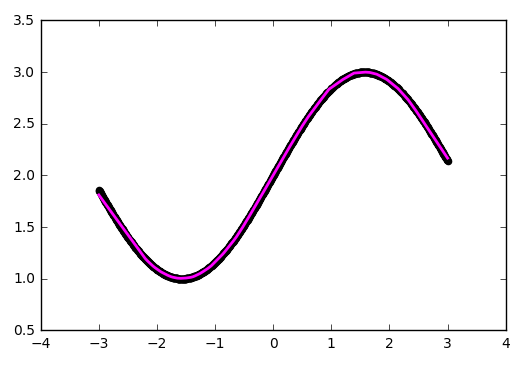
Усложняем дальше
Синус — довольно удачная функция для оптимизации. Главным образом потому, что у него нет широких плато — т.е. областей, где функция изменяется очень медленно. К тому же сама функция изменяется довольно равномерно. Чтобы проверить нашу конфигурацию на прочность, возьмём функцию посложнее:
def f(x):
return x * np.sin(x * 2 * np.pi) if x < 0 else -x * np.sin(x * np.pi) + np.exp(x / 2) - np.exp(0)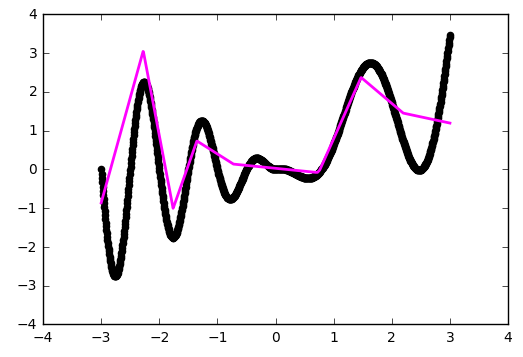
Увы и ах, здесь мы уже упираемся в потолок нашей архитектуры.
Дайте больше нелинейности!
Давайте попробуем заменить служивший нам в предыдущих примерах верой и правдой ReLU (выпрямитель) на более нелинейный гиперболический тангенс:
def baseline_model():
model = Sequential()
model.add(Dense(20, input_dim=1, activation='tanh'))
model.add(Dense(1, input_dim=20, activation='linear'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return model
# тренируем сеть
model = baseline_model()
model.fit(x, y, nb_epoch=400, verbose = 0)
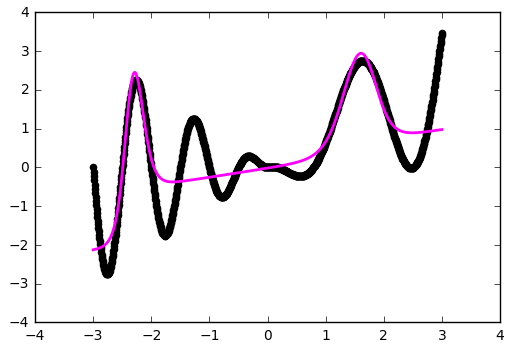
Инициализация весов — это важно!
Приближение стало лучше на сгибах, но часть функции наша сеть не увидела. Давайте попробуем поиграться с ещё одним параметром — начальным распределением весов. Используем популярное на практике значение 'glorot_normal' (по имени исследователя Xavier Glorot, в некоторых фреймворках называется XAVIER):
def baseline_model():
model = Sequential()
model.add(Dense(20, input_dim=1, activation='tanh', init='glorot_normal'))
model.add(Dense(1, input_dim=20, activation='linear', init='glorot_normal'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return model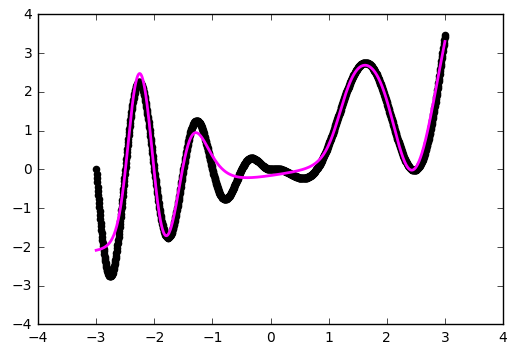
Уже лучше. Но использование 'he_normal' (по имени исследователя Kaiming He) даёт ещё более приятный результат:
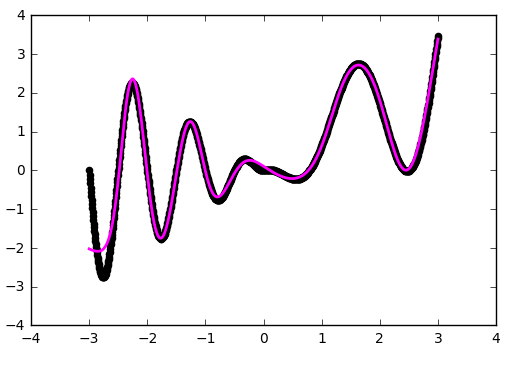
Как это работает?
Давайте сделаем небольшую паузу и разберёмся, каким образом работает наша текущая конфигурация. Сеть представляет из себя линейную комбинацию гиперболических тангенсов:
f(x) = w1' * tanh(w1 * x + b1) +… + w5' * tanh(w5 * x + b5) + b
# с помощью матрицы весом моделируем выход каждого отдельного нейрона перед суммацией
def tanh(x, i):
w0 = model.layers[0].get_weights()
w1 = model.layers[1].get_weights()
return w1[0][i][0] * np.tanh(w0[0][0][i] * x + w0[1][i]) + w1[1][0]
# рисуем функцию и приближение
plt.scatter(x, y, color='black', antialiased=True)
plt.plot(x, model.predict(x), color='magenta', linewidth=2, antialiased=True)
# рисуем разложение
for i in range(0, 10, 1):
plt.plot(x, tanh(x, i), color='blue',
linewidth=1)
plt.show()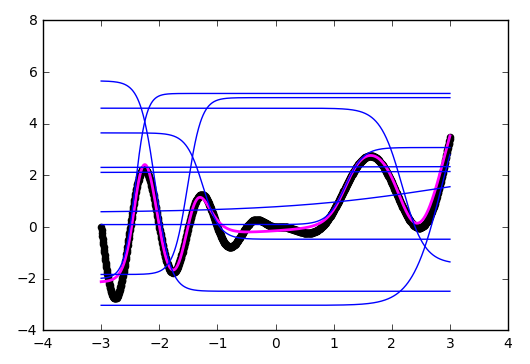
На иллюстрации хорошо видно, что каждый гиперболический тангенс захватил небольшую зону ответственности и работает над приближением функции в своём небольшом диапазоне. За пределами своей области тангенс сваливается в ноль или единицу и просто даёт смещение по оси ординат.
За границей области обучения
Давайте посмотрим, что происходит за границей области обучения сети, в нашем случае это [-3, 3]:
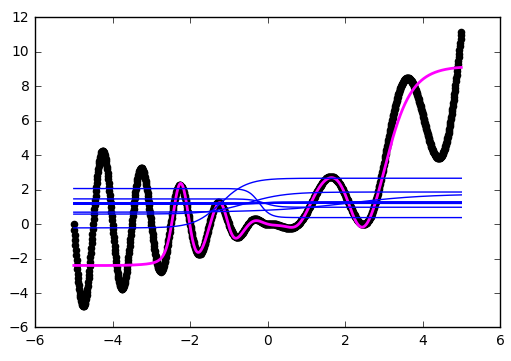
Как и было понятно из предыдущих примеров, за границами области обучения все гиперболические тангенсы превращаются в константы (строго говоря близкие к нулю или единице значения). Нейронная сеть не способна видеть за пределами области обучения: в зависимости от выбранных активаторов она будет очень грубо оценивать значение оптимизируемой функции. Об этом стоит помнить при конструировании признаков и входных данный для нейросети.
Идём в глубину
До сих пор наша конфигурация не являлась примером глубокой нейронной сети, т.к. в ней был всего один внутренний слой. Добавим ещё один:
def baseline_model():
model = Sequential()
model.add(Dense(50, input_dim=1, activation='tanh', init='he_normal'))
model.add(Dense(50, input_dim=50, activation='tanh', init='he_normal'))
model.add(Dense(1, input_dim=50, activation='linear', init='he_normal'))
sgd = SGD(lr=0.01, momentum=0.9, nesterov=True)
model.compile(loss='mean_squared_error', optimizer=sgd)
return model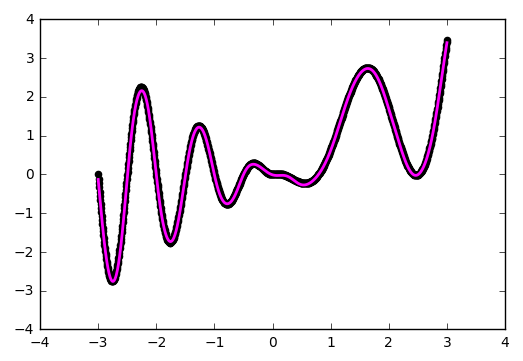
Можете сами убедиться, что сеть лучше отработала проблемные участки в центре и около нижней границы по оси абсцисс:
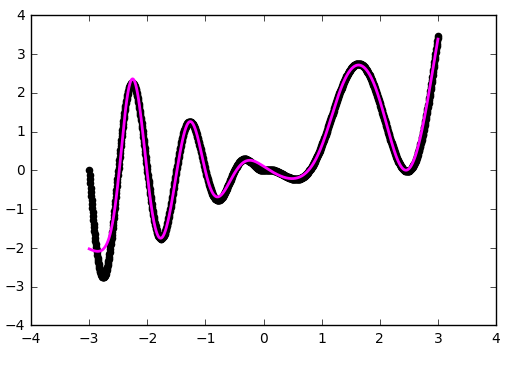
N.B. Слепое добавление слоёв не даёт автоматического улучшения, что называется из коробки. Для большинства практических применений двух внутренних слоёв вполне достаточно, при этом вам не придётся разбираться со спецэффектами слишком глубоких сетей, как например проблема исчезающего градиента. Если вы всё-таки решили идти в глубину, будьте готовы много экспериментировать с обучением сети.
Количество нейронов на внутренних слоях
Просто поставим небольшой эксперимент:
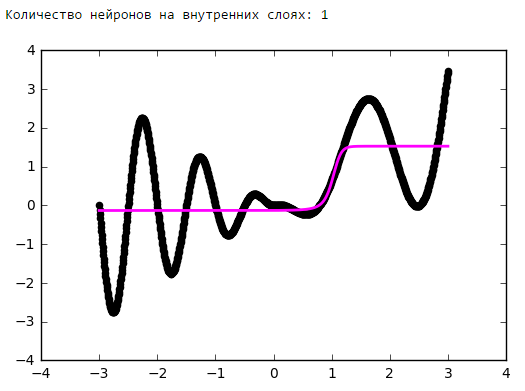
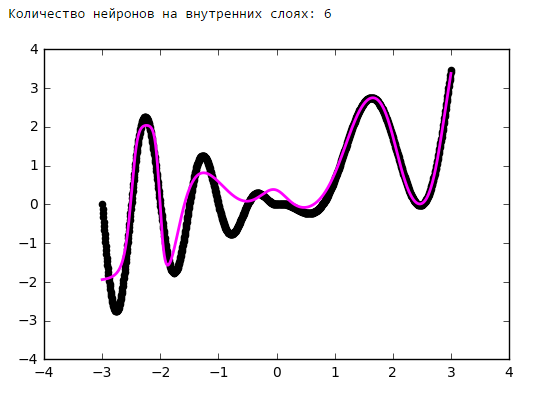
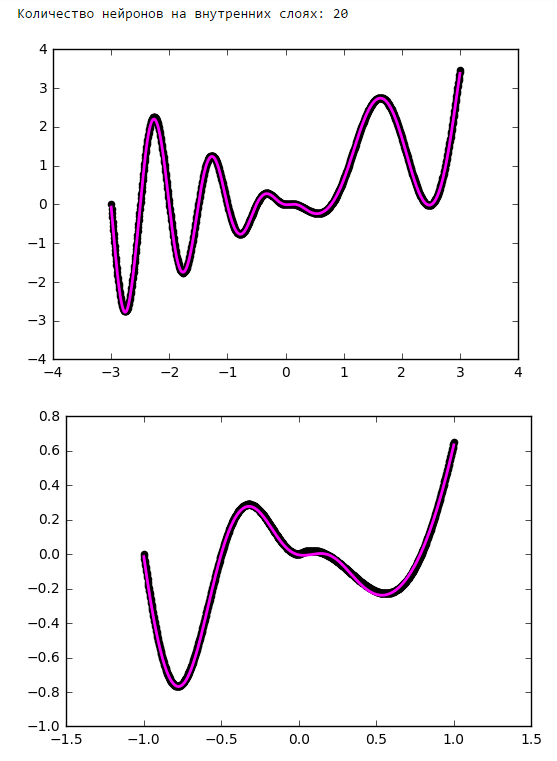
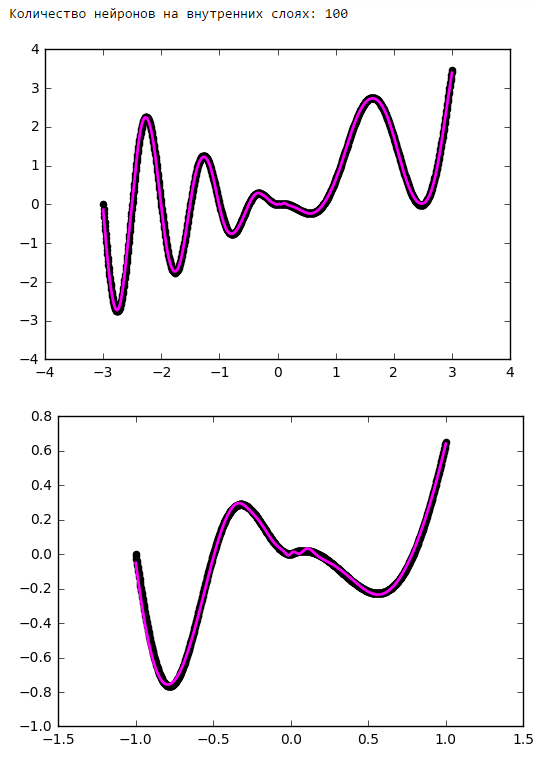
Начиная с определённого момента добавление нейронов на внутренние слои не даёт выигрыша в оптимизации. Неплохое практическое правило — брать среднее между количеством входов и выходов сети.
Количество эпох
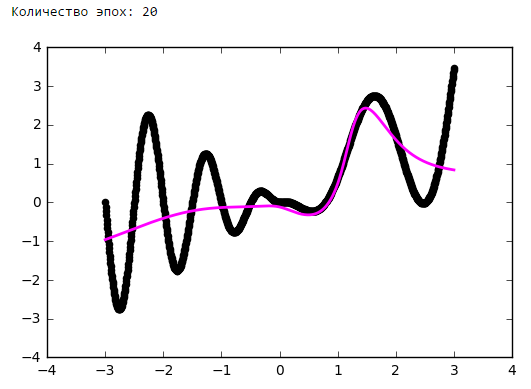
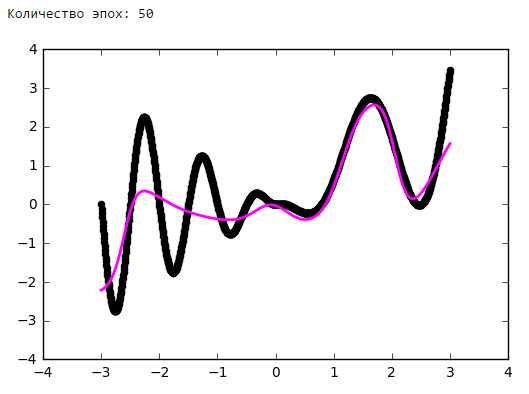
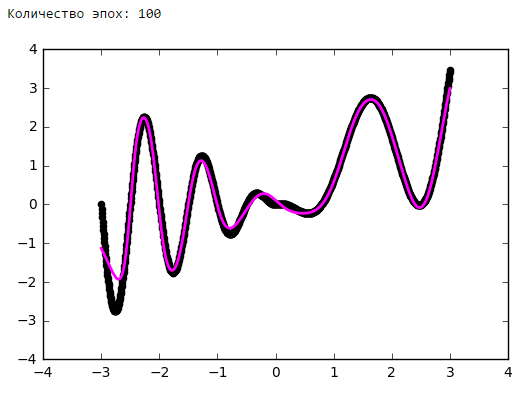
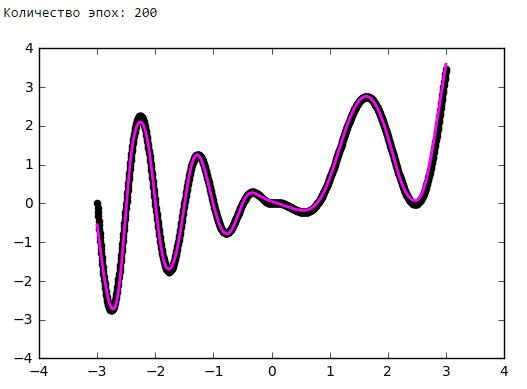
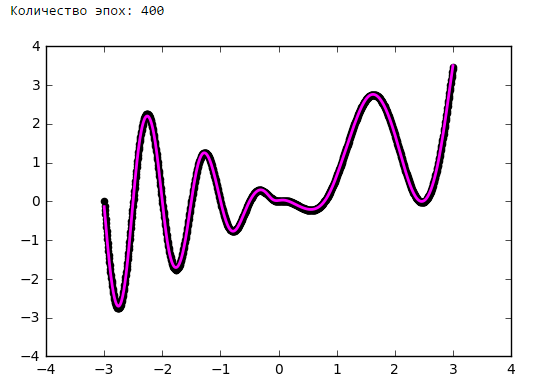
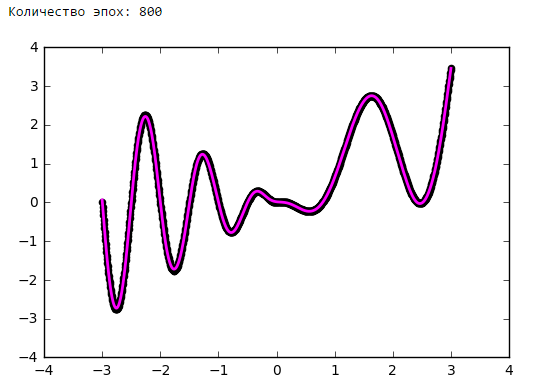
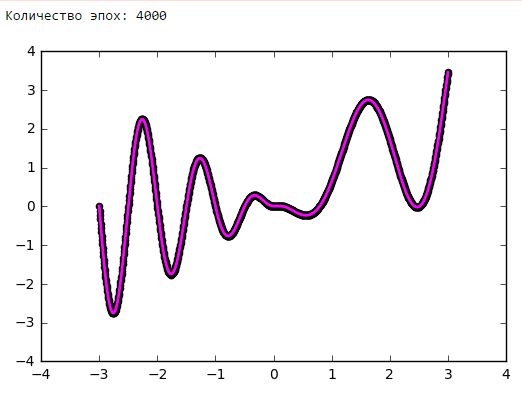
Выводы
Нейронные сети — это мощный, но при этом нетривиальный прикладной инструмент. Лучший способ научиться строить рабочие нейросетевые конфигурации — начинать с более простых моделей и много экспериментировать, нарабатывая опыт и интуицию практика нейронных сетей. И, конечно, делиться результатами удачных экспериментов с сообществом.
Автор: kdenisk



![Нейронные сети — XOR [JS] Нейронные сети — XOR [JS]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2017%2F02%2F11%2Fneironnye-seti-XOR-JS.jpg&w=100&h=100&zc=1&q=75)