Алгоритм обратного распространения ошибки с регуляризацией на c#

Привет. Я хочу продолжить тему реализации методов машинного обучения на c#, и в этой статье я расскажу про алгоритм обратного распространения ошибки для обучения нейронной сети прямого распространения, а также приведу его реализацию на языке C#. Особенность данной реализации в том, что реализация алгоритма абстрагирована от реализаций целевой функции (той, которую нейросеть пытается минимизировать) и функции активации нейронов. В итоге получится некий конструктор, с помощью которого можно поиграться с различными параметрами сети и алгоритма обучения, посмотреть и сравнить результат. Предполагается, что вы уже знакомы с тем, что такое искусственная нейросеть (если нет, то настоятельно рекомендую для начала изучить википедию или одну из подобных статей). Интересно? Лезем под кат.

Обозначения

Для начала рассмотрим обозначения, которые я буду использовать в статье, а за одно вспомним основные понятия, я не буду приводить картинок с нейронами и слоями, этого всего полно в википедии и здесь, на хабре. Итак, сразу в бой, индуцированное локальное поле нейрона (или просто сумматор) выглядит следующим образом:

• — значение линейной комбинации вектора весов и вектора входных значений, j-ого нейрона слоя n
• b — сдвиг или смещение нейрона; если условиться, что в нулевом значении входного вектора находится всегда единица , то сдвиг можно обозначить как вес с нулевым индексом, и формулу можно будет упростить
• — количество нейронов слоя n

Функция активации нейрона, или передаточная функция от значения сумматора:

• у каждого нейрона сети может быть своя функция активации
• для всех слоев кроме первого, входным вектором будет являться выходной вектор предыдущего слоя, так что

От нейрона перейдем к самой сети. Нейросеть — это модель, она обладает параметрами, и задача алгоритма обучения заключается в подборе таких параметров сети, чтобы минимизоровать значение функции ошибки. Функцию ошибки будем обозначать через E. Параметрами модели являются веса нейронов: — вес j-ого нейрона слоя n, который берет свое начало в i-ом нейроне слоя (n — 1).

Греческой эта обозначим гиперпараметр алгоритма обучения — скорость обучения.

Изменение веса обозначим через дельта:

• направление градиента показывает нам в сторону роста значения функции, но нам для минимизации необходимо двигаться в обратном направлении

Таким образом, новый вес нейрона выглядит следующим образом:
Стоит упомянуть, что к изменению веса еще можно (или, скорее, нужно) добавить регуляризацию. Функция регуляризации R — это функция от параметров модели, в нашем случае это веса нейронов. Таким образом, новая функция ошибки выглядит как E + R, а формула изменения веса преобразуется в следующую:

• лямбда — гиперпараметр обучения, коэффициент регуляризации (похож на скорость обучения)
• m — размер обучающей выборки

Вообще говоря, реализацию регуляризации тоже можно абстрагировать от алгоритма обучения, но я пока этого делать не буду, поскольку текущая реализация алгоритма обучения и так не самая быстрая, поскольку в противному случае на каждой эпохе обучения (прогон всех обучающих примеров) придется в одном цикле считать аккумулированную ошибку, а в другом — регуляризацию.Еще одна причина заключается в том, что существует не так много видов регуляризации (я, например, знаю только L1 и L2), которые применяются при обучении нейросетей. В данной реализации я буду использовать L2 норму, и она будет неотъемлемой частью алгоритма обучения.

• 
• 

Алгоритм обратного распространения ошибки

Для начала остановимся на режимах обучения. Изменять веса можно несколькими способами:

• либо после каждого обучающего примера (обучение в реальном режиме времени, online обучение, batchSize = 1)
• либо накопить изменения для всей обучающей выборки, а затем изменить все веса (full-batch, batchSize = trainingSet.Length)
• либо после прогона некоторого количества обучающих примеров (batchSize = any_number < trainingSet.Length)

Рассмотрим ситуацию с онлайн-обучением, так будет проще. Итак, на вход сети пришел импульс , сеть выдала отклик , хотя правильной реакцией на x, является .
Рассмотрим частную производную функции ошибки E:

• 
  • но так как функцию ошибки можно выразить только через сумматор, а сумматор зависит от веса, то мы можем переписать эту запись следующим образом
• 
• 
  • так вычисляется частная производная сумматора по весу, тогда можно переписать выражение частной производной целевой функции по весу; в итоге получаем
• 

Дальнейшее рассуждение разделяется на две ветки: для последнего слоя и для остальных слоев.

Выходной слой

Для выходного слоя все просто, для коррекции ошибки нам достаточно вычислить производную целевой функции по одному из весов и вычислить значение дельты. Учтем, что целевая функция полностью зависит только от выходного значения нейрона, или значения функции активации, а сама функция активации зависит только от сумматора

• 

Тут видно, что для вычисления ошибки выходного слоя нужно вычислить значение частных производных в точках, независимо от того, какая у нас целевая функция или же функция активации нейрона.

Любой скрытый слой

Но если слой не выходной, то нам нужно аккумулировать значения ошибок всех последующих слоев.

• 
  • далее учтем, что сумматор следующего слоя зависит только от выходов текущего слоя, а выходы текущего зависят только от сумматоров текущего слоя
• 
• 
  • производная сумматора по выходам предыдущего слоя выдаст нам просто вес между нейронами, учитывая это перепишем основной вывод
• 

PS: я заметил, что в верхних индексах забыл ставить скобки, чтобы обозначить, что это не степень, а индекс слоя; учтите это, пока степеней нигде не было.

Что же мы имеем:

• вычисление производной некой функции активации — это как раз то что нужно
• вычисление частной производной целевой функции по значению сумматора следующего слоя; тут тоже все просто, мы ведь находимся не на последнем слое, и вычисление изменений весов ведем от последнего к первому, так что это значение уже вычислено на предыдущем шаге
  • 
  • в случае, если следующий слой последний, то мы вычислим это значение для текущего слоя, и таким образом распространим решение на всю сеть

Реализация

Функция ошибки

С формулами покончили, давайте перейдем к реализации, и начнем с понятия функции ошибки. У меня это представлено в виде метрики (по сути, это так и есть). Метод CalculatePartialDerivaitveByV2Index вычисляет значение частной производной функции для входных векторов по индексу переменное из v2.

    public interface IMetrics<T>
    {
        double Calculate(T[] v1, T[] v2);

        /// <summary>
        /// Calculate value of partial derivative by v2[v2Index]
        /// </summary>
        T CalculatePartialDerivaitveByV2Index(T[] v1, T[] v2, int v2Index);
    }

Таким образом, мы можем вычислить значение частной производной функции ошибки для последнего слоя по реальному выходу сети .

Для примера давайте напишем несколько реализаций.

Функция активации нейрона

Аналогичным способом опишем функцию активации нейрона.

public interface IFunction
{
    double Compute(double x);
    double ComputeFirstDerivative(double x);
}

И примеры.

Нейрон, слой и сеть

В данном разделе рассмотрим представление основных элементов сети, реализацию их я приводить не буду, т.к. она очевидно. Алгоритм будет приведен для полносвязной «слоеной» сети, так что и реализацию сети нужно будет делать соответствующую.

Итак, нейрон выглядит следующим образом.

public interface INeuron
{

    /// <summary>
    /// Weights of the neuron
    /// </summary>
    double[] Weights { get; }

    /// <summary>
    /// Offset/bias of neuron (default is 0)
    /// </summary>
    double Bias { get; set; }

    /// <summary>
    /// Compute NET of the neuron by input vector
    /// </summary>
    /// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
    /// <returns>NET of neuron</returns>
    double NET(double[] inputVector);

    /// <summary>
    /// Compute state of neuron
    /// </summary>
    /// <param name="inputVector">Input vector (must be the same dimension as was set in SetDimension)</param>
    /// <returns>State of neuron</returns>
    double Activate(double[] inputVector);

    /// <summary>
    /// Last calculated state in Activate
    /// </summary>
    double LastState { get; set; }

    /// <summary>
    /// Last calculated NET in NET
    /// </summary>
    double LastNET { get; set; }

    IList<INeuron> Childs { get; }

    IList<INeuron> Parents { get; }

    IFunction ActivationFunction { get; set; }

    double dEdz { get; set; }
}

Т.к. мы рассматриваем полносвязную «слоеную» сеть, то Childs и Parents можно не имплементировать, но если делать общий алгоритм, то придется. Рассмотрим поля, которые особо важны для алгоритма обучения:

• LastNET — сумматор нейрона, тут хранится последнее вычисленное значение
• LastState — выход нейрона, тут хранится последнее вычисленное значение
• dEdz — это то самое dE/dz нейрона, что упоминается выше, и вычисляется в зависимости от того на каком слое находится текущий нейрон; частная производная функции ошибки по сумматору нейрона

Слой сети выглядит проще:

public interface ILayer
{

    /// <summary>
    /// Compute output of the layer
    /// </summary>
    /// <param name="inputVector">Input vector</param>
    /// <returns>Output vector</returns>
    double[] Compute(double[] inputVector);

    /// <summary>
    /// Get last output of the layer
    /// </summary>
    double[] LastOutput { get; }

    /// <summary>
    /// Get neurons of the layer
    /// </summary>
    INeuron[] Neurons { get; }

    /// <summary>
    /// Get input dimension of neurons
    /// </summary>
    int InputDimension { get; }
}

И представление сети:

public interface INeuralNetwork
{

    /// <summary>
    /// Compute output vector by input vector
    /// </summary>
    /// <param name="inputVector">Input vector (double[])</param>
    /// <returns>Output vector (double[])</returns>
    double[] ComputeOutput(double[] inputVector);

    Stream Save();

    /// <summary>
    /// Train network with given inputs and outputs
    /// </summary>
    /// <param name="inputs">Set of input vectors</param>
    /// <param name="outputs">Set if output vectors</param>
    void Train(IList<DataItem<double>> data);
}

Но мы рассматриваем многослойную нейросеть, так что будет использоваться особое представление:

public interface IMultilayerNeuralNetwork : INeuralNetwork
{
    /// <summary>
    /// Get array of layers of network
    /// </summary>
    ILayer[] Layers { get; }
}

Алгоритм обучения

Алгоритм обучения будет реализован через паттерн стратегия:

public interface ILearningStrategy<T>
{
    /// <summary>
    /// Train neural network
    /// </summary>
    /// <param name="network">Neural network for training</param>
    /// <param name="inputs">Set of input vectors</param>
    /// <param name="outputs">Set of output vectors</param>
    void Train(T network, IList<DataItem<double>> data);
}

Для более наглядного понимания приведу типичную функцию Train любой нейросети в контексте данной реализации:

public void Train(IList<DataItem<double>> data)
{
    _learningStrategy.Train(this, data);
}

Формат входных данных

Я использую следующий формат входных данных:

public class DataItem<T>
{
    private T[] _input = null;
    private T[] _output = null;

    public DataItem()
    {
    }

    public DataItem(T[] input, T[] output)
    {
        _input = input;
        _output = output;
    }

    public T[] Input
    {
        get { return _input; }
        set { _input = value; }
    }

    public T[] Output 
    { 
        get { return _output; }
        set { _output = value; }
    }
}

Как видно из кода в предыдущих частях, нейросеть работает с DataItem<double>.

Параметры алгоритма обучения

Данным классом описываются параметры алгоритма обучения, я думаю названия полей говорят сами за себя (и комментарии), так что не буду дублировать текстом:

public class LearningAlgorithmConfig
{

    public double LearningRate { get; set; }

    /// <summary>
    /// Size of the butch. -1 means fullbutch size. 
    /// </summary>
    public int BatchSize { get; set; }

    public double RegularizationFactor { get; set; }

    public int MaxEpoches { get; set; }

    /// <summary>
    /// If cumulative error for all training examples is less then MinError, then algorithm stops 
    /// </summary>
    public double MinError { get; set; }

    /// <summary>
    /// If cumulative error change for all training examples is less then MinErrorChange, then algorithm stops 
    /// </summary>
    public double MinErrorChange { get; set; }

    /// <summary>
    /// Function to minimize
    /// </summary>
    public IMetrics<double> ErrorFunction { get; set; }

}

Алгоритм

Ну и наконец, показав весь контекст, можно перейти к собственно реализации алгоритма обучения нейросети internal class BackpropagationFCNLearningAlgorithm : ILearningStrategy<IMultilayerNeuralNetwork>, функция public void Train(IMultilayerNeuralNetwork network, IList<DataItem<double>> data).

Для начала подготавливаем некоторые переменные (общие для всех эпох обучения) для работы алгоритма:

if (_config.BatchSize < 1 || _config.BatchSize > data.Count)
{
    _config.BatchSize = data.Count;
}
double currentError = Single.MaxValue;
double lastError = 0;
int epochNumber = 0;
Logger.Instance.Log("Start learning...");

Затем запустится основной цикл работы алгоритма, в котором происходит прямой и обратный прогон всего массива данных, один прогон называется эпохой:

do
{
//...
} while (epochNumber < _config.MaxEpoches &&
                     currentError > _config.MinError &&
                     Math.Abs(currentError - lastError) > _config.MinErrorChange);

Заходим в цикл, и перед тем как пройтись по всем примерам, инициализируем вспомогательные переменные важные только для текущей эпохи. В случае, если batch не полный, то перемешиваем данные.

lastError = currentError;
DateTime dtStart = DateTime.Now;

//preparation for epoche
int[] trainingIndices = new int[data.Count];
for (int i = 0; i < data.Count; i++)
{
    trainingIndices[i] = i;
}
if (_config.BatchSize > 0)
{
    trainingIndices = Shuffle(trainingIndices);
}

Далее наступает процесс обработки данных, в зависимости от размера пачки, и изменение весов, это выглядит так:

//process data set
int currentIndex = 0;
do
{


    //accumulated error for batch, for weights and biases
    double[][][] nablaWeights = new double[network.Layers.Length][][];
    double[][] nablaBiases = new double[network.Layers.Length][]; 

    //process one batch
    for (int inBatchIndex = currentIndex; inBatchIndex < currentIndex + _config.BatchSize && inBatchIndex < data.Count; inBatchIndex++)
    {
        //forward pass
        double[] realOutput = network.ComputeOutput(data[trainingIndices[inBatchIndex]].Input);

        //backward pass, error propagation
        //last layer
        //.......................................ОБРАБОТКА ПОСЛЕДНЕГО СЛОЯ
                        
        //hidden layers
        //.......................................ОБРАБОТКА СКРЫТЫХ СЛОЕВ
    }

    //update weights and bias
    for (int layerIndex = 0; layerIndex < network.Layers.Length; layerIndex++)
    {
        for (int neuronIndex = 0; neuronIndex < network.Layers[layerIndex].Neurons.Length; neuronIndex++)
        {
            network.Layers[layerIndex].Neurons[neuronIndex].Bias -= nablaBiases[layerIndex][neuronIndex];
            for (int weightIndex = 0; weightIndex < network.Layers[layerIndex].Neurons[neuronIndex].Weights.Length; weightIndex++)
            {
                network.Layers[layerIndex].Neurons[neuronIndex].Weights[weightIndex] -=
                    nablaWeights[layerIndex][neuronIndex][weightIndex];
            }
        }
    }

    currentIndex += _config.BatchSize;
} while (currentIndex < data.Count);

Рассмотрим обработку последнего слоя:

• инициализировали «наблЫ», там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
• пробегаемся по всем нейронам последнего слоя
• вычисляем dE/dz
• а затем вычисляем значение градиента для весов и смещения

//last layer
nablaWeights[network.Layers.Length - 1] = new double[network.Layers[network.Layers.Length - 1].Neurons.Length][];
nablaBiases[network.Layers.Length - 1] = new double[network.Layers[network.Layers.Length - 1].Neurons.Length];
for (int j = 0; j < network.Layers[network.Layers.Length - 1].Neurons.Length; j++)
{
    network.Layers[network.Layers.Length - 1].Neurons[j].dEdz =
        _config.ErrorFunction.CalculatePartialDerivaitveByV2Index(data[inBatchIndex].Output,
                                                                    realOutput, j) *
        network.Layers[network.Layers.Length - 1].Neurons[j].ActivationFunction.
            ComputeFirstDerivative(network.Layers[network.Layers.Length - 1].Neurons[j].LastNET);

    nablaBiases[network.Layers.Length - 1][j] = _config.LearningRate *
                                                network.Layers[network.Layers.Length - 1].Neurons[j].dEdz;

    nablaWeights[network.Layers.Length - 1][j] = new double[network.Layers[network.Layers.Length - 1].Neurons[j].Weights.Length];
    for (int i = 0; i < network.Layers[network.Layers.Length - 1].Neurons[j].Weights.Length; i++)
    {
        nablaWeights[network.Layers.Length - 1][j][i] =
            _config.LearningRate*(network.Layers[network.Layers.Length - 1].Neurons[j].dEdz*
                                    (network.Layers.Length > 1 ? 
                                        network.Layers[network.Layers.Length - 1 - 1].Neurons[i].LastState : 
                                        data[inBatchIndex].Input[i])
                                        +
                                    _config.RegularizationFactor *
                                    network.Layers[network.Layers.Length - 1].Neurons[j].Weights[i]
                                        / data.Count);
    }
}

Очень похоже на последний слой выглядит обработка всех скрытых слоев сети:

• пробегаемся по всем скрытым слоям
• инициализировали «наблЫ», там мы храним аккумулированное значение градиента для пачки входных данных (при онлайн обучении, там окажется просто градиент по одному примеру)
• пробегаемся по всем нейронам последнего слоя
• вычисляем dE/dz, но уже для этого мы используем значения вычисленные, на слое старше текущего
• а затем вычисляем значение градиента для весов и смещения

//hidden layers
for (int hiddenLayerIndex = network.Layers.Length - 2; hiddenLayerIndex >= 0; hiddenLayerIndex--)
{
    nablaWeights[hiddenLayerIndex] = new double[network.Layers[hiddenLayerIndex].Neurons.Length][];
    nablaBiases[hiddenLayerIndex] = new double[network.Layers[hiddenLayerIndex].Neurons.Length];
    for (int j = 0; j < network.Layers[hiddenLayerIndex].Neurons.Length; j++)
    {
        network.Layers[hiddenLayerIndex].Neurons[j].dEdz = 0;
        for (int k = 0; k < network.Layers[hiddenLayerIndex + 1].Neurons.Length; k++)
        {
            network.Layers[hiddenLayerIndex].Neurons[j].dEdz +=
                network.Layers[hiddenLayerIndex + 1].Neurons[k].Weights[j]*
                network.Layers[hiddenLayerIndex + 1].Neurons[k].dEdz;
        }
        network.Layers[hiddenLayerIndex].Neurons[j].dEdz *=
            network.Layers[hiddenLayerIndex].Neurons[j].ActivationFunction.
                ComputeFirstDerivative(
                    network.Layers[hiddenLayerIndex].Neurons[j].LastNET
                );

        nablaBiases[hiddenLayerIndex][j] = _config.LearningRate*
                                            network.Layers[hiddenLayerIndex].Neurons[j].dEdz;

        nablaWeights[hiddenLayerIndex][j] = new double[network.Layers[hiddenLayerIndex].Neurons[j].Weights.Length];
        for (int i = 0; i < network.Layers[hiddenLayerIndex].Neurons[j].Weights.Length; i++)
        {
            nablaWeights[hiddenLayerIndex][j][i] = _config.LearningRate * (
                network.Layers[hiddenLayerIndex].Neurons[j].dEdz *
                (hiddenLayerIndex > 0 ? network.Layers[hiddenLayerIndex - 1].Neurons[i].LastState : data[inBatchIndex].Input[i])
                    +
                _config.RegularizationFactor * network.Layers[hiddenLayerIndex].Neurons[j].Weights[i] / data.Count
                );
        }
    }
}

Тут основной код заканчивается, и остается сделать пару штрихов в виде вычисления средней ошибки сети на массиве данных, и логирование:

//recalculating error on all data
currentError = 0;
for (int i = 0; i < data.Count; i++)
{
    double[] realOutput = network.ComputeOutput(data[i].Input);
    currentError += _config.ErrorFunction.Calculate(data[i].Output, realOutput);
}
currentError *= 1d/data.Count;

epochNumber++;
Logger.Instance.Log("Eposh #" + epochNumber.ToString() +
                    " finished; current error is " + currentError.ToString() +
                    "; it takes: " +
                    (DateTime.Now - dtStart).Duration().ToString());

Этот блок находится прямиком перед выходом из основного цикла, продублирую код для наглядности:

} while (epochNumber < _config.MaxEpoches &&
                     currentError > _config.MinError &&
                     Math.Abs(currentError - lastError) > _config.MinErrorChange);

Итог

Собственно все. От себя хочу вот что добавить, данный текст я привел примерно в том виде, в каком я его хотел бы видеть, когда первый раз читал про алгоритм обратного распространения. Обычно в литературе авторы заранее говорят что будет использоваться такая то функция ошибки и активации нейрона. И в процессе вывода формул с частными производными они вставляют эти производные в вывод, и в итоге получается примерно так же, как, например, в википедии, где рассматривается алгоритм для минимизации квадрата Евклидова расстояния.
Вот формула для последнего слоя:

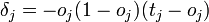
и для остальных:
.

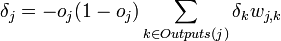Конечно, если вы очень умны, то вам не составит труда понять что тут от какого дифференциала, но я смог понять это только когда взял в руки ручку и бумагу, и написал весь вывод. Потом то же самое сделал для другой функции ошибки и только потом обобщил и осознал -)

Автор: mephistopheies