Трисекция угла и другие задачи на построение

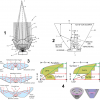
На Хабре была статья, где автор строил трисекцию угла. В этом посте я расскажу, почему невозможно точно разделить произвольный плоский угол на три равные части циркулем и линейкой, по ходу дела дам краткое введение в алгебраическую теорию полей, и покажу, как это можно применить к другим известным задачам на построение.

Введение

Знаменитая задача трисекции произвольного угла циркулем и линейкой без делений является одной из древнейших задач, привлекавших многих математиков в течение нескольких тысячелетий. Неразрешимость задачи, т.е. невозможность такого построения, была окончательно доказана в 19 веке, однако некоторые люди до сих пор предлагают свои решения. Например, решение одного академика РАН было опубликовано в журнале «Наука и жизнь». Хотя, может быть, это такой тонкий троллинг…

Наука и жизнь, №3, 1998

Правда, по словам одного профессора математики, поток писем с решениями трисекции угла и простыми доказательствами великой теоремы Ферма в последнее время заметно снизился. Сейчас ему присылают, как правило, доказательства гипотезы Римана.

Поля

В сущности, поле есть множество элементов с нулём, которые можно складывать, вычитать, умножать и делить (кроме деления на ноль) между собой, причём результат таких операций всегда однозначно определён и тоже является элементом данного поля. Кроме того, как и для арифметических операций с вещественными числами, в полях можно менять местами слагаемые/множители и раскрывать скобки без изменения результата.

Множество вещественных чисел R как раз является простейшим примером поля. При любых арифметических операциях с такими числами (кроме деления на ноль) результатом является вещественное число. Похожий пример — поле комплексных чисел C.

Поле рациональных чисел Q — это множество дробей m/n для целых m,n. Легко видеть, что при сложении/умножении/делении дробей получается дробь, поэтому Q является полем.

Множество целых чисел Z, напротив, полем не является, так как деление не всегда даёт целое число: 5/7 — нецелое, поэтому не входит в Z.

Отдельно следует отметить конечные поля, или поля Галуа — поля с конечным числом элементов. Для простого p, поле F_p можно представить как множество из p чисел {0,1,...,p-1}, в котором арифметические операции выполняются по модулю p. Например в поле F₅: 2+3=5 mod 5=0. 2*3=6 mod 5=1 и значит 1/3=(2*3)/3=2, и т.д. Конечные поля часто применяются в алгебраических помехоустойчивых кодах и криптографии: коды Рида-Соломона, AES и эллиптическая криптография оперируют в конечных полях.

Расширение поля

Поле L является расширением поля K и обозначается L/K, если L целиком содержит K, и операции в L и K действуют одинаково. К примеру, поле R является расширением R/Q поля рациональных чисел Q, а поле комплексных чисел C — расширением C/R поля R.

Рассмотрим произвольное поле K и множество K[x] всех полиномов от переменной x с коэффициентами из K. Полином p(x) из K[x] называется неприводимым над полем K, если он неразложим на (неконстантные) множители из K[x]. Например, полином P(x)=x²+1 неприводим над R, но приводим над C, т.к. разлагается на множители из C[x]: x²+1=(x-i)(x+i).

Нас будут интересовать такие расширения L/K поля K, которые можно построить, добавив к K некий элемент w (входящий в L, но не в K) и все возможные выражения с w и с элементами из K. Тогда расширение поля будем обозначать так: L/K=K(w). Если же элемент w является корнем некоего неприводимого многочлена p(x) степени d из K[x] (т.е p(w)=0), то будем писать L/K=K(w)=K[x]/(p(x)) и говорить, что L является расширением степени [L:K]=d, и w имеет степень d над полем K. В таком случае расширение L/K можно представить в виде множества полиномов с коэффициентами из K по модулю полинома p(x), т.е. множества полиномов степени ниже d. Расширения L/K первой степени равны исходному полю L=K, т.е. фактически ничуть не расширяют поле К.

Возвращаясь к примеру поля комплексных чисел: C=С/R можно получить из R присоединением мнимой единицы 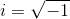C/R=R(i); при этом i является корнем неприводимого над R многочлена x²+1 (поскольку i²+1=0) второй степени, значит C=C/R=R[x]/(x²+1) является расширением степени 2, и представимо в виде множества полиномов первой и нулевой степеней с коэффициентами из R, в котором операции производятся по модулю x²+1. Или, что эквивалентно, .

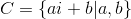Уфф. С тяжёлой теорией покончено, дальше начинается лёгкая и весёлая практика.

Построения циркулем и линейкой

Теперь зададимся вопросом, что можно и что нельзя построить с помощью циркуля и линейки?

Любое такое построение начинается с неких двух данных нам точек на плоскости, задающих единичный отрезок. Будем считать эти точки построенными. Имея две построенные точки, мы можем либо линейкой провести через них прямую, либо циркулем построить окружность с центром в одной из них и проходящую через другую. Эти прямые и окружности тоже будем называть построенными. Пересечение построенных прямых и окружностей даёт новые построенные точки, через которые можно провести новые прямые и окружности, итд. Этим исчерпываются операции с циркулем и линейкой без делений. Точки и линии являются достижимыми, если их можно построить через конечное число подобных операций.

Введём декартову систему координат 0xy, в которой исходные две точки имеют координаты (0,0) и (1,0). Допустим, числа a,b,c,d,a',b',c',d' принадлежат полю K. Можно показать, что линии, построенные на точках с такими координатами, пересекаются в точках с координатами в поле L, таком, что [L:K]≤2.

нужно показать

Прямая, проходящая через точки (a,b), (c,d), задаётся уравнением (a-c)(y-b)=(b-d)(x-a). Уравнение окружности с центром (a,b), проходящей через (c,d), задаётся (x-a)²+(y-b)²=(c-a)²+(d-b)². Коэффициенты уравнений прямых и окружностей построенных по двум парам точек (a,b), (c,d), и (a',b'), (c',d') также находятся в K. Координаты точки пересечения двух таких прямых находятся путём решения линейной системы

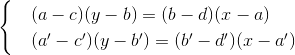
Решение выражается отношениями некоторых линейных функций коэффициентов уравнений, то есть (x,y) также принадлежит K. Координаты точки пересечения прямой и окружности берутся из системы

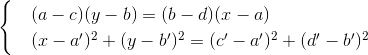
Выражая x через y из первого уравнения, подставляя и исключая x во втором, мы получаем квадратное уравнение для y с коэффициентами из K. Решение выражается через линейную комбинацию коэффициентов и корня 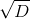из дискриминанта D уравнения. Корень уже необязательно является элементом K, но является элементом расширения 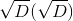. Если D не является полным квадратом в K, то мы имеем расширение второй степени, поскольку 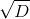есть корень неприводимого многочлена 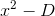. Аналогичные рассуждения для x дают 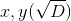. Если дискриминант отрицательный, то решения мнимые, окружность с прямой не пересекаются, и новых точек не образуется.
Наконец, для пересечения двух окружностей

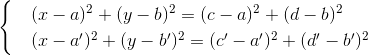
вычитаем из одного уравнения другое, сокращая x², y² и получая линейное по x,y уравнение. Добавляем новое уравнение к системе, и снова приходим к случаю пересечения прямой и окружности, в котором .

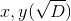Продемонстрируем эти выкладки на примере (a,b)=(0,0), (c,d)=(1,0), (a',b')=(-4/9,3), (c',d')=(1/3,1/2) с координатами из Q. Пересечения двух прямых, прямой с окружностью, двух окружностей, построенных на этих четырёх точках, имеют координаты
(x₀,y₀)=(22/45,0),
(x₁,y₁)=,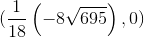
(x₂,y₂)=,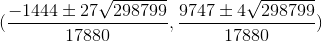
соответственно. Видно, что x₀,y₀∈Q, прямая с окружностью не пересекаются, и x₂,y₂ .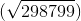

Таким образом при добавлении новой линии к нашему чертежу координаты новых построенных точек лежат в текущем поле K или в его расширении L/K степени 2. При построении же новой окружностей на точках из L/K, образуется уже расширение поля L/K: E/L, [E:L]=2. Степени последовательных расширений перемножаются, то есть E является расширением E/K поля K степени [E:K]=[E:L][L:K]=2*2=2². Значит, все достижимые точки имеют координаты из расширения поля K только степеней 2ⁿ . Построение точки (a,b) эквивалентно построению точек (a,0),(b,0), поэтому далее мы просто будем говорить «построить отрезок длиной a» или «построить число b».

Трисекция угла

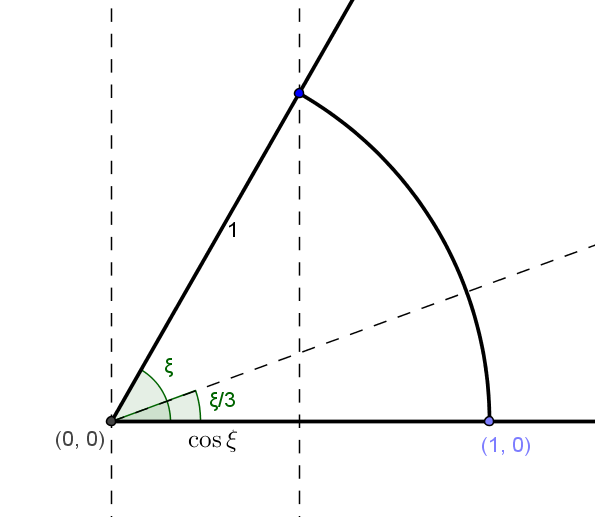
Пусть нам дана пара прямых пересекающихся под углом ξ в точке (0,0). В совокупности с другой нашей начальной точкой (1,0) задание угла эквивалентно заданию отрезка длиной cos ξ, то есть мы начинаем построение с чисел в поле Q(cos ξ). В свою очередь построение угла ξ/3 эквивалентно построению отрезка длиной cos (ξ/3). Тригонометрическое тождество cos ξ=4cos³(ξ/3)-3cos(ξ/3) показывает, что нам необходимо построить (отрезок длиной в) корень полинома p(x)=4x³-3x-cos ξ, начав с точек с координатами в поле Q(cos ξ). Однако почти для всех углов ξ данный многочлен является неприводимым над полем Q(cos ξ). Например в случае ξ=60° cos ξ=1/2 многочлен p(x)=4x³-3x-1/2 не разлагается на множители над полем Q(cos ξ)=Q(1/2)=Q. Поскольку cos(ξ/3) лежит в расширении Q(cos(ξ/3))=Q[x]/(p(x)) поля Q(cos ξ), и это расширение в случае неприводимого p(x) имеет степень полинома p(x), то есть 3≠2ⁿ, то cos(ξ/3) не является достижимой длиной отрезка или координатой точки. Следовательно, в этих случаях точная трисекция угла невозможна.

Конечно, существуют углы, допускающие трисекцию. Например, легко построить угол в 30°, имея (и даже не имея) угол в ξ=90°. В данном случае полином p(x)=4x³-3x-cos ξ=4x³-3x=x(4x²-3) разлагается на множители в Q(cos ξ)=Q; неприводимым полиномом для cos 30° является 4x²-3, расширение Q(cos(ξ/3))=Q(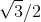) имеет степень 2 над Q, и его элементы легко достижимы циркулем и линейкой. Но таких хороших углов пренебрежимо мало.

Заключение

Похожий подход также используется в доказательствах (не)возможности других геометрических построений с циркулем и линейкой:

• Задача удвоения куба — другая неразрешимая задача древности — состоит в построении циркулем и линейкой ребра куба, объём которого вдвое больше объёма заданного куба, т.е. в построении отрезка длиной 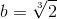при данном единичном отрезке. Легко видеть, что b является корнем неприводимого над Q многочлена x³-2, имеет степень 3≠2ⁿ над Q, и, стало быть, недостижимо.
• Аналогичная ситуация получается с квадратурой круга — задачей построения квадрата, равного по площади данному кругу. Задача сводится к построению числа 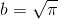, что вообще не является корнем никакого полинома из Q[x] и не имеет степени над Q.
• Построение правильного семиугольника невозможно. Оно сводится к построению чисел cos(2𝜋/7) иили sin(2𝜋/7) из поля Q. Корень седьмой степени из единицы z=e^2𝜋/7 является корнем x⁷-1=(x-1)(x⁶+x⁵+...+1) и имеет степень 6 над Q, т.к. второй множитель неприводим. С другой стороны z имеет степень 2 над L=Q(cos(2𝜋/7),sin(2𝜋/7)), поскольку z=cos(2𝜋/7)+i sin(2𝜋/7)∈L(i) и [L(i):L]=2. Следовательно, L имеет степень 6/2=3≠2ⁿ над Q и не является достижимым.
  
• Построение правильного 17-угольника, напротив, возможно, потому что z=e^2𝜋/17 является корнем x¹⁷-1=(x-1)(x¹⁶+x¹⁵+...+1) и имеет степень 16=2⁴ над Q. Вообще это работает для любого p-угольника, где p — простое число, такое что p-1=2ⁿ. Такие числа называются простыми числами Ферма. Сам Пьер Ферма утверждал, что все числа вида 2^{2^n}+1 являются простыми, верный своей привычке, бездоказательно. Впрочем, это было скоро опровергнуто. Правильный 65537-угольник, соответствующий максимальному известному простому числу Ферма, был построен Иоганном Гермесом, человеком выдающегося терпения, с помощью обычных циркуля и линейки в 1894 году.

Надеюсь, что я не слишком утомил уважаемых читателей обилием выкладок и смог на таком несложном примере продемонстрировать красоту и тесную взаимосвязанность разных разделов математики. Буду рад увидеть замечания и комментарии.

Автор: gloomsy

Источник