Снова о деревьях

Весна — пора подумать о деревьях. Деревья в DB это один из самых острых вопросов при работе с данными. В данном топике сравним быстродействие Materialized Path и Adjacency List методов с помощью команды «explain analize».

На днях я проходил собеседование в одной хорошей компании и пришел к выводу, что не все готовы изучать предмет с которым работают более досконально. А именно то что порой неявное и неправильное на первый взгляд решение может быть самым верным.

Я решил разобраться чуть более детально, в чем проблема и провести тест двух самых простых вариантов. Materialized Paths (MP) и Adjacency List (AL). Nested Sets я не рассматриваю в виду цели данного топика. А его цель, сравнить выбор parentId_parentId_parentId и выбор :pid числа.

Казалось бы, быстрее всего выбор пройдет по числу. Но рассмотрим поближе. Очень редко нам нужно выбирать отдельную ветку без наследников. Очень часто количество вложенности или просто число наследником не контролируется.

Поэтому я взял несколько разных родительских веток с вложенностью в 5 уровней по 10-30 элементов в каждом узле. Получил чуть меньше миллиона записей. Вполне рабочие цифры для не слишком активного блога, почтового клиента и т.д.

Создаем таблицу tree и индексы к ней для двух типов дерева одновременно (для чистоты эксперимента.

-- Table: public.tree

-- DROP TABLE public.tree;

CREATE TABLE public.tree
(
    id integer NOT NULL DEFAULT nextval('tree_id_seq'::regclass),
    name text COLLATE pg_catalog."default",
    pid integer,
    btree integer[]
);


-- Index: btree_idx

-- DROP INDEX public.btree_idx;

CREATE INDEX btree_idx
    ON public.tree USING gin
    (btree);

-- Index: pid_idx

-- DROP INDEX public.pid_idx;

CREATE INDEX pid_idx
    ON public.tree USING btree
    (pid);

Наиболее внимательные заметили странное поле btree. Мы говорим абстрактно, а на делаем оптимизировано.

Итак мы создали условное дерево, два поля для разных методов и уникальный идентификатор. Добавляем в него данные к примеру так:

// Generate ...
func (c *TreeController) Generate() {

    for i := int64(0); i < 10; i++ {
        pidStr := ""
        cur_i_id, _ := c.GenerateRecurse(0, pidStr)
        for j := 0; j < 30; j++ {
            pidStr := strconv.Itoa(int(cur_i_id))
            cur_j_id, _ := c.GenerateRecurse(cur_i_id, pidStr)
            for z := 0; z < 10; z++ {
                pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id))
                cur_z_id, _ := c.GenerateRecurse(cur_j_id, pidStr)
                for z1 := 0; z1 < 10; z1++ {
                    pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id)) + "," + strconv.Itoa(int(cur_z_id))
                    cur_z1_id, _ := c.GenerateRecurse(cur_z_id, pidStr)
                    for z2 := 0; z2 < 10; z2++ {
                        pidStr := strconv.Itoa(int(cur_i_id)) + "," + strconv.Itoa(int(cur_j_id)) + "," + strconv.Itoa(int(cur_z_id)) + "," + strconv.Itoa(int(cur_z1_id))
                        c.GenerateRecurse(cur_z1_id, pidStr)
                    }
                }
            }
        }
    }
}

// GenerateRecurse ...
func (c *TreeController) GenerateRecurse(pid int64, treepid string) (int64, error) {

    v := models.Tree{
        Name:  "test -- " + treepid,
        Pid:   pid,
        Btree: "{" + treepid + "}"}
    return models.AddTree(&v)
}

Здесь я намеренно не хотел замарачиваться с рекурсиями, потому написал так. Изначально хотел рекурсивно сделать, а потом подумал, что это тема для отдельного топика, и оставил как есть.

Запросы я выполнил проще. Открыл pgAdmin4 и запустил EXPLAIN ANALYZE с включенным Cost и timing флагами.

А интересовали нас два запроса.

Для MP:

SELECT * FROM tree
WHERE btree && ARRAY[:pid]
ORDER BY array_length(btree, 1);

Для AL:

WITH RECURSIVE nodes(id,name,pid, btree) AS (
    SELECT s1.id, s1.name, s1.pid, s1.btree
    FROM tree s1 WHERE pid = :pid
        UNION
    SELECT s2.id, s2.name, s2.pid, s2.btree
    FROM tree s2, nodes s1 WHERE s2.pid = s1.id
)
SELECT * FROM nodes
order by pid asc;

Где :pid — id родителя.

Запрос для AL метода весьма и весьма запутанный. А этот запрос придется достаточно часто использовать.

Из результата я уберу сортировку, она выполняется в обоих запросах сопоставимое время, причем достаточно большое, и без него результат будет более впечатлителен.

Вот красивые картинки:

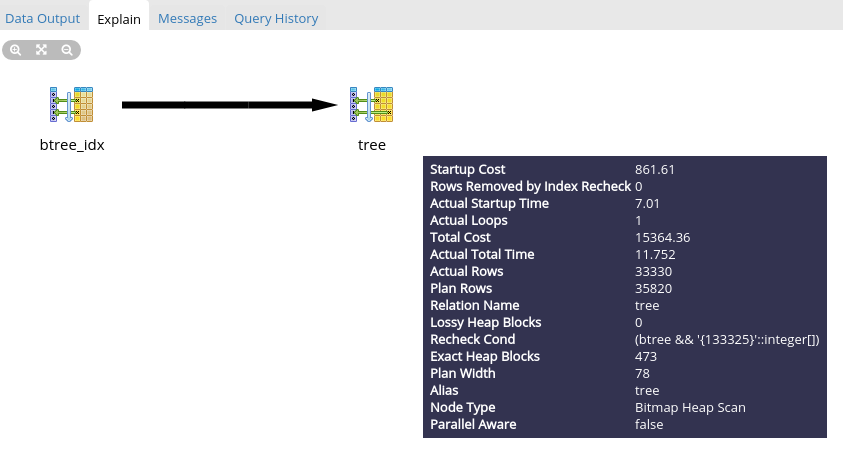
Как то все просто, но это для MP. Смотрим запрос для AL:

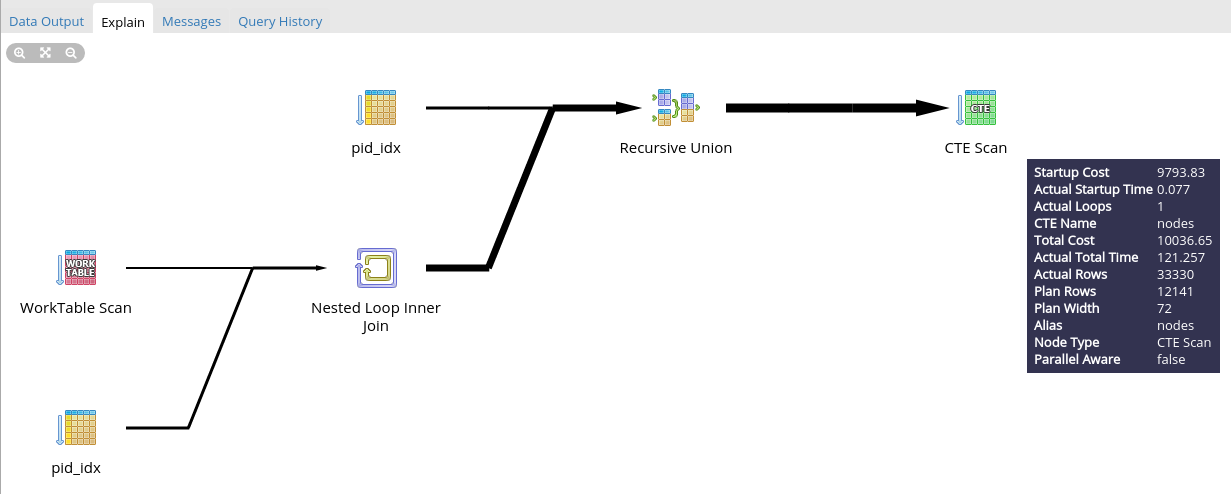
Уже красивее, но смотрим, что Total Cost у MP в полтора раза больше… А все потому что у нас индекс хранит не числа а массив чисел. Но не смотря на это в результате скорость выполнения у MP на порядок выше. И чем больше вложенностей и количество родительских элементов, том больше разница в скорости.

Кроме того простота выборки из запросов с легкостью позволяют собирать данные через ORM систему одним запросом. Большим минусом MP является более сложный метод переноса данных из одной ветки в другую, но тем не менее достаточно прозрачный. А такие операции как правило не носят массового характера и акцентировать внимание на это не совсем верно при такой разнице в производительности.

На скриншотах все данные актуальные, это не пиковые значения, а вполне средние. Но даже в пиковых значениях разница в скорости не менее 5 раз (самый медленный MP и самый быстрый AL метод.

Согласитесь, весьма неплохой бонус для тех кто хочет действительно во всем разобраться.

Автор: Игорь

Источник